标签:tty 计算过程 class c# arp type write math minus
最近学习机器学习 才发现以前数学没有学好 开始从线性代数开始学起 读完行列式一章写了些C#的代码学习一下。
直接上C#代码:
using System;
using System.Collections.Generic;
using System.Linq;
using System.Text;
using System.Runtime.InteropServices;
using System.IO;
namespace LYF.Math
{
///
/// 行列式 Determinant
///
[SerializableAttribute]
[ComVisibleAttribute(true)]
public class Determinant where T : IComparable, IFormattable, IConvertible, IComparable, IEquatable
{
T[,] tarr = null;
public Determinant(int n)
{
tarr = new T[n, n];
}
public Determinant(T[,] arrT)
{
if (arrT == null || arrT.GetLength(0) != arrT.GetLength(1) || arrT.GetLength(0)
/// 获取元素值
///
///
///
///
public T this[int i, int j]
{
//实现索引器的get方法
get
{
return GetItem(i, j);
}
//实现索引器的set方法
set
{
SetItem(i, j, value);
}
}
///
/// 获取元素的余子式
///
///
///
///
public Determinant A(int i, int j)
{
if (N == 1)
{
return null;
}
else if (i>N||j>N)
{
return null;
}
else
{
Determinant a = new Determinant(N - 1);
for (int m = 1; m = i)
{
p = m + 1;
}
if (q >= j)
{
q = n + 1;
}
a[m, n] = this[p,q];
}
}
return a;
}
}
///
/// 设置行列式的值
///
/// 行数(从1开始)
/// 列数(从1开始)
/// 值
public void SetItem(int i, int j, T value)
{
if (tarr == null)
{
throw new MathException("行列式未正确初始化");
}
else if (i > N || j > N)
{
throw new MathException("超出行列式索引范围");
}
else
{
tarr[i - 1, j - 1] = value;
}
}
public void SetItem(T[,] arrT)
{
if (arrT == null || tarr == null)
{
throw new MathException("不能为空");
}
else if (arrT.GetLength(0) != N || arrT.GetLength(1) != N)
{
throw new MathException("传入阶数不同");
}
else
{
for (int m = 0; m
/// 设置行列式的值
///
/// 行数(从1开始)
/// 列数(从1开始)
/// 值
public T GetItem(int i, int j)
{
if (tarr == null)
{
throw new MathException("行列式未正确初始化");
}
else if (i > N || j > N)
{
throw new MathException("超出行列式索引范围");
}
else
{
return tarr[i-1, j-1];
}
}
///
/// 输出行列式信息
///
///
public override string ToString()
{
StringBuilder sbRs = new StringBuilder();
if(tarr!=null)
{
for (int m = 0; m
/// 获取行列式的阶数
///
public int N
{
get{
if (tarr != null)
{
return tarr.GetLength(0);
}
else
{
return 0;
}
}
}
private string typeName = string.Empty;
private string GetType()
{
if (string.IsNullOrEmpty(typeName))
{
typeName=typeof(T).Name;
File.AppendAllText("E:\\op.txt", typeName);
}
return typeName;
}
///
/// 获取行列式的值
///
public T Value
{
get
{
if (N == 1)
{
return tarr[0, 0];
}
else if (N == 2)
{
return Minus(MUL(tarr[0, 0], tarr[1, 1]), MUL(tarr[0, 1], tarr[1, 0]));
}
else
{
T sum = default(T);
for (int i = 1; i
/// 加法
///
///
///
///
private T Add(T left, T right)
{
switch (GetType())
{
case "Int16":
return ((T)(object)((short)(object)left + (short)(object)right));
case "Int32":
return ((T)(object)((int)(object)left + (int)(object)right));
case "Int64":
return ((T)(object)((long)(object)left + (long)(object)right));
case "Single":
return ((T)(object)((float)(object)left + (float)(object)right));
case "Double":
return ((T)(object)((double)(object)left + (double)(object)right));
case "Decimal":
return ((T)(object)((decimal)(object)left + (decimal)(object)right));
}
throw new MathException("不支持的操作类型");
}
///
/// 减法
///
///
///
///
private T Minus(T left, T right)
{
switch (GetType())
{
case "Int16":
return ((T)(object)((short)(object)left - (short)(object)right));
case "Int32":
return ((T)(object)((int)(object)left - (int)(object)right));
case "Int64":
return ((T)(object)((long)(object)left - (long)(object)right));
case "Single":
return ((T)(object)((float)(object)left - (float)(object)right));
case "Double":
return ((T)(object)((double)(object)left - (double)(object)right));
case "Decimal":
return ((T)(object)((decimal)(object)left - (decimal)(object)right));
}
throw new MathException("不支持的操作类型");
}
///
/// 乘法
///
///
///
///
private T MUL(T left, T right)
{
switch (GetType())
{
case "Int16":
return ((T)(object)((short)(object)left * (short)(object)right));
case "Int32":
return ((T)(object)((int)(object)left * (int)(object)right));
case "Int64":
return ((T)(object)((long)(object)left * (long)(object)right));
case "Single":
return ((T)(object)((float)(object)left * (float)(object)right));
case "Double":
return ((T)(object)((double)(object)left * (double)(object)right));
case "Decimal":
return ((T)(object)((decimal)(object)left * (decimal)(object)right));
}
throw new MathException("不支持的操作类型");
}
}
}
以上代码就是对行列式的封装 可以求值获得余子式 很基本的东西 求值的话主要用了递归的方式 因为泛型的原因导致计算过程重复拆箱装箱 不过目前好像也没有什么太好的方法了。反正就是学习 所以性能无所谓了。
然后就是调用了直接上调用代码:
int[,] aaa = new int[4, 4]{{1,2,3,6},
{4,5,7,8},
{7,8,9,10},
{3,8,4,3}};
//LYF.Math.Determinant d = new Determinant(4);
LYF.Math.Determinant d = new Determinant(aaa);
d.SetItem(aaa);
Console.WriteLine("当前行列式:");
Console.WriteLine(d.ToString());
Console.WriteLine("余子式M11:");
Console.WriteLine(d.A(1, 1).ToString());
Console.WriteLine("余子式M12:");
Console.WriteLine(d.A(1, 2).ToString());
Console.WriteLine("余子式M22:");
Console.WriteLine(d.A(2, 2).ToString());
Console.WriteLine("N="+d.N);
Console.WriteLine("行列式的值为:"+d.Value.ToString());
Console.Read();
执行结果如下:
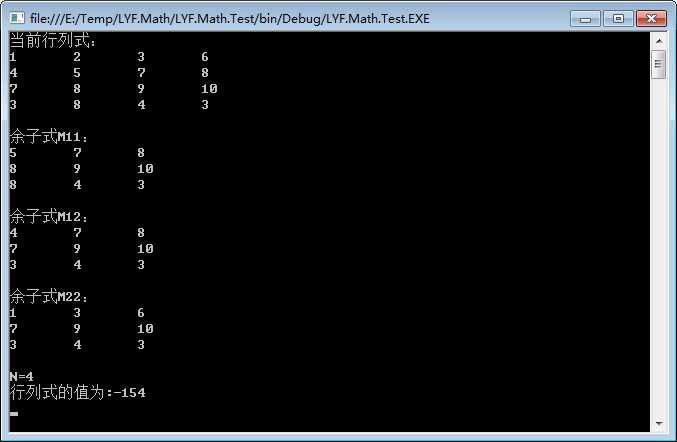
线性代数之行列式的C#研究实现
标签:tty 计算过程 class c# arp type write math minus
原文地址:http://www.cnblogs.com/devgis/p/7874305.html
