树状数组的应用及拓展
2021-05-04 19:28
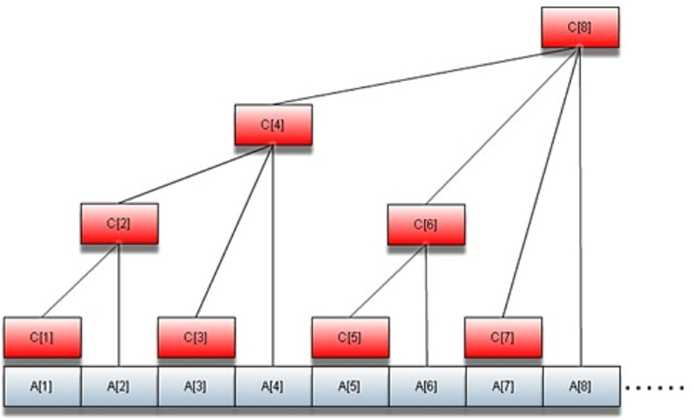
标签:前缀数组 树状 nbsp lowbit font mic str img mamicode 众所周知,树状数组是一个常用的数据结构。。。 1.为啥用树状数组: 如果用普通的前缀数组来维护前缀的信息,即使查询时o(1)的,但是修改就几乎要o(n),效率有时十分低下. 而树状数组却弥补了这一缺点,修改和查询都是o(logn)的 2.如何构建树状数组: 根据二次幂的性质,我们可以把一个数转化成一个独一无二的二进制数,所以,我们可以建立一个类似于二进制数的数组来维护前缀和 假如一个整数 x可以别分为x=2^i1+2^i2+2^i3...+2^im那么就可以把一个区间[1...x]分为(logx)的几个小区间 假设i1>i2>i3>...im 1长度为2^i1区间[1,2^i1] 2长度为2^i2区间[2^i1+1,2^i1+2^i2] 3长度为2^i3区间[2^i2+2^i1+1,2^i1+2^i2+2^i3] ... 这些小区间的特点是长度为二进制分解下最小的二次幂,也就是lowbit(x); 例如11=8+2+1=2^3+2^1+2^0,那么区间11可以分为[1,8],[9,10],[11],长度分别为lowbit(8)=8,lowbit(10)=2,lowbit(11)=1 树状数组的应用及拓展 标签:前缀数组 树状 nbsp lowbit font mic str img mamicode 原文地址:https://www.cnblogs.com/cwjr/p/13189517.html
下一篇:数组求和:二分递归