java实现二叉树
2021-05-06 19:30
阅读：426
1）在二叉树的第i层上最多有2i-1 个节点 。（i>=1）
2）二叉树中如果深度为k,那么最多有2k-1个节点。(k>=1）
3）n0=n2+1 n0表示度数为0的节点数，n2表示度数为2的节点数。
4）在完全二叉树中，具有n个节点的完全二叉树的深度为[log2n]+1，其中[log2n]是向下取整。
5）若对含 n 个结点的完全二叉树从上到下且从左至右进行 1 至 n 的编号，则对完全二叉树中任意一个编号为 i 的结点有如下特性：
2）二叉树中如果深度为k,那么最多有2k-1个节点。(k>=1）
3）n0=n2+1 n0表示度数为0的节点数，n2表示度数为2的节点数。
4）在完全二叉树中，具有n个节点的完全二叉树的深度为[log2n]+1，其中[log2n]是向下取整。
5）若对含 n 个结点的完全二叉树从上到下且从左至右进行 1 至 n 的编号，则对完全二叉树中任意一个编号为 i 的结点有如下特性：
(1) 若 i=1，则该结点是二叉树的根，无双亲, 否则，编号为 [i/2] 的结点为其双亲结点;
(2) 若 2i>n，则该结点无左孩子， 否则，编号为 2i 的结点为其左孩子结点；
(3) 若 2i+1>n，则该结点无右孩子结点， 否则，编号为2i+1 的结点为其右孩子结点。
二、二叉树的实现
（1）增加节点
二叉树是有序的，所以增加节点遵循以下规则：
1 如果新节点小于当前的值，我们将会进入左子树
2 如果新节点大于当前的节点。我们将会进入右子树
3 当前的节点是null时，我们已经到达叶子节点，我们 可以添加新节点到这个位置
具体代码如下，采用递归的形式（相同节点不能插入）
//增加节点
public Node addNode(Node current,int data) {
if(current==null) {
return new Node(data);
}
if(datacurrent.data) {
current.left=addNode(current.left,data);
}else if(data>current.data) {
current.right=addNode(current.right,data);
}else {
return current;
}
return current;
}
（2）删除节点
删除节点首先要分为以下几种情况：
1、删除的是叶子节点，找到当前节点父节点，判断当前节点是父节点
左孩子还是右孩子，然后父节点左孩子或右孩子变为空
2、删除的节点有一个孩子（左孩子或右孩子），以左孩子为列，找到当前节点父节点，判断当前节点是父节点 的左孩子还是右孩子，然后父节点左孩子指向当前节点左孩子即可。
3、删除的节点有两个孩子，一般找到被删除节点的前驱或者后继节点，然后替换被删除节点。以前驱节点为列（当前节点左孩子中最右的孩子，即最大的节点）：
（1）前驱节点就是当前节点左孩子，
(2）前驱节点不是当前节点左孩子，一般要找到前驱节点的父节点（因为替换的时候，前驱节点的父节点左或右置为空）
(a)如图删除的是叶子节点：
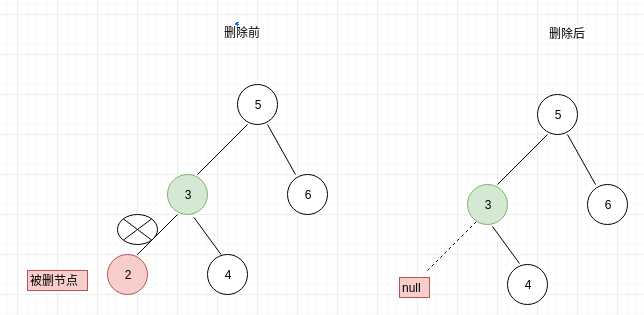
（b)删除节点有一个孩子，以左孩子为列，如图：
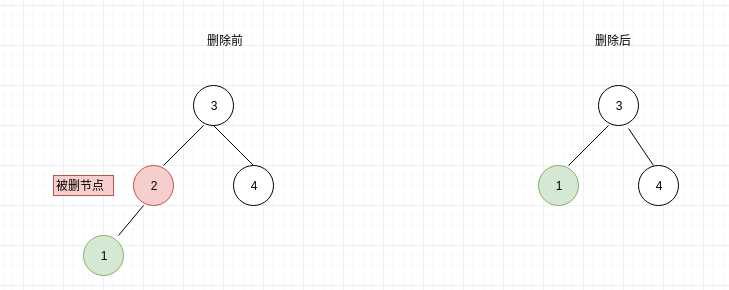
(c)删除节点有2个孩子为列。注意前驱节点、后继节点是哪一个。前驱节点是被删除节点左孩子中最大的那个节点（左孩子中最右的节点），后继节点是被删除节点有孩子中最小的节点（最左的）
如下图：前驱节点所处位置
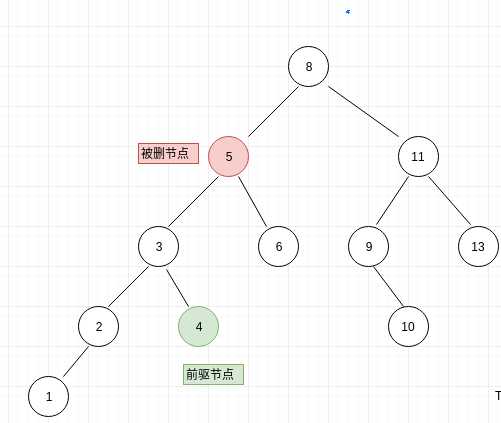
删除规则：就是找到前驱节点替换被删除节点，前提的找到 被删节点父节点、左右孩子、是否是父节点左孩子，
前驱节点的父节点（替换后要前驱节点原先位置变为null)、以及前驱节点是否是父节点左孩子。
(c1)、还有一种就是前驱节点就是当前节点左孩子，则不需要找前驱节点父节点啥的，直接将3替换5的位置，如下图：
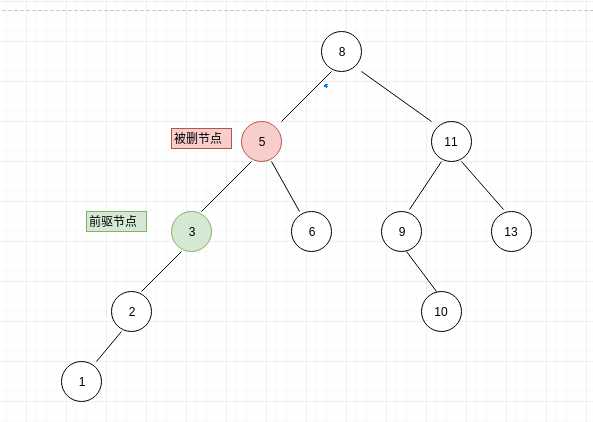
（c2)前驱节点不是当前节点（被删节点）左孩子，则需要找到前驱节点父节点、是否是左孩子，因为要把前驱节点原来位置变为前驱节点的左孩子，因前驱节点左孩子为null
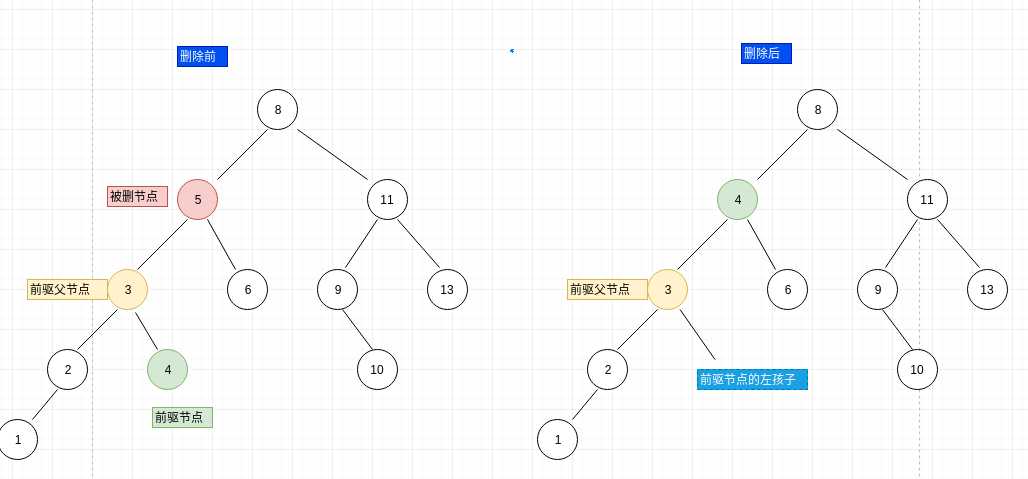
源码如下：
//删除一个节点 public void remove(int data) { Node current = null,parent = null; Node p=root; boolean isLeft=true;//当前节点是否是父节点的左孩子 while(p!=null) { if(datap.data) { parent=p; p=p.left; isLeft=true; }else if(data>p.data) { parent=p; p=p.right; isLeft=false; }else { current=p; break; } } //删除节点是叶子节点 if(current.left==null&¤t.right==null) { if(isLeft) { parent.left=null; }else { parent.right=null; } }else if(current.left!=null&¤t.right==null) { //删除节点有一个左孩子 if(isLeft) { parent.left=current.left; }else { parent.right=current.left; } }else if(current.left==null&¤t.right!=null) { //删除节点有一个右孩子 if(isLeft) { parent.left=current.right; }else { parent.right=current.right; } }else if(current.left!=null&¤t.right!=null) { //删除节点有2个孩子， 一般找到改节点前驱或者后继替换该节点 前驱：该节点左孩子中最大的节点 后继：该节点右孩子中最小的节点，以前驱为列 Node leftCurrent=current.left; Node rightCurrent=current.right;//找到前驱节点，使前驱节点替换被删节点（即当前节点）右孩子指向该节点（rightCurrent） Node preNode=null;//前驱节点 Node preLeftNode=null;//前驱节点左孩子（前驱节点只能有左孩子或者左孩子为空） Node preParentNode = null;//前驱节点父节点 Node q=current.left; //当前节点左孩子没有孩子 那前驱节点就是当前节点左孩子（前驱节点父节点就是当前节点，即被删除节点，preParentNode=null） if(q.right==null) { preNode=q; preParentNode=null; preLeftNode=preNode.left;//说明当前节点左孩子就是前驱节点，所以要把删除的节点左孩子置为空，因为这个节点要替换当前节点（被删除） //执行删除操作 首先把当前节点父节点指向前驱节点，然后把前驱节点父节点右孩子变为null,isLeft当前节点是左孩子还是右孩子 if(isLeft) { parent.left=preNode; preNode.right=rightCurrent; preNode.left=preLeftNode; }else { parent.right=preNode; preNode.right=rightCurrent; preNode.left=preLeftNode; } }else { if(q!=null) { preParentNode=q; preNode=q.right; preLeftNode=preNode.left; q=preNode.right; } //执行删除操作 首先把当前节点父节点指向前驱节点，然后把前驱节点父节点右孩子变为null,isLeft当前节点是左孩子还是右孩子 if(isLeft) { parent.left=preNode; preNode.right=rightCurrent; preNode.left=leftCurrent; }else { parent.right=preNode; preNode.right=rightCurrent; preNode.left=leftCurrent; } //前驱节点父节点右孩子变为前驱节点的左孩子 if(preParentNode!=null) { preParentNode.right=preLeftNode; } } } }
（3）二叉树的遍历，前序遍历（根、左、右）、中序遍历（左、根、右）、后续遍历（左、右、根）
//前序遍历
public void preTraversal(Node current) {
if(current!=null) {
System.out.println(current.data);
preTraversal(current.left);
preTraversal(current.right);
}
}
//中序遍历
public void inTraversal(Node current) {
if(current!=null) {
preTraversal(current.left);
System.out.println(current.data);
preTraversal(current.right);
}
}
//后序遍历
public void postTraversal(Node current) {
if(current!=null) {
preTraversal(current.left);
preTraversal(current.right);
System.out.println(current.data);
}
}
（4）二叉树的查找
//查找一个节点
public Node search(Node current,int data) {
if(current==null) {
return null;
}
if(data==current.data) {
return current;
}
return datasearch(current.left, data):search(current.right,data);
}
（5） 主要测试操作
创建如下二叉树：
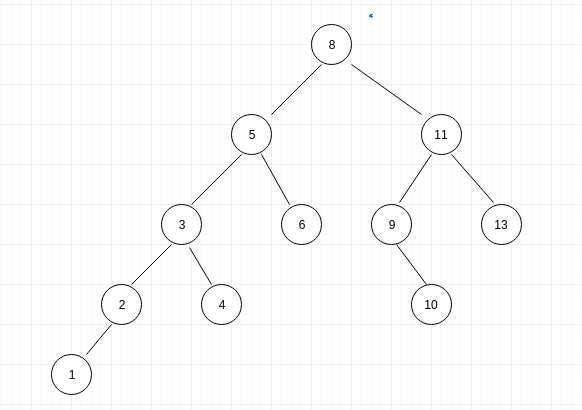
（a)增加节点：
public static void main(String[] args) {
BinaryTree bt=new BinaryTree();
bt.addNode(8);
bt.addNode(5);
bt.addNode(11);
bt.addNode(3);
bt.addNode(6);
bt.addNode(9);
bt.addNode(13);
bt.addNode(10);
bt.addNode(2);
bt.addNode(4);
bt.addNode(1);
//前序遍历
bt.preTraversal(bt.root);
}
(b)前序遍历结果如下，
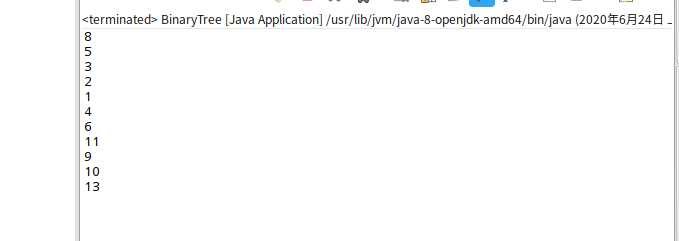
（c)、删除1（叶子节点），前序遍历结果如下：
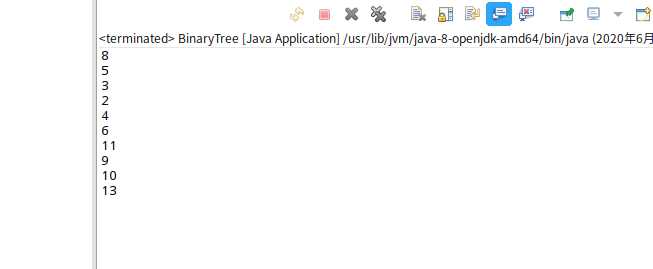
（d)、删除3节点（前驱节点就是被删节点左孩子），前序遍历如下：
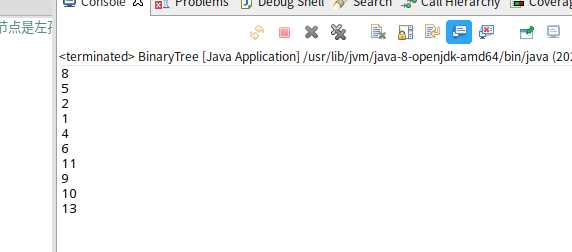
（e)删除5节点（前驱节点不是被删节点的左孩子），前序遍历如下:
（6）代码自己测试过，不足之处还请大家指出。
评论
亲，登录后才可以留言！