C++-PTA-6-7-1 地下迷宫探索
标签:存储结构 生活 战争 ++ 才智 UNC alt lis 方式
6-7-1 地下迷宫探索
我们在回顾前辈们艰苦卓绝的战争生活的同时,真心钦佩他们的聪明才智。在现在和平发展的年代,对多数人来说,探索地下通道或许只是一种娱乐或者益智的游戏。本实验案例以探索地下通道迷宫作为内容。
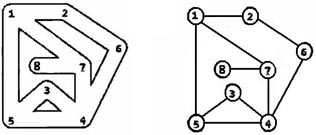
假设有一个地下通道迷宫,它的通道都是直的,而通道所有交叉点(包括通道的端点)上都有一盏灯和一个开关。请问你如何从某个起点开始在迷宫中点亮所有的灯并回到起点?
输入格式:
输入第一行给出三个正整数,分别表示地下迷宫的节点数N(1,表示通道所有交叉点和端点)、边数M(≤,表示通道数)和探索起始节点编号S(节点从1到N编号)。随后的M行对应M条边(通道),每行给出一对正整数,分别是该条边直接连通的两个节点的编号。
输出格式:
若可以点亮所有节点的灯,则输出从S开始并以S结束的包含所有节点的序列,序列中相邻的节点一定有边(通道);否则虽然不能点亮所有节点的灯,但还是输出点亮部分灯的节点序列,最后输出0,此时表示迷宫不是连通图。
由于深度优先遍历的节点序列是不唯一的,为了使得输出具有唯一的结果,我们约定以节点小编号优先的次序访问(点灯)。在点亮所有可以点亮的灯后,以原路返回的方式回到起点。
输入样例1:
6 8 1
1 2
2 3
3 4
4 5
5 6
6 4
3 6
1 5
输出样例1:
输入样例2:
6 6 6
1 2
1 3
2 3
5 4
6 5
6 4
输出样例2:
构造无向图,邻接表DFS,节点小优先(栈)
选择邻接表还是邻接矩阵存储图
根据邻接表和邻接矩阵的结构特性可知,当图为稀疏图、顶点较多,即图结构比较大时,更适宜选择邻接表作为存储结构。当图为稠密图、顶点较少时,或者不需要记录图中边的权值时,使用邻接矩阵作为存储结构较为合适。
这个题“远远达不到完全图,所以选用邻接表来作为图的存储比较合理”。
————————————————
版权声明:本文为CSDN博主「treble-z」的原创文章,遵循CC 4.0 BY-SA版权协议,转载请附上原文出处链接及本声明。
原文链接:https://blog.csdn.net/treblez/article/details/101017046
第一版(没写完DFS递归报错不知道怎么改,网上搜这题都用矩阵做的……)
#include
#include string.h>
#define MVNum 100
using namespace std;
int v1,v2,i,k,j,q;
typedef struct ArcNode
{
int adjvex;
struct ArcNode * nextarc;
}ArcNode;
typedef struct VNode
{
int Data;
ArcNode *firstarc;
}VNode,AdjList[MVNum];
typedef struct
{
AdjList vertices;
int vexnum,arcnum;
}ALGraph;
int LocateVex(ALGraph G,int u)
{
/* 初始条件: 图G存在bai,u和G中顶点有相同特征du*/
/* 操作结果: 若G中存在顶点u,则返回该顶点在图中位置;否则返回-1 */
int i;
for(i=0;ii)
if(u==G.vertices[i].Data)
return i;
return -1;
}
int CreateUDG(ALGraph &G) //构造一个无向链接表
{
ArcNode *p1,*p2;
cin>>G.vexnum>>G.arcnum>>q;
for(i=0;ii)
{
G.vertices[i].Data=i;
G.vertices[i].firstarc=NULL;
}
for(k=0;kk)
{
cin>>v1>>v2;
i=LocateVex(G,v1);
j=LocateVex(G,v2);
p1=new ArcNode;
p1->adjvex=j;
p1->nextarc=G.vertices[i].firstarc;
G.vertices[i].firstarc=p1;
p2=new ArcNode;
p2->adjvex=i;
p2->nextarc=G.vertices[j].firstarc;
G.vertices[j].firstarc=p2;
}
cout"Creatsuccessful"endl;
return 1;
}
int FirstAdjVex(ALGraph G,int u)
{
if(!G.vertices[u].firstarc) return -1;
return LocateVex(G, G.vertices[u].firstarc->adjvex);
}
int NextAdjVew(ALGraph G,int v,int w)
{
ArcNode *p=G.vertices[v].firstarc;
while(p&&LocateVex(G, p->adjvex)!=w)p=p->nextarc;
if(!p)return FirstAdjVex(G,v);
p=p->nextarc;
if(!p)return -1;
return LocateVex(G, p->adjvex);
}
bool visited[MVNum];
void DFS_AL(ALGraph G,int v)
{//图G为邻接表类型,从第V个顶点出发深度优先搜索遍历图G
ArcNode *p=new ArcNode;
int num=0;
num++;
if(num!=G.vexnum)
cout" ";
else
coutendl;
visited[v]=true; //访问第V个顶点,并置访问标志数组相应分量值为true
p=G.vertices[v].firstarc; //p指向v的边链表的第一个边结点
while(p!=NULL) //边结点非空
{
int w;
w=p->adjvex;//表示w是v的邻接点
if(!visited[w]) DFS_AL(G,w); //如果w未访问,则递归调用1条
p=p->nextarc;//p指向下一个边结点
}//while
}
int main( )
{
ALGraph G;
CreateUDG(G);
DFS_AL(G,q);
}

向ddl低头 遂使用邻接矩阵……
C++-PTA-6-7-1 地下迷宫探索
标签:存储结构 生活 战争 ++ 才智 UNC alt lis 方式
原文地址:https://www.cnblogs.com/loglian/p/13184188.html
评论


