Accelerate Framework in Swift

2021-05-08 04:29

阅读：1216

标签：The points 验证过问题线性 red 巩固等等 solution

介绍：

最近看到这篇文章有对Accelerate框架有一个介绍，自己也按照作者给的思路整理了一遍，也算是对这一框架的一个重新的回顾和学习，在以前研究AR先关只是的时候有接触到这个框架，赞具体里面的东西没有好好的实践一下，文章中有一些关于向量和矩阵运算的实际的Swift例子。可以简单的看一下。

Introduction to the Accelerate Framework in Swift

关于这个框架和文章其实在前面介绍iOS框架系列文章的时候有提过（第一篇），对这个框架有不清楚是做什么的可以翻翻我以前总结的文章。

由于下面的运算都是些向量和矩阵的运算，要是不清楚他们的概念和运算规则的可以看下面，先了解清楚再往下看，这些具体的内容在项目当中其实还是会用到的，比如说视频编码处理、AR等等。

向量

矩阵

Accelerate

使用之前请先导入这两个框架：

NOTE: 下面所有的例子全都是在 Playground 运行验证

import UIKit
import Accelerate
import simd

1、cblas_saxpy

函数cblas_saxpy(_:_:_:_:_:_:)是一个计算常数乘以一个向量加上一个向量的函数，具体的使用看下面的例子：

var x:[Float] = [1,2,3]
var y:[Float] = [4,5,6]

cblas_saxpy(3, 10, &x, 2, &y, 2)

具体的验证结果和详细的函数参数说明我们会在下面展示，大家可以先看上面给出的函数的说明推导一下结果：

技术图片

2、cblas_sdot 这个函数能帮助我们计算出两个向量的数量积： ∑ a[i] * b[i]

y = [4,5,6]
/// x*y = (1*4)+(2*5)+(3*6) = 32
/// 这个函数的具体的参数可以参考上面
cblas_sdot(3, &x, 1, &y, 1)

3、sgesv_ 这个函数可以帮我们解方程，比如下面的三元三次方程，具体的验证你可以自己尝试一下，了解一下函数的参数的意义，我们已经验证过就不再重复结果。

/// 下面我们解一个三元方程
/// 7x+5y-3z = 16
/// 3x-5y+2z = -8
/// 5x+3y-7z = 0
typealias LAInt = __CLPK_integer

var A:[Float] = [

    7, 3, 5,   /// x
    5, -5,3,   /// y
    -3,2,-7    /// z
]

var b:[Float] = [16,-8,0]

/// 定义要解的是一个几元方程
let equations = 3
/// 方程的个数
var numberOfEquations:LAInt = 3
var columnsIntA:LAInt = 3
var elementsIntB:LAInt = 3
/// 解的个数
var bSolutionCount:LAInt = 1
/// 验证是否计算有问题
var outputOk:LAInt = 0
/// [0,0,0]
var pivot = [LAInt](repeating: 0, count: equations)

/// 参数定义(按顺序):求解的线性方程个数、解的个数、系数矩阵A、
/// 矩阵A的列数、排列矩阵、系数向量B、向量B的列数、输出值。
sgesv_(&numberOfEquations, &bSolutionCount, &A, &columnsIntA, &pivot, &b, &elementsIntB, &outputOk)

/// outputOk == 0 说明一切计算正确
outputOk

/// 这个结果就是我们想要的答案 [1, 3, 2]
b

simd + vecLib + vDSP

具体的这三个框架的内容文章中有介绍过，我们这里主要的还是验证和实践一下里面的例子，看下面的代码。

1、矩阵的加法运算，看下面的例子，注意下面的不是向量的加法，留意区别不要混淆，代码简单我直接截图顺便看验证结果：

技术图片

2、vvfabsf 求绝对值的运算，代码如下：

/// fabs 求绝对值
func floats(_ n:Int32) -> [Float]{
    return [Float] (repeating: 0, count: Int(n))
}

var count:Int32 = 4
var aAbsoAbsolute = floats(count)

var c:[Float] = [-1,-2,-3,-4]
vvfabsf(&aAbsoAbsolute, &c, &count)

/// [1,2,3,4] 
aAbsoAbsolute

3、vvintf 小数取整求绝对值

c = [9.987,6.576,-3.345,-4.9]
var bAbsoAbsolute = floats(count)
vvintf(&bAbsoAbsolute, &c, &count)

/// [9, 6, -3, -4]
bAbsoAbsolute

4、sqrtf 开平方根

/// sqrt 开平方根  sqrtf()
c = [25,16,9,4]
var cAbsoAbsolute = floats(count)
vvsqrtf(&cAbsoAbsolute, &c, &count)

/// [5, 4, 3, 2]
cAbsoAbsolute

5、分数取逆这时候是分母和分子互换位置在做计算得来的

/// 分数取逆 这时候是分母和分子互换位置在做计算得来的
var d:[Float] = [1/3,1/5,3/9,4/2]
var dAbsoAbsolute = floats(count)
vvrecf(&dAbsoAbsolute, &d, &count)

/// [3, 5, 3, 0.5]
dAbsoAbsolute

6、vDSP_vdist 这个例子其实也很有趣的，具体的例子说明可以参考最上面文章的最后一个例子，我们直接看代码和验证的结果，代码里面有比较详细的说明，还是值得一看的，能帮助我们回忆巩固一些知识点：

var points:[CGPoint] = [
    
    CGPoint(x: 0, y: 0),
    CGPoint(x: 0, y: 10),
    CGPoint(x: 0, y: 20),
    CGPoint(x: 0, y: 30),
    CGPoint(x: 0, y: 40),
    CGPoint(x: 0, y: 50),
    CGPoint(x: 0, y: 60),
    CGPoint(x: 0, y: 70),
    CGPoint(x: 0, y: 80)
]
 
let path = UIBezierPath()
path.move(to: points[0])
 
// IMP: Remove the space between the  Float? in
    return Float(point.x)
}

var ys = points.compactMap { (point) -> Float? in
    return Float(point.y)
}

var distance:[Float] = [Float](repeating: 0, count: points.count)

vDSP_vdist(&xs, 1, &ys, 1, &distance,1,vDSP_Length(points.count))

/// 遍历
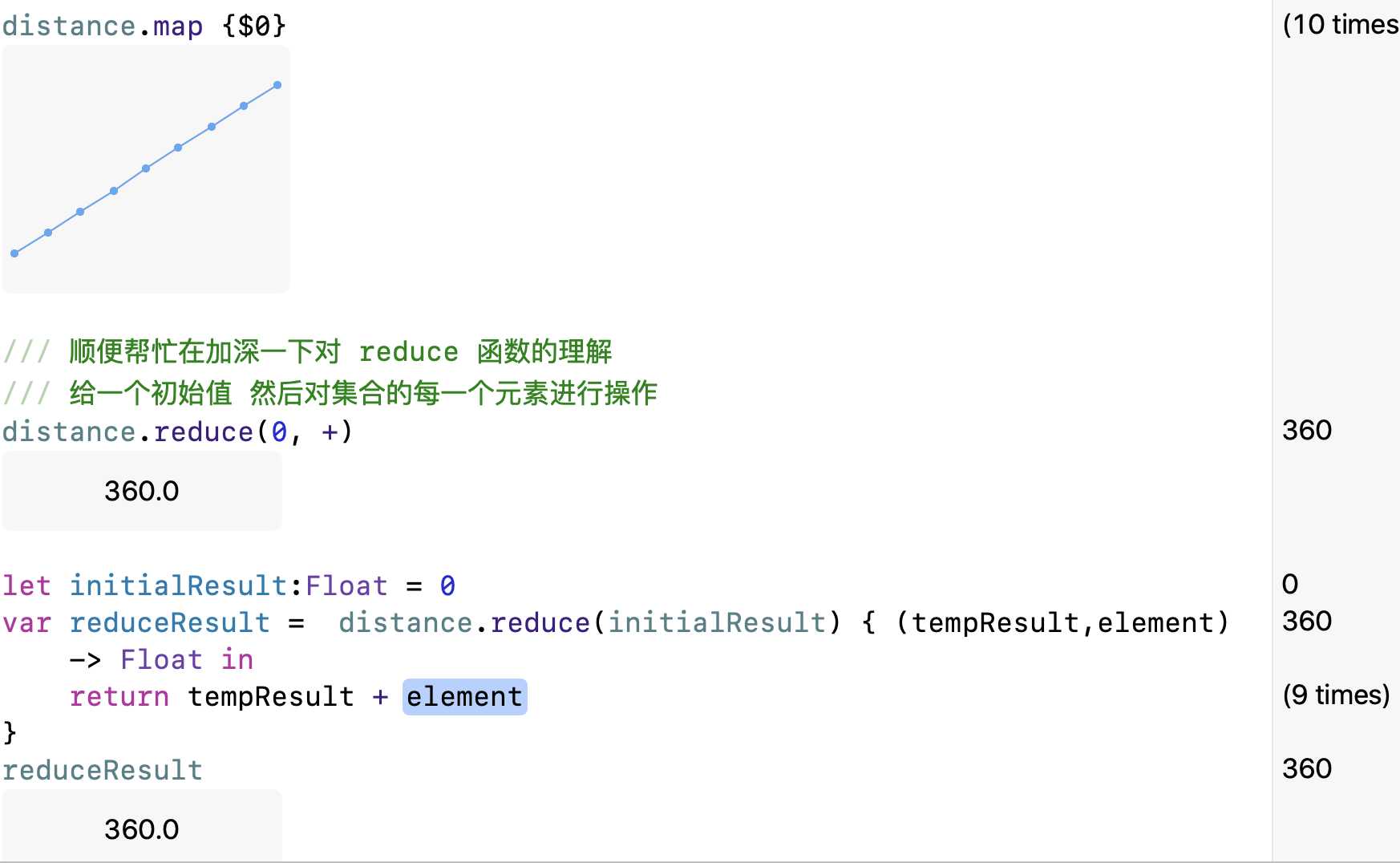
distance.map {$0}

/// 顺便帮忙在加深一下对 reduce 函数的理解
/// 给一个初始值 然后对集合的每一个元素进行操作
distance.reduce(0, +)

let initialResult:Float = 0
var reduceResult =  distance.reduce(initialResult) { (tempResult,element) -> Float in
    return tempResult + element
}

reduceResult

下面是上面例子的结果验证：技术图片