关于图的一些寻路算法(课题有用)
2021-05-13 06:29
标签:检测 get eth arraylist str 开启 寻路 def 显示 漫画:图的 “最短路径” 问题 1.当图为无权图时,可以用广度遍历算法bfs获得相隔层次最少的路径。 先加入一个顶点,再while循环,循环中先出一个,再判断是否出的该点是否访问过。若访问过,则continue。continue语句的作度用是跳过循环本中剩余的语句而强行执行下一次循环。 (一个疑问,这样遍历了所有的啊怎么找到路径呢? 2.换成带权图,最短路径就不一定是层次最少的了。 ------------------------------------------------------------------------------------------------- ps:(这个好:数据结构与算法——图最短路径 讲得很全但是没代码。。floyd代码还有错。) pps:(这个图的遍历也好:数据结构与算法:三十张图弄懂「图的两种遍历方式」 dfs用栈好像是做保存顶点用的,不用保存的话就不需要。) ---------------------------------------------------------------------------------------------------- 著名单源的最短路径算法。指定一个点(源点)到其余各个顶点的最短路径,也叫做“单源最短路径”。例如求下图中的1号顶点到2、3、4、5、6号顶点的最短路径。 算法的基本思想是:从源点出发,每次选择离源点最近的一个顶点前进,然后以该顶点为中心进行扩展,最终得到源点到其余所有点的最短路径。 需要一个记录其他节点的距离表,从最短邻节点开始每一个节点遍历刷新一次最短距离表。 代码还是看最顶上的漫画链接,但是转载不过来。然后本地保存也有dijkstra和floyd,但是没有注释真的看不懂。。。 Dijkstra算法算是贪心思想实现的,首先把起点到所有点的距离存下来找个最短的,然后松弛一次再找出最短的,所谓的松弛操作就是,遍历一遍看通过刚刚找到的距离最短的点作为中转站会不会更近(难怪接下来是看v3的出度有哪些,因为只有把v3当中转站的才有机会更新),如果更近了就更新距离(但此时更新的距离不一定之后就不会更新,还需要去比较的。之后不会更新的只有中转站的确定了),这样把所有的点找遍之后就存下了起点基于该点中转后到其他所有点的最短距离。 因为目前离 v1顶点最近的是 v3顶点,并且这个图所有的边都是正数,那么肯定不可能通过第三个顶点中转,使得 v1顶点到 v3顶点的路程进一步缩短了。因为 v1顶点到其它顶点的路程肯定没有 v1到 v3顶点短。由此确定了一个顶点的最短路径。接下来把v3当中转站看V3的出度。资料是这里 出度V4完了以后是重新开始找除中转站外最短点,再把最短点当中转站进行更新操作,以此类推下去。 代码:有注释,懂了。每次就是就是找最短中转点和更新。 Floyd算法是一个经典的动态规划算法。如下案例,可以为多源求最短路径。 其主要思想为:从任意顶点u到任意顶点v的最短路径不外乎2种可能,一是直接从u到v,二是从u经过若干个顶点k到v。所以,我们假设dist(u,v)为顶点u到顶点v的最短路径的距离,对于每一个顶点k,我们检查dist(u,k) + dist(k,v) ,如果成立,证明从u到k再到v的路径比u直接到v的路径短,我们便设置dist(u,v) = dist(u,k) + dist(k,v),这样一来,当我们遍历完所有顶点k,dist(u,v)中记录的便是u到v的最短路径的距离。(后面是分段吗?不是!!后面是取代!赋值!!!后面的赋完值就不管了!成为新的dist,别的遍历的点再去跟这个新的dist比!!我为什么会以为是分两段然后别的点再分四段。。这是什么危险的惯性思维。。。??) (1)从任意一条单边路径开始。所有两点之间的距离是边的权,如果两点之间没有边相连,则权为无穷大。 Floyd算法是一种暴力破解的方式获取最短路径。Floyd算法的时间复杂度为O(n^3),空间复杂度为O(n^2)。Floyd算法可以获得任意顶点对之间的最短路径。 ----------------------------------------------------------------------------------------------- dijkstra和floyd的区别就是前者只能处理单源非负,后者可以多源有负。前者基于贪心思想,后者基于动态规划。动态规划可解贪心,但贪心不可解动态规划。 参考 (但博主floyd那里k应该在最外层,写错了) 好像不再是图的顶点找顶点的问题了。:https://blog.csdn.net/qq_36946274/article/details/81982691 我们需要从 open list 中选一个与起点 A 相邻的方格,按下面描述的一样或多或少的重复前面的步骤。但是到底选择哪个方格好呢?具有最小 F 值的那个。 计算出组成路径的方格的关键是下面这个等式: F = G + H 这里, G = 从起点 A 移动到指定方格(应该就是第N步的意思)的移动代价,沿着到达该方格而生成的路径。既然我们是沿着到达指定方格的路径来计算 G 值,那么计算出该方格的 G 值的方法就是找出其父亲的 G 值,然后按父亲是直线方向还是斜线方向加上 10 (直线)或 1。 H = 从指定的方格移动到终点 B 的估算成本。这个通常被称为试探法,有点让人混淆。为什么这么叫呢,因为这是个猜测。直到我们找到了路径我们才会知道真正的距离,因为途中有各种各样的东西 ( 比如墙壁,水等 ) 。 有很多方法可以估算 H 值。这里我们使用 Manhattan 方法,计算从当前方格横向或纵向移动到达目标所经过的方格数,忽略对角移动,然后把总数乘以 10 。之所以叫做 Manhattan 方法,是因为这很像统计从一个地点到另一个地点所穿过的街区数,而你不能斜向穿过街区。重要的是,计算 H 时,要忽略路径中的障碍物。这是对剩余距离的估算值,而不是实际值,因此才称为试探法。 把 G 和 H 相加便得到 F 。我们第一步的结果如下图所示。每个方格都标上了 F , G , H 的值,就像起点右边的方格那样,左上角是 F ,左下角是 G ,右下角是 H 。 (也就是说 走第一步之前 A周围的8个点都要先算一遍走直线到终点不考虑障碍物的H值。错了错了,不是走,是open list范围) 右边这个F=G+H=40是最小的 后续看前面链接。。它这不是步子,是待处理方格。最终路径是从终点回溯。 那么我们怎么样去确定实际路径呢?很简单,从终点开始,按着箭头向父节点移动,这样你就被带回到了起点,这就是你的路径。 ------------------------------------------------------------------------------------------------------------------- 启发函数(Heuristics function) h值属于估算成本,不同的估算方法对应不同的结果。选取适合的估算方法需要根据实际场景而定。我们成这种估算函数为启发函数,例如,允许4个方向走,那么可以采用曼哈顿距离(Manhattan distance), 即横向和竖向走到终点的距离之和。启发函数的作用在于,当你把启发代价设定的比实际代价更大时,那么搜索速度会变得更快,但结果可能不是最优的路径。相反,启发代价比实际的小,那么搜索变慢,得到一个最优路径。这是速度与最优解之间的权衡 开放列表(Open List) 以上是A*的关键点,尤其是启发函数,如果没有启发函数,则A*就退化成了Dijkstra算法,是运行效率重要还是找到最佳路径重要,全靠启发函数来调节,因此也被归为启发式算法。 A*算法的具体步骤: 总结起来,就这么4步骤,非常简单。 本地的代码: 关于图的一些寻路算法(课题有用) 标签:检测 get eth arraylist str 开启 寻路 def 显示 原文地址:https://www.cnblogs.com/gezi1007/p/13097022.html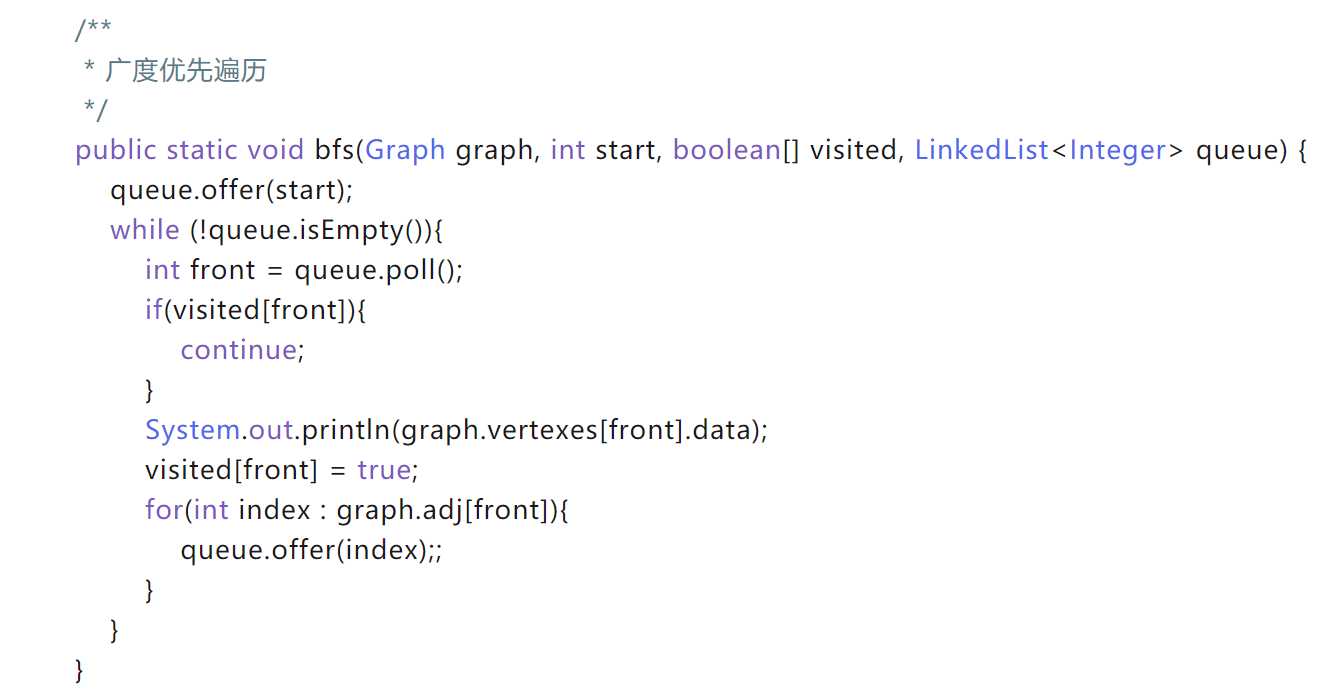
3.dijkstra算法
import java.util.Arrays;
public class DijkstraAlgorithm {
public static void main(String[] args) {
char[] vertex = { ‘A‘, ‘B‘, ‘C‘, ‘D‘, ‘E‘, ‘F‘, ‘G‘ };
// 邻接矩阵
int[][] matrix = new int[vertex.length][vertex.length];
final int N = 65535;// 表示不可以连接
matrix[0] = new int[] { N, 5, 7, N, N, N, 2 };
matrix[1] = new int[] { 5, N, N, 9, N, N, 3 };
matrix[2] = new int[] { 7, N, N, N, 8, N, N };
matrix[3] = new int[] { N, 9, N, N, N, 4, N };
matrix[4] = new int[] { N, N, 8, N, N, 5, 4 };
matrix[5] = new int[] { N, N, N, 4, 5, N, 6 };
matrix[6] = new int[] { 2, 3, N, N, 4, 6, N };
// 创建 Graph对象
Graph graph = new Graph(vertex, matrix);
// 测试, 看看图的邻接矩阵是否ok
graph.showGraph();
// 测试迪杰斯特拉算法
graph.dsj(2);// C为出发点
// 打印结果
graph.showDijkstra();
}
}
class Graph {
private char[] nodes; // 节点数组
private int[][] matrix; // 邻接矩阵
private NodesInfo nodesInfo; // 访问节点后的记录信息
// 构造器
public Graph(char[] vertex, int[][] matrix) {
this.nodes = vertex;
this.matrix = matrix;
}
// 输出结果
public void showDijkstra() {
nodesInfo.show();
}
// 输出图
public void showGraph() {
for (int[] link : matrix) {
System.out.println(Arrays.toString(link));
}
}
/**
* 迪杰斯特拉算法实现
*
* @param index 表示出发节点对应的下标
*/
public void dsj(int index) {
nodesInfo = new NodesInfo(nodes.length, index);
update(index);// 更新index节点到周围节点的距离、周围节点的前驱节点
// 访问其余的vertex.length-1个节点
for (int j = 1; j ) {
index = nodesInfo.findNextNode();// 找到一个[到已经访问过的所有节点的最近距离最小]的节点
update(index); // 更新index节点到周围节点的距离、周围节点的前驱节点
}
}
/**
* 更新index下标节点到周围节点的距离、周围节点的前驱节点
*
* @param index
*/
private void update(int index) {
int curLen = 0;
// 遍历邻接矩阵的 matrix[index] 行
for (int j = 0; j ) {
// len = 出发节点到index节点的距离 + 从index节点到j节点的距离
curLen = nodesInfo.getLenFromBegin(index) + matrix[index][j];
// j节点没有被访问过,并且距离出发点小于表中记录
if (!nodesInfo.hasVisited(j) && curLen nodesInfo.getLenFromBegin(j)) {
nodesInfo.setPreNode(j, index); // 更新j节点的前驱为index节点
nodesInfo.setLenFromBegin(j, curLen); // 更新出发节点到j节点的距离
}
}
}
}
// 已访问节点集合
class NodesInfo {
// 下标对应节点是否访问过: 1=访问过 0=未访问
public int[] visitedFlag;
// 下标对应节点的前驱
public int[] preNode;
// 记录出发节点到其他所有节点的距离
public int[] lenFromBegin;
/**
* 构造器
*
* @param length :表示节点的个数
* @param index: 出发节点。 比如G节点下标是6
*/
public NodesInfo(int length, int index) {
this.visitedFlag = new int[length];
this.preNode = new int[length];
this.lenFromBegin = new int[length];
// 初始化 dis数组
Arrays.fill(lenFromBegin, 65535);
this.visitedFlag[index] = 1; // 设置出发节点被访问过
this.lenFromBegin[index] = 0;// 设置出发节点的访问距离为0
}
/**
* 功能: 判断index节点是否被访问过
*
* @param index
* @return 如果访问过,就返回true, 否则访问false
*/
public boolean hasVisited(int index) {
return visitedFlag[index] == 1;
}
/**
* 功能: 更新出发节点到index节点的距离
*
* @param index
* @param len
*/
public void setLenFromBegin(int index, int len) {
lenFromBegin[index] = len;
}
/**
* 功能: 更新pre这个节点的前驱节点为index节点
*
* @param pre
* @param index
*/
public void setPreNode(int pre, int index) {
preNode[pre] = index;
}
/**
* 功能:返回出发节点到index节点的距离
*
* @param index
*/
public int getLenFromBegin(int index) {
return lenFromBegin[index];
}
/**
* 寻找一个新的距离最短的访问节点。这个节点的要求是:未访问过,并且从已访问节点到此点是最短路径。
*
* @return 新的访问节点
*/
public int findNextNode() {
int min = 65535, index = 0;
for (int i = 0; i // 从所有节点中寻找
if (visitedFlag[i] == 0 && lenFromBegin[i] // 未访问过,并且从已访问节点到此点是最短路径
min = lenFromBegin[i];
index = i;
}
}
// 更新 index 节点被访问过
visitedFlag[index] = 1;
return index;
}
// 显示最后的结果,即:输出三个数组
public void show() {
System.out.println("==========================");
// 输出already_arr
for (int i : visitedFlag) {
System.out.print(i + " ");
}
System.out.println();
// 输出pre_visited
for (int i : preNode) {
System.out.print(i + " ");
}
System.out.println();
// 输出dis
for (int i : lenFromBegin) {
System.out.print(i + " ");
}
System.out.println();
// 为了好看最后的最短距离,我们处理
char[] vertex = { ‘A‘, ‘B‘, ‘C‘, ‘D‘, ‘E‘, ‘F‘, ‘G‘ };
int count = 0;
for (int i : lenFromBegin) {
if (i != 65535) {
System.out.print(vertex[count] + "(" + i + ") ");
} else {
System.out.println("N ");
}
count++;
}
System.out.println();
}
}
4. 弗洛伊德(Floyd)算法
4.1 算法概述
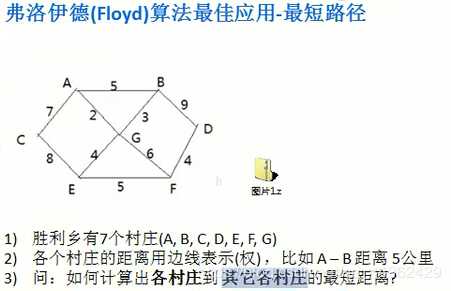
4.2 算法流程
(2)对于每一对顶点u和v,看看是否存在一个顶点w使得从u到w再到v比己知的路径更短。如果是更新它,存住。package com.self.tenAlgorithm;
import java.util.Arrays;
public class FloydAlgorithm {
final static int N = 65535;
public static void main(String[] args) {
char[] vertex = {‘A‘,‘B‘,‘C‘,‘D‘,‘E‘,‘F‘,‘G‘};
//创建邻接矩阵
int[][] matrix = new int[vertex.length][vertex.length];
matrix[0] = new int[]{0,5,7,N,N,N,2};
matrix[1] = new int[]{5,0,N,9,N,N,3};
matrix[2] = new int[]{7,N,0,N,8,N,N};
matrix[3] = new int[]{N,9,N,0,N,4,N};
matrix[4] = new int[]{N,N,8,N,0,5,4};
matrix[5] = new int[]{N,N,N,4,5,0,6};
matrix[6] = new int[]{2,3,N,N,4,6,0};
Graph0 graph = new Graph0(vertex, vertex.length,matrix);
graph.floyd();
graph.show();
}
}
//创建图
class Graph0{
private char[] vertex; //存放顶点属主
private int[][] dis; //保存,从各个顶点出发到其他顶点的距离,最后的结果,也是保留在该数组
private int[][] pre; //保存到达目标顶点的前驱节点
/**
* 功能: 构造器
* @param vertex 顶点数组
* @param length 大小
* @param matrix 领接矩阵
*/
public Graph0(char[] vertex, int length,int[][] matrix) {
this.vertex = vertex;
this.dis = matrix;
this.pre = new int[length][length];
//对pre数组初始化,注意存放的是前驱顶点的下标
for (int i = 0; i ) {
Arrays.fill(pre[i],i);
}
}
/**
* 功能:显示pre数组和dis数组
*/
public void show(){
char[] vertex = {‘A‘,‘B‘,‘C‘,‘D‘,‘E‘,‘F‘,‘G‘};
for (int k = 0; k ) {
//先将pre数组输出的一行
for (int i = 0; i ) {
System.out.print(vertex[pre[k][i]]+" ");
}
System.out.println();
for (int i = 0; i ) {
System.out.print("("+vertex[k]+"到"+vertex[i]+"的最短路径是"+dis[k][i]+") ");
}
System.out.println();
System.out.println();
}
}
/**
* 弗洛伊德算法实现
*/
public voidint len = 0; //变量保存距离
//对中间顶点遍历 k就是中间顶点的下标 最外层为插入!!!!
for (int k = 0; k ) {
//从i顶点开始出发
for (int i = 0; i ) {
//到达j顶点
for (int j = 0; j ) {
len = dis[i][k] + dis[k][j];
if(len dis[i][j]){
dis[i][j] = len; //更新距离
pre[i][j] = pre[k][j]; //更新前驱节点
}
}
}
}
}
}
5.A*算法
路径排序(Path Sorting)
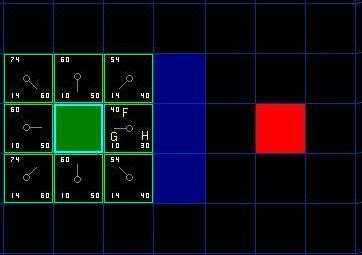
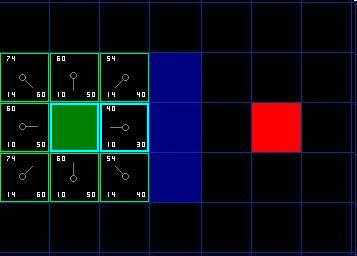
开放列表实际上是一个待检测的格子列表,对应的,我们把检测过的格子放入Close List中。
1. 把起点加入openlist
2. 遍历openlist,找到F值最小的节点,把它作为当前处理的节点,并把该节点加入closelist中
3. 对该节点的8个相邻格子进行判断,如果格子是不可抵达的或者在closelist中,则忽略它,否则如下操作:
a. 如果相邻格子不在openlist中,把它加入,并将parent设置为该节点和计算f,g,h值
b.如果相邻格子已在openlist中,并且新的G值比旧的G值小,则把相邻格子的parent设置为该节点,并且重新计算f值。
4. 重复2,3步,直到终点加入了openlist中,表示找到路径;或者openlist空了,表示没有路径。
————————————————
版权声明:本文为CSDN博主「booirror」的原创文章,遵循CC 4.0 BY-SA版权协议,转载请附上原文出处链接及本声明。
原文链接:https://blog.csdn.net/booirror/article/details/50834915import java.util.*;
//A*算法
public class AStar {
private int[][] map;// 地图(1可通过 0不可通过)
private List