标签:std fine 树节点 实现 完成 href 函数 out nim
AVL树的介绍
AVL树是高度平衡的而二叉树。它的特点是:AVL树中任何节点的两个子树的高度最大差别为1。
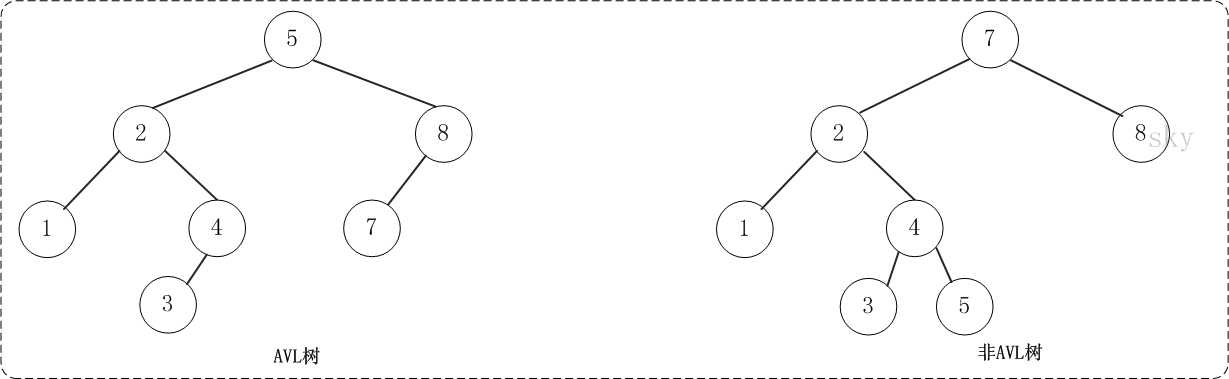
上面的两张图片,左边的是AVL树,它的任何节点的两个子树的高度差别都
AVL树的C++实现
1. 节点
1.1 AVL树节点
template
class AVLTreeNode{
public:
T key; // 关键字(键值)
int height; // 高度
AVLTreeNode *left; // 左孩子
AVLTreeNode *right; // 右孩子
AVLTreeNode(T value, AVLTreeNode *l, AVLTreeNode *r):
key(value), height(0),left(l),right(r) {}
};
AVLTreeNode是AVL树的节点类,它包括的几个组成对象:
(01) key -- 是关键字,是用来对AVL树的节点进行排序的。
(02) left -- 是左孩子。
(03) right -- 是右孩子。
(04) height -- 是高度。
1.2 AVL树
template
class AVLTree {
private:
AVLTreeNode *mRoot; // 根结点
public:
AVLTree();
~AVLTree();
// 获取树的高度
int height();
// 获取树的高度
int max(int a, int b);
// 前序遍历"AVL树"
void preOrder();
// 中序遍历"AVL树"
void inOrder();
// 后序遍历"AVL树"
void postOrder();
// (递归实现)查找"AVL树"中键值为key的节点
AVLTreeNode* search(T key);
// (非递归实现)查找"AVL树"中键值为key的节点
AVLTreeNode* iterativeSearch(T key);
// 查找最小结点:返回最小结点的键值。
T minimum();
// 查找最大结点:返回最大结点的键值。
T maximum();
// 将结点(key为节点键值)插入到AVL树中
void insert(T key);
// 删除结点(key为节点键值)
void remove(T key);
// 销毁AVL树
void destroy();
// 打印AVL树
void print();
private:
// 获取树的高度
int height(AVLTreeNode* tree) ;
// 前序遍历"AVL树"
void preOrder(AVLTreeNode* tree) const;
// 中序遍历"AVL树"
void inOrder(AVLTreeNode* tree) const;
// 后序遍历"AVL树"
void postOrder(AVLTreeNode* tree) const;
// (递归实现)查找"AVL树x"中键值为key的节点
AVLTreeNode* search(AVLTreeNode* x, T key) const;
// (非递归实现)查找"AVL树x"中键值为key的节点
AVLTreeNode* iterativeSearch(AVLTreeNode* x, T key) const;
// 查找最小结点:返回tree为根结点的AVL树的最小结点。
AVLTreeNode* minimum(AVLTreeNode* tree);
// 查找最大结点:返回tree为根结点的AVL树的最大结点。
AVLTreeNode* maximum(AVLTreeNode* tree);
// LL:左左对应的情况(左单旋转)。
AVLTreeNode* leftLeftRotation(AVLTreeNode* k2);
// RR:右右对应的情况(右单旋转)。
AVLTreeNode* rightRightRotation(AVLTreeNode* k1);
// LR:左右对应的情况(左双旋转)。
AVLTreeNode* leftRightRotation(AVLTreeNode* k3);
// RL:右左对应的情况(右双旋转)。
AVLTreeNode* rightLeftRotation(AVLTreeNode* k1);
// 将结点(z)插入到AVL树(tree)中
AVLTreeNode* insert(AVLTreeNode* &tree, T key);
// 删除AVL树(tree)中的结点(z),并返回被删除的结点
AVLTreeNode* remove(AVLTreeNode* &tree, AVLTreeNode* z);
// 销毁AVL树
void destroy(AVLTreeNode* &tree);
// 打印AVL树
void print(AVLTreeNode* tree, T key, int direction);
};
AVLTree是AVL树对应的类。它包含AVL树的根节点mRoot和AVL树的基本操作接口。需要说明的是:AVLTree中重载了许多函数。重载的目的是区分内部接口和外部接口,例如insert()函数而言,insert(tree, key)是内部接口,而insert(key)是外部接口。
1.2 树的高度
/*
* 获取树的高度
*/
template
int AVLTree::height(AVLTreeNode* tree)
{
if (tree != NULL)
return tree->height;
return 0;
}
template
int AVLTree::height()
{
return height(mRoot);
}
关于高度,有的地方将"空二叉树的高度是-1",而本文采用维基百科上的定义:树的高度为最大层次。即空的二叉树的高度是0,非空树的高度等于它的最大层次(根的层次为1,根的子节点为第2层,依次类推)。
1.3 比较大小
/*
* 比较两个值的大小
*/
template
int AVLTree::max(int a, int b)
{
return a>b ? a : b;
}
2. 旋转
如果在AVL树中进行插入或删除节点后,可能导致AVL树失去平衡。这种失去平衡的可以概括为4种姿态:LL(左左),LR(左右),RR(右右)和RL(右左)。下面给出它们的示意图:

上图中的4棵树都是"失去平衡的AVL树",从左往右的情况依次是:LL、LR、RL、RR。除了上面的情况之外,还有其它的失去平衡的AVL树,如下图:

上面的两张图都是为了便于理解,而列举的关于"失去平衡的AVL树"的例子。总的来说,AVL树失去平衡时的情况一定是LL、LR、RL、RR这4种之一,它们都由各自的定义:
(1) LL:LeftLeft,也称为"左左"。插入或删除一个节点后,根节点的左子树的左子树还有非空子节点,导致"根的左子树的高度"比"根的右子树的高度"大2,导致AVL树失去了平衡。
例如,在上面LL情况中,由于"根节点(8)的左子树(4)的左子树(2)还有非空子节点",而"根节点(8)的右子树(12)没有子节点";导致"根节点(8)的左子树(4)高度"比"根节点(8)的右子树(12)"高2。
(2) LR:LeftRight,也称为"左右"。插入或删除一个节点后,根节点的左子树的右子树还有非空子节点,导致"根的左子树的高度"比"根的右子树的高度"大2,导致AVL树失去了平衡。
例如,在上面LR情况中,由于"根节点(8)的左子树(4)的左子树(6)还有非空子节点",而"根节点(8)的右子树(12)没有子节点";导致"根节点(8)的左子树(4)高度"比"根节点(8)的右子树(12)"高2。
(3) RL:RightLeft,称为"右左"。插入或删除一个节点后,根节点的右子树的左子树还有非空子节点,导致"根的右子树的高度"比"根的左子树的高度"大2,导致AVL树失去了平衡。
例如,在上面RL情况中,由于"根节点(8)的右子树(12)的左子树(10)还有非空子节点",而"根节点(8)的左子树(4)没有子节点";导致"根节点(8)的右子树(12)高度"比"根节点(8)的左子树(4)"高2。
(4) RR:RightRight,称为"右右"。插入或删除一个节点后,根节点的右子树的右子树还有非空子节点,导致"根的右子树的高度"比"根的左子树的高度"大2,导致AVL树失去了平衡。
例如,在上面RR情况中,由于"根节点(8)的右子树(12)的右子树(14)还有非空子节点",而"根节点(8)的左子树(4)没有子节点";导致"根节点(8)的右子树(12)高度"比"根节点(8)的左子树(4)"高2。
前面说过,如果在AVL树中进行插入或删除节点后,可能导致AVL树失去平衡。AVL失去平衡之后,可以通过旋转使其恢复平衡,下面分别介绍"LL(左左),LR(左右),RR(右右)和RL(右左)"这4种情况对应的旋转方法。
2.1 LL的旋转
LL失去平衡的情况,可以通过一次旋转让AVL树恢复平衡。如下图:
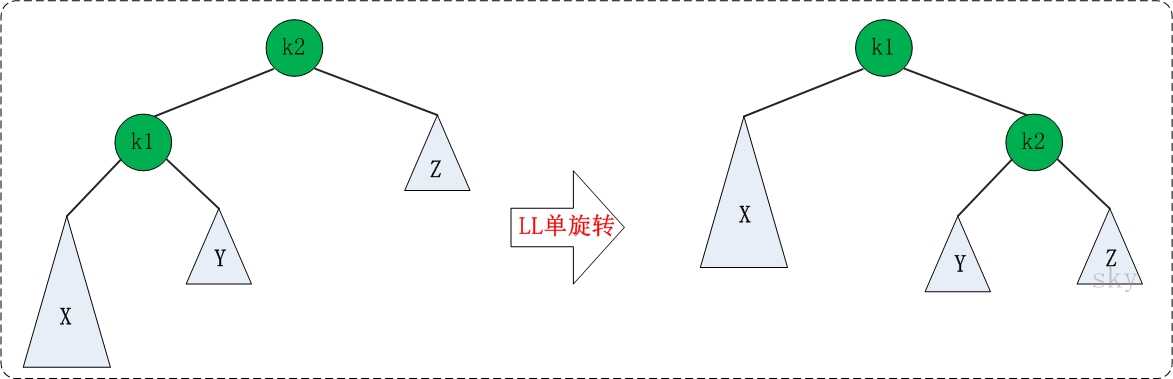
图中左边是旋转之前的树,右边是旋转之后的树。从中可以发现,旋转之后的树又变成了AVL树,而且该旋转只需要一次即可完成。
对于LL旋转,你可以这样理解为:LL旋转是围绕"失去平衡的AVL根节点"进行的,也就是节点k2;而且由于是LL情况,即左左情况,就用手抓着"左孩子,即k1"使劲摇。将k1变成根节点,k2变成k1的右子树,"k1的右子树"变成"k2的左子树"。
LL的旋转代码
/*
* LL:左左对应的情况(左单旋转)。
*
* 返回值:旋转后的根节点
*/
template
AVLTreeNode* AVLTree::leftLeftRotation(AVLTreeNode* k2)
{
AVLTreeNode* k1;
k1 = k2->left;
k2->left = k1->right;
k1->right = k2;
k2->height = max( height(k2->left), height(k2->right)) + 1;
k1->height = max( height(k1->left), k2->height) + 1;
return k1;
}
2.2 RR的旋转
理解了LL之后,RR就相当容易理解了。RR是与LL对称的情况!RR恢复平衡的旋转方法如下:
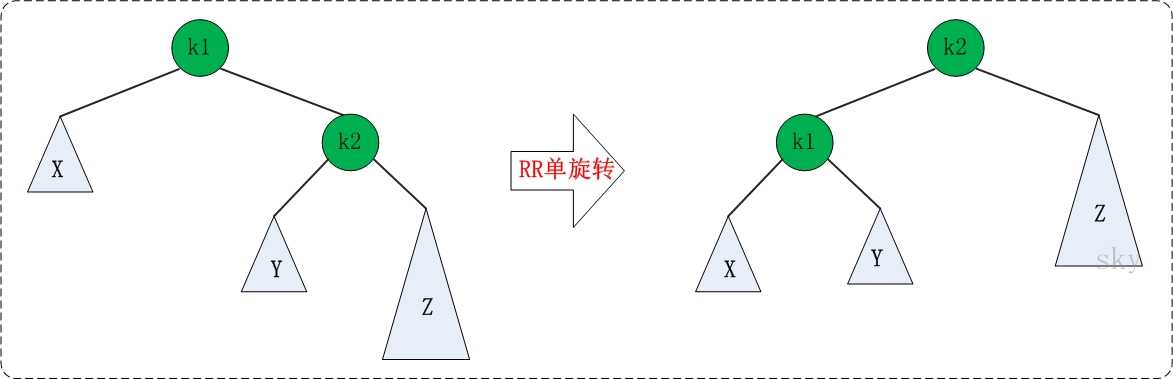
图中左边是旋转之前的树,右边是旋转之后的树。RR旋转也只需要一次即可完成。
RR的旋转代码
/*
* RR:右右对应的情况(右单旋转)。
*
* 返回值:旋转后的根节点
*/
template
AVLTreeNode* AVLTree::rightRightRotation(AVLTreeNode* k1)
{
AVLTreeNode* k2;
k2 = k1->right;
k1->right = k2->left;
k2->left = k1;
k1->height = max( height(k1->left), height(k1->right)) + 1;
k2->height = max( height(k2->right), k1->height) + 1;
return k2;
}
2.3 LR的旋转
LR失去平衡的情况,需要经过两次旋转才能让AVL树恢复平衡。如下图:

第一次旋转是围绕"k1"进行的"RR旋转",第二次是围绕"k3"进行的"LL旋转"。
LR的旋转代码
/*
* LR:左右对应的情况(左双旋转)。
*
* 返回值:旋转后的根节点
*/
template
AVLTreeNode* AVLTree::leftRightRotation(AVLTreeNode* k3)
{
k3->left = rightRightRotation(k3->left);
return leftLeftRotation(k3);
}
2.4 RL的旋转
RL是与LR的对称情况!RL恢复平衡的旋转方法如下:

第一次旋转是围绕"k3"进行的"LL旋转",第二次是围绕"k1"进行的"RR旋转"。
RL的旋转代码
/*
* RL:右左对应的情况(右双旋转)。
*
* 返回值:旋转后的根节点
*/
template
AVLTreeNode* AVLTree::rightLeftRotation(AVLTreeNode* k1)
{
k1->right = leftLeftRotation(k1->right);
return rightRightRotation(k1);
}
3. 插入
插入节点的代码
/*
* 将结点插入到AVL树中,并返回根节点
*
* 参数说明:
* tree AVL树的根结点
* key 插入的结点的键值
* 返回值:
* 根节点
*/
template
AVLTreeNode* AVLTree::insert(AVLTreeNode* &tree, T key)
{
if (tree == NULL)
{
// 新建节点
tree = new AVLTreeNode(key, NULL, NULL);
if (tree==NULL)
{
cout key) // 应该将key插入到"tree的左子树"的情况
{
tree->left = insert(tree->left, key);
// 插入节点后,若AVL树失去平衡,则进行相应的调节。
if (height(tree->left) - height(tree->right) == 2)
{
if (key left->key)
tree = leftLeftRotation(tree);
else
tree = leftRightRotation(tree);
}
}
else if (key > tree->key) // 应该将key插入到"tree的右子树"的情况
{
tree->right = insert(tree->right, key);
// 插入节点后,若AVL树失去平衡,则进行相应的调节。
if (height(tree->right) - height(tree->left) == 2)
{
if (key > tree->right->key)
tree = rightRightRotation(tree);
else
tree = rightLeftRotation(tree);
}
}
else //key == tree->key)
{
cout height = max( height(tree->left), height(tree->right)) + 1;
return tree;
}
template
void AVLTree::insert(T key)
{
insert(mRoot, key);
}
4. 删除
删除节点的代码
/*
* 删除结点(z),返回根节点
*
* 参数说明:
* tree AVL树的根结点
* z 待删除的结点
* 返回值:
* 根节点
*/
template
AVLTreeNode* AVLTree::remove(AVLTreeNode* &tree, AVLTreeNode* z)
{
// 根为空 或者 没有要删除的节点,直接返回NULL。
if (tree==NULL || z==NULL)
return NULL;
if (z->key key) // 待删除的节点在"tree的左子树"中
{
tree->left = remove(tree->left, z);
// 删除节点后,若AVL树失去平衡,则进行相应的调节。
if (height(tree->right) - height(tree->left) == 2)
{
AVLTreeNode *r = tree->right;
if (height(r->left) > height(r->right))
tree = rightLeftRotation(tree);
else
tree = rightRightRotation(tree);
}
}
else if (z->key > tree->key)// 待删除的节点在"tree的右子树"中
{
tree->right = remove(tree->right, z);
// 删除节点后,若AVL树失去平衡,则进行相应的调节。
if (height(tree->left) - height(tree->right) == 2)
{
AVLTreeNode *l = tree->left;
if (height(l->right) > height(l->left))
tree = leftRightRotation(tree);
else
tree = leftLeftRotation(tree);
}
}
else // tree是对应要删除的节点。
{
// tree的左右孩子都非空
if ((tree->left!=NULL) && (tree->right!=NULL))
{
if (height(tree->left) > height(tree->right))
{
// 如果tree的左子树比右子树高;
// 则(01)找出tree的左子树中的最大节点
// (02)将该最大节点的值赋值给tree。
// (03)删除该最大节点。
// 这类似于用"tree的左子树中最大节点"做"tree"的替身;
// 采用这种方式的好处是:删除"tree的左子树中最大节点"之后,AVL树仍然是平衡的。
AVLTreeNode* max = maximum(tree->left);
tree->key = max->key;
tree->left = remove(tree->left, max);
}
else
{
// 如果tree的左子树不比右子树高(即它们相等,或右子树比左子树高1)
// 则(01)找出tree的右子树中的最小节点
// (02)将该最小节点的值赋值给tree。
// (03)删除该最小节点。
// 这类似于用"tree的右子树中最小节点"做"tree"的替身;
// 采用这种方式的好处是:删除"tree的右子树中最小节点"之后,AVL树仍然是平衡的。
AVLTreeNode* min = maximum(tree->right);
tree->key = min->key;
tree->right = remove(tree->right, min);
}
}
else
{
AVLTreeNode* tmp = tree;
tree = (tree->left!=NULL) ? tree->left : tree->right;
delete tmp;
}
}
return tree;
}
template
void AVLTree::remove(T key)
{
AVLTreeNode* z;
if ((z = search(mRoot, key)) != NULL)
mRoot = remove(mRoot, z);
}
注意:关于AVL树的"前序遍历"、"中序遍历"、"后序遍历"、"最大值"、"最小值"、"查找"、"打印"、"销毁"等接口与"二叉查找树"基本一样,这些操作在"二叉查找树"中已经介绍过了,这里就不再单独介绍了。当然,后文给出的AVL树的完整源码中,有给出这些API的实现代码。这些接口很简单,Please RTFSC(Read The Fucking Source Code)!
完整的实现代码
AVL树的实现文件(AVRTree.h)
#ifndef _AVL_TREE_HPP_
#define _AVL_TREE_HPP_
#include
#include
using namespace std;
template
class AVLTreeNode{
public:
T key; // 关键字(键值)
int height; // 高度
AVLTreeNode *left; // 左孩子
AVLTreeNode *right; // 右孩子
AVLTreeNode(T value, AVLTreeNode *l, AVLTreeNode *r):
key(value), height(0),left(l),right(r) {}
};
template
class AVLTree {
private:
AVLTreeNode *mRoot; // 根结点
public:
AVLTree();
~AVLTree();
// 获取树的高度
int height();
// 获取树的高度
int max(int a, int b);
// 前序遍历"AVL树"
void preOrder();
// 中序遍历"AVL树"
void inOrder();
// 后序遍历"AVL树"
void postOrder();
// (递归实现)查找"AVL树"中键值为key的节点
AVLTreeNode* search(T key);
// (非递归实现)查找"AVL树"中键值为key的节点
AVLTreeNode* iterativeSearch(T key);
// 查找最小结点:返回最小结点的键值。
T minimum();
// 查找最大结点:返回最大结点的键值。
T maximum();
// 将结点(key为节点键值)插入到AVL树中
void insert(T key);
// 删除结点(key为节点键值)
void remove(T key);
// 销毁AVL树
void destroy();
// 打印AVL树
void print();
private:
// 获取树的高度
int height(AVLTreeNode* tree) ;
// 前序遍历"AVL树"
void preOrder(AVLTreeNode* tree) const;
// 中序遍历"AVL树"
void inOrder(AVLTreeNode* tree) const;
// 后序遍历"AVL树"
void postOrder(AVLTreeNode* tree) const;
// (递归实现)查找"AVL树x"中键值为key的节点
AVLTreeNode* search(AVLTreeNode* x, T key) const;
// (非递归实现)查找"AVL树x"中键值为key的节点
AVLTreeNode* iterativeSearch(AVLTreeNode* x, T key) const;
// 查找最小结点:返回tree为根结点的AVL树的最小结点。
AVLTreeNode* minimum(AVLTreeNode* tree);
// 查找最大结点:返回tree为根结点的AVL树的最大结点。
AVLTreeNode* maximum(AVLTreeNode* tree);
// LL:左左对应的情况(左单旋转)。
AVLTreeNode* leftLeftRotation(AVLTreeNode* k2);
// RR:右右对应的情况(右单旋转)。
AVLTreeNode* rightRightRotation(AVLTreeNode* k1);
// LR:左右对应的情况(左双旋转)。
AVLTreeNode* leftRightRotation(AVLTreeNode* k3);
// RL:右左对应的情况(右双旋转)。
AVLTreeNode* rightLeftRotation(AVLTreeNode* k1);
// 将结点(z)插入到AVL树(tree)中
AVLTreeNode* insert(AVLTreeNode* &tree, T key);
// 删除AVL树(tree)中的结点(z),并返回被删除的结点
AVLTreeNode* remove(AVLTreeNode* &tree, AVLTreeNode* z);
// 销毁AVL树
void destroy(AVLTreeNode* &tree);
// 打印AVL树
void print(AVLTreeNode* tree, T key, int direction);
};
/*
* 构造函数
*/
template
AVLTree::AVLTree():mRoot(NULL)
{
}
/*
* 析构函数
*/
template
AVLTree::~AVLTree()
{
destroy(mRoot);
}
/*
* 获取树的高度
*/
template
int AVLTree::height(AVLTreeNode* tree)
{
if (tree != NULL)
return tree->height;
return 0;
}
template
int AVLTree::height()
{
return height(mRoot);
}
/*
* 比较两个值的大小
*/
template
int AVLTree::max(int a, int b)
{
return a>b ? a : b;
}
/*
* 前序遍历"AVL树"
*/
template
void AVLTree::preOrder(AVLTreeNode* tree) const
{
if(tree != NULL)
{
coutkey left);
preOrder(tree->right);
}
}
template
void AVLTree::preOrder()
{
preOrder(mRoot);
}
/*
* 中序遍历"AVL树"
*/
template
void AVLTree::inOrder(AVLTreeNode* tree) const
{
if(tree != NULL)
{
inOrder(tree->left);
coutkey right);
}
}
template
void AVLTree::inOrder()
{
inOrder(mRoot);
}
/*
* 后序遍历"AVL树"
*/
template
void AVLTree::postOrder(AVLTreeNode* tree) const
{
if(tree != NULL)
{
postOrder(tree->left);
postOrder(tree->right);
coutkey
void AVLTree::postOrder()
{
postOrder(mRoot);
}
/*
* (递归实现)查找"AVL树x"中键值为key的节点
*/
template
AVLTreeNode* AVLTree::search(AVLTreeNode* x, T key) const
{
if (x==NULL || x->key==key)
return x;
if (key key)
return search(x->left, key);
else
return search(x->right, key);
}
template
AVLTreeNode* AVLTree::search(T key)
{
return search(mRoot, key);
}
/*
* (非递归实现)查找"AVL树x"中键值为key的节点
*/
template
AVLTreeNode* AVLTree::iterativeSearch(AVLTreeNode* x, T key) const
{
while ((x!=NULL) && (x->key!=key))
{
if (key key)
x = x->left;
else
x = x->right;
}
return x;
}
template
AVLTreeNode* AVLTree::iterativeSearch(T key)
{
return iterativeSearch(mRoot, key);
}
/*
* 查找最小结点:返回tree为根结点的AVL树的最小结点。
*/
template
AVLTreeNode* AVLTree::minimum(AVLTreeNode* tree)
{
if (tree == NULL)
return NULL;
while(tree->left != NULL)
tree = tree->left;
return tree;
}
template
T AVLTree::minimum()
{
AVLTreeNode *p = minimum(mRoot);
if (p != NULL)
return p->key;
return (T)NULL;
}
/*
* 查找最大结点:返回tree为根结点的AVL树的最大结点。
*/
template
AVLTreeNode* AVLTree::maximum(AVLTreeNode* tree)
{
if (tree == NULL)
return NULL;
while(tree->right != NULL)
tree = tree->right;
return tree;
}
template
T AVLTree::maximum()
{
AVLTreeNode *p = maximum(mRoot);
if (p != NULL)
return p->key;
return (T)NULL;
}
/*
* LL:左左对应的情况(左单旋转)。
*
* 返回值:旋转后的根节点
*/
template
AVLTreeNode* AVLTree::leftLeftRotation(AVLTreeNode* k2)
{
AVLTreeNode* k1;
k1 = k2->left;
k2->left = k1->right;
k1->right = k2;
k2->height = max( height(k2->left), height(k2->right)) + 1;
k1->height = max( height(k1->left), k2->height) + 1;
return k1;
}
/*
* RR:右右对应的情况(右单旋转)。
*
* 返回值:旋转后的根节点
*/
template
AVLTreeNode* AVLTree::rightRightRotation(AVLTreeNode* k1)
{
AVLTreeNode* k2;
k2 = k1->right;
k1->right = k2->left;
k2->left = k1;
k1->height = max( height(k1->left), height(k1->right)) + 1;
k2->height = max( height(k2->right), k1->height) + 1;
return k2;
}
/*
* LR:左右对应的情况(左双旋转)。
*
* 返回值:旋转后的根节点
*/
template
AVLTreeNode* AVLTree::leftRightRotation(AVLTreeNode* k3)
{
k3->left = rightRightRotation(k3->left);
return leftLeftRotation(k3);
}
/*
* RL:右左对应的情况(右双旋转)。
*
* 返回值:旋转后的根节点
*/
template
AVLTreeNode* AVLTree::rightLeftRotation(AVLTreeNode* k1)
{
k1->right = leftLeftRotation(k1->right);
return rightRightRotation(k1);
}
/*
* 将结点插入到AVL树中,并返回根节点
*
* 参数说明:
* tree AVL树的根结点
* key 插入的结点的键值
* 返回值:
* 根节点
*/
template
AVLTreeNode* AVLTree::insert(AVLTreeNode* &tree, T key)
{
if (tree == NULL)
{
// 新建节点
tree = new AVLTreeNode(key, NULL, NULL);
if (tree==NULL)
{
cout key) // 应该将key插入到"tree的左子树"的情况
{
tree->left = insert(tree->left, key);
// 插入节点后,若AVL树失去平衡,则进行相应的调节。
if (height(tree->left) - height(tree->right) == 2)
{
if (key left->key)
tree = leftLeftRotation(tree);
else
tree = leftRightRotation(tree);
}
}
else if (key > tree->key) // 应该将key插入到"tree的右子树"的情况
{
tree->right = insert(tree->right, key);
// 插入节点后,若AVL树失去平衡,则进行相应的调节。
if (height(tree->right) - height(tree->left) == 2)
{
if (key > tree->right->key)
tree = rightRightRotation(tree);
else
tree = rightLeftRotation(tree);
}
}
else //key == tree->key)
{
cout height = max( height(tree->left), height(tree->right)) + 1;
return tree;
}
template
void AVLTree::insert(T key)
{
insert(mRoot, key);
}
/*
* 删除结点(z),返回根节点
*
* 参数说明:
* tree AVL树的根结点
* z 待删除的结点
* 返回值:
* 根节点
*/
template
AVLTreeNode* AVLTree::remove(AVLTreeNode* &tree, AVLTreeNode* z)
{
// 根为空 或者 没有要删除的节点,直接返回NULL。
if (tree==NULL || z==NULL)
return NULL;
if (z->key key) // 待删除的节点在"tree的左子树"中
{
tree->left = remove(tree->left, z);
// 删除节点后,若AVL树失去平衡,则进行相应的调节。
if (height(tree->right) - height(tree->left) == 2)
{
AVLTreeNode *r = tree->right;
if (height(r->left) > height(r->right))
tree = rightLeftRotation(tree);
else
tree = rightRightRotation(tree);
}
}
else if (z->key > tree->key)// 待删除的节点在"tree的右子树"中
{
tree->right = remove(tree->right, z);
// 删除节点后,若AVL树失去平衡,则进行相应的调节。
if (height(tree->left) - height(tree->right) == 2)
{
AVLTreeNode *l = tree->left;
if (height(l->right) > height(l->left))
tree = leftRightRotation(tree);
else
tree = leftLeftRotation(tree);
}
}
else // tree是对应要删除的节点。
{
// tree的左右孩子都非空
if ((tree->left!=NULL) && (tree->right!=NULL))
{
if (height(tree->left) > height(tree->right))
{
// 如果tree的左子树比右子树高;
// 则(01)找出tree的左子树中的最大节点
// (02)将该最大节点的值赋值给tree。
// (03)删除该最大节点。
// 这类似于用"tree的左子树中最大节点"做"tree"的替身;
// 采用这种方式的好处是:删除"tree的左子树中最大节点"之后,AVL树仍然是平衡的。
AVLTreeNode* max = maximum(tree->left);
tree->key = max->key;
tree->left = remove(tree->left, max);
}
else
{
// 如果tree的左子树不比右子树高(即它们相等,或右子树比左子树高1)
// 则(01)找出tree的右子树中的最小节点
// (02)将该最小节点的值赋值给tree。
// (03)删除该最小节点。
// 这类似于用"tree的右子树中最小节点"做"tree"的替身;
// 采用这种方式的好处是:删除"tree的右子树中最小节点"之后,AVL树仍然是平衡的。
AVLTreeNode* min = maximum(tree->right);
tree->key = min->key;
tree->right = remove(tree->right, min);
}
}
else
{
AVLTreeNode* tmp = tree;
tree = (tree->left!=NULL) ? tree->left : tree->right;
delete tmp;
}
}
return tree;
}
template
void AVLTree::remove(T key)
{
AVLTreeNode* z;
if ((z = search(mRoot, key)) != NULL)
mRoot = remove(mRoot, z);
}
/*
* 销毁AVL树
*/
template
void AVLTree::destroy(AVLTreeNode* &tree)
{
if (tree==NULL)
return ;
if (tree->left != NULL)
destroy(tree->left);
if (tree->right != NULL)
destroy(tree->right);
delete tree;
}
template
void AVLTree::destroy()
{
destroy(mRoot);
}
/*
* 打印"二叉查找树"
*
* key -- 节点的键值
* direction -- 0,表示该节点是根节点;
* -1,表示该节点是它的父结点的左孩子;
* 1,表示该节点是它的父结点的右孩子。
*/
template
void AVLTree::print(AVLTreeNode* tree, T key, int direction)
{
if(tree != NULL)
{
if(direction==0) // tree是根节点
cout key key left, tree->key, -1);
print(tree->right,tree->key, 1);
}
}
template
void AVLTree::print()
{
if (mRoot != NULL)
print(mRoot, mRoot->key, 0);
}
#endif
AVL树的测试程序(AVLTreeTest.cpp)
/**
* C 语言: AVL树
*
* @author skywang
* @date 2013/11/07
*/
#include
#include "AVLTree.h"
using namespace std;
static int arr[]= {3,2,1,4,5,6,7,16,15,14,13,12,11,10,8,9};
#define TBL_SIZE(a) ( (sizeof(a)) / (sizeof(a[0])) )
int main()
{
int i,ilen;
AVLTree* tree=new AVLTree();
cout insert(arr[i]);
}
cout preOrder();
cout inOrder();
cout postOrder();
cout height() minimum() maximum() print();
i = 8;
cout remove(i);
cout height() ;
cout inOrder();
cout print();
// 销毁二叉树
tree->destroy();
return 0;
}
AVL树的C++测试程序
AVL树的测试程序代码(AVLTreeTest.cpp)在前面已经给出。在测试程序中,首先新建一棵AVL树,然后依次添加"3,2,1,4,5,6,7,16,15,14,13,12,11,10,8,9" 到AVL树中;添加完毕之后,再将8从AVL树中删除。AVL树的添加和删除过程如下图:
(01) 添加3,2
添加3,2都不会破坏AVL树的平衡性。
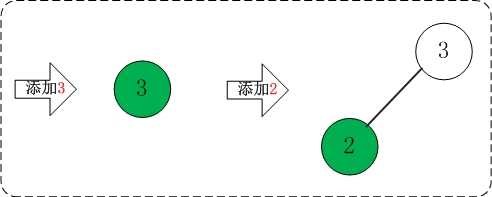
(02) 添加1
添加1之后,AVL树失去平衡(LL),此时需要对AVL树进行旋转(LL旋转)。旋转过程如下:
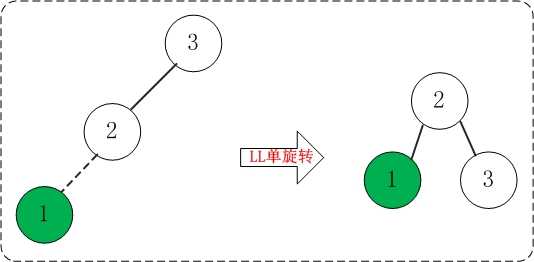
(03) 添加4
添加4不会破坏AVL树的平衡性。
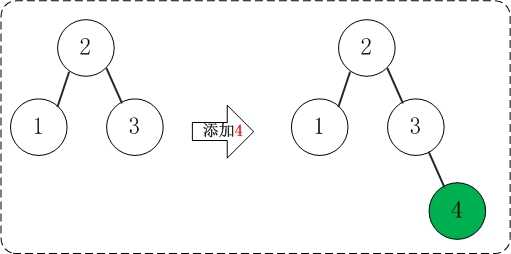
(04) 添加5
添加5之后,AVL树失去平衡(RR),此时需要对AVL树进行旋转(RR旋转)。旋转过程如下:
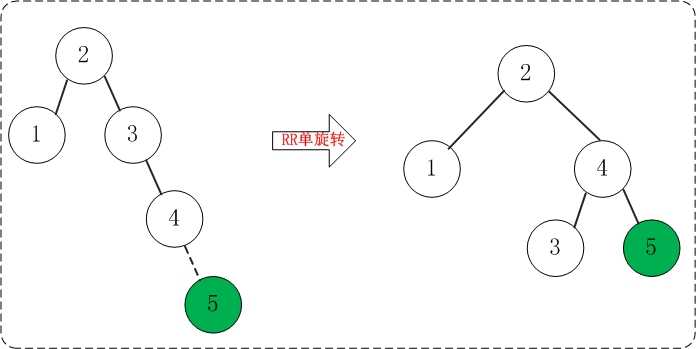
(05) 添加6
添加6之后,AVL树失去平衡(RR),此时需要对AVL树进行旋转(RR旋转)。旋转过程如下:
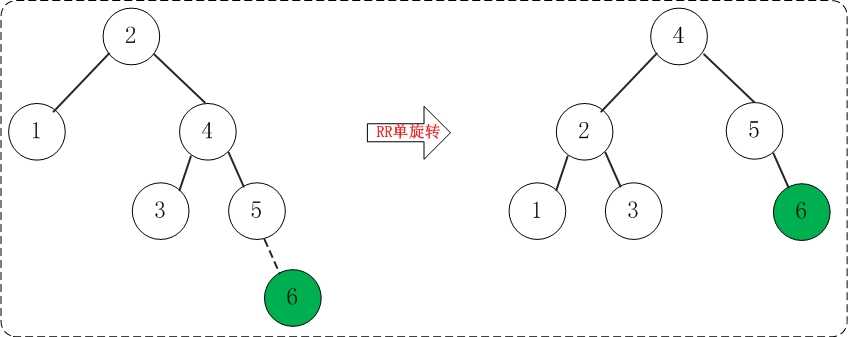
(06) 添加7
添加7之后,AVL树失去平衡(RR),此时需要对AVL树进行旋转(RR旋转)。旋转过程如下:
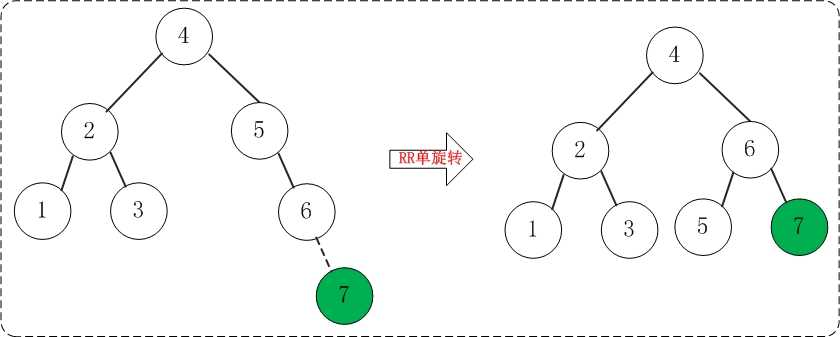
(07) 添加16
添加16不会破坏AVL树的平衡性。
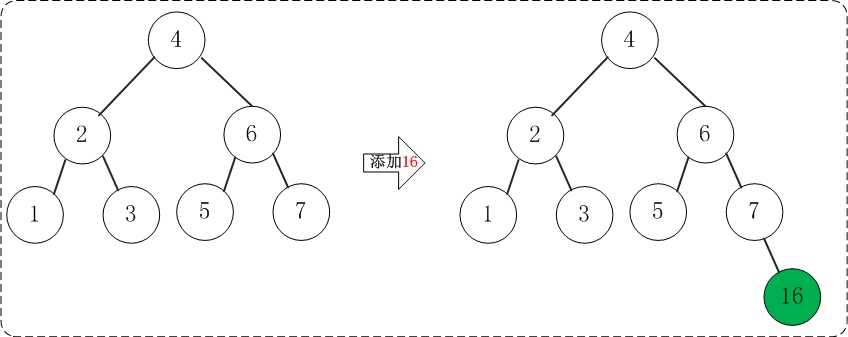
(08) 添加15
添加15之后,AVL树失去平衡(RR),此时需要对AVL树进行旋转(RR旋转)。旋转过程如下:
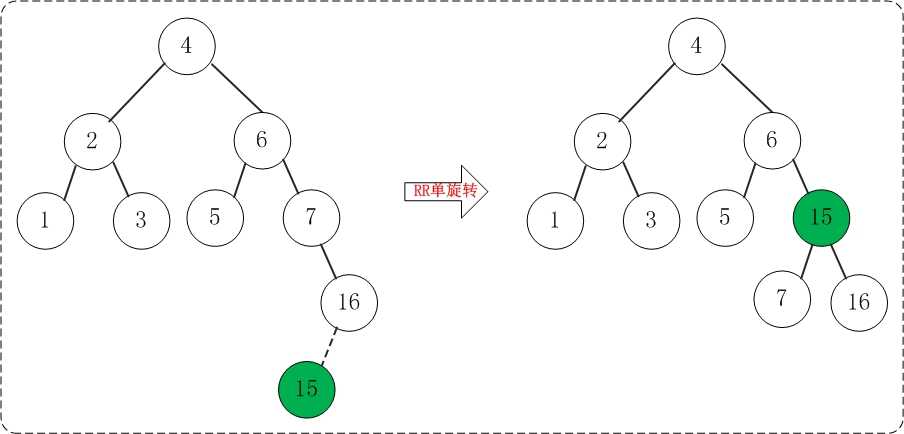
(09) 添加14
添加14之后,AVL树失去平衡(RL),此时需要对AVL树进行旋转(RL旋转)。旋转过程如下:
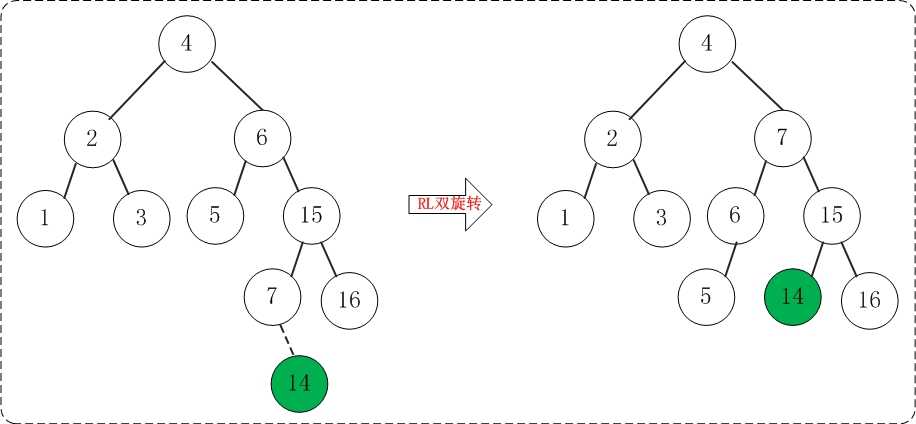
(10) 添加13
添加13之后,AVL树失去平衡(RR),此时需要对AVL树进行旋转(RR旋转)。旋转过程如下:
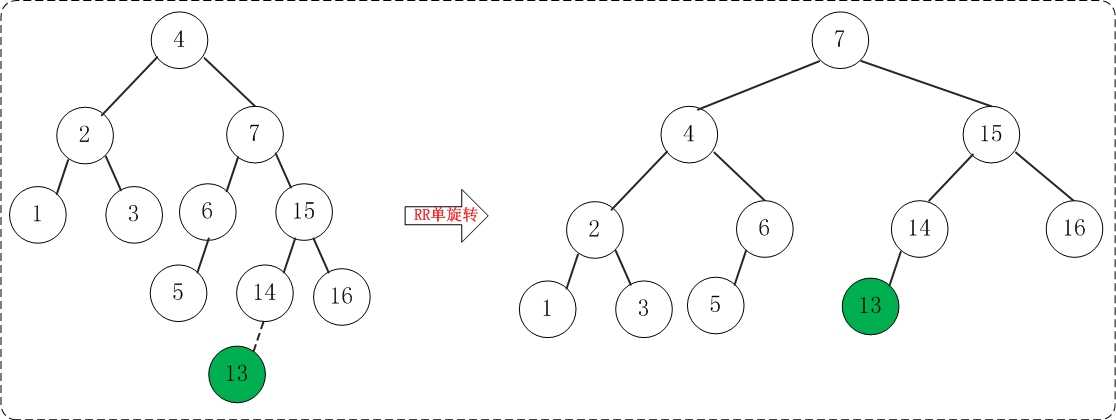
(11) 添加12
添加12之后,AVL树失去平衡(LL),此时需要对AVL树进行旋转(LL旋转)。旋转过程如下:
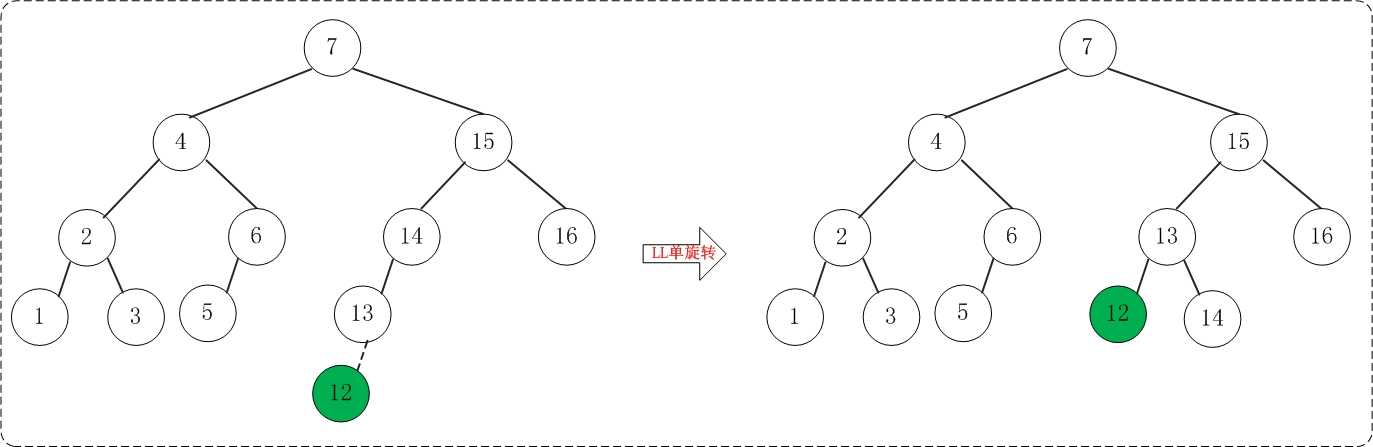
(12) 添加11
添加11之后,AVL树失去平衡(LL),此时需要对AVL树进行旋转(LL旋转)。旋转过程如下:
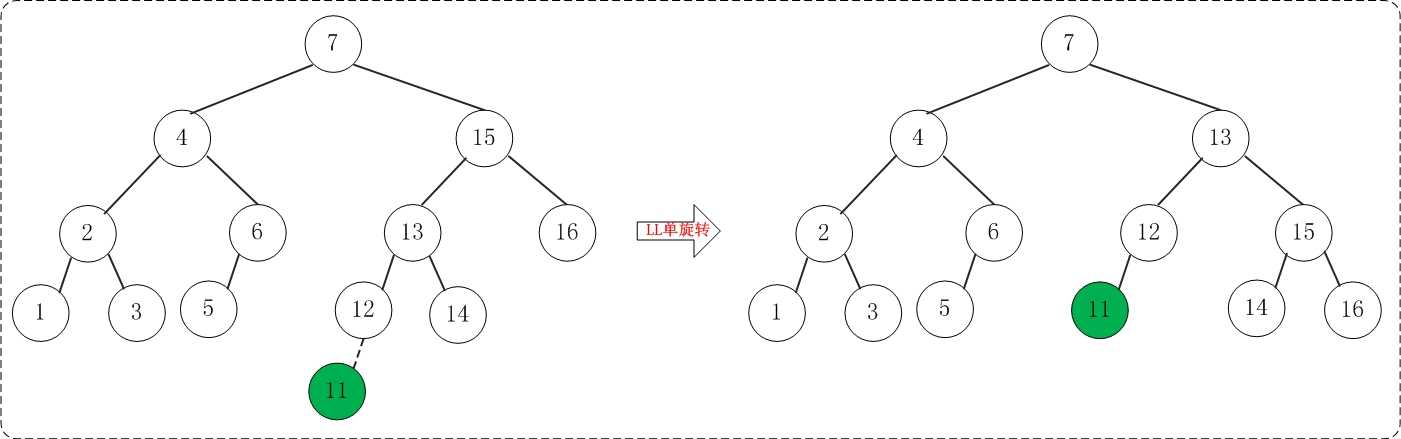
(13) 添加10
添加10之后,AVL树失去平衡(LL),此时需要对AVL树进行旋转(LL旋转)。旋转过程如下:
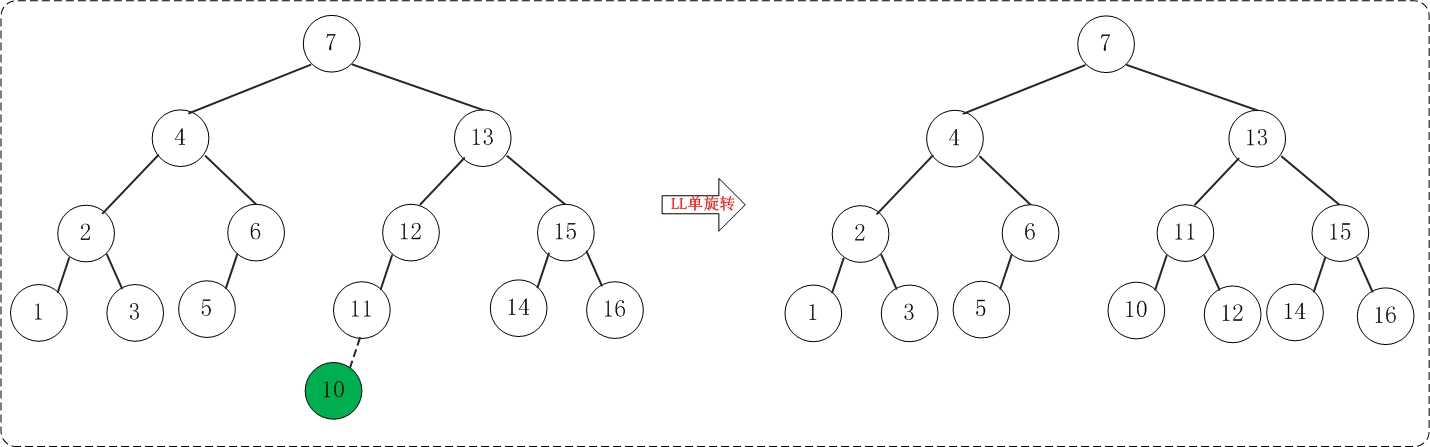
(14) 添加8
添加8不会破坏AVL树的平衡性。
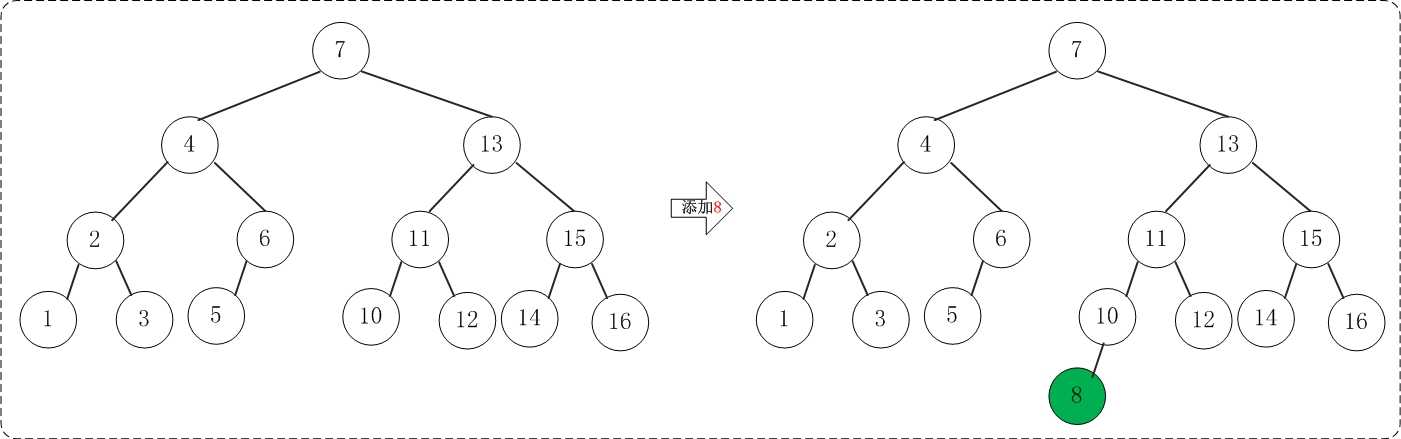
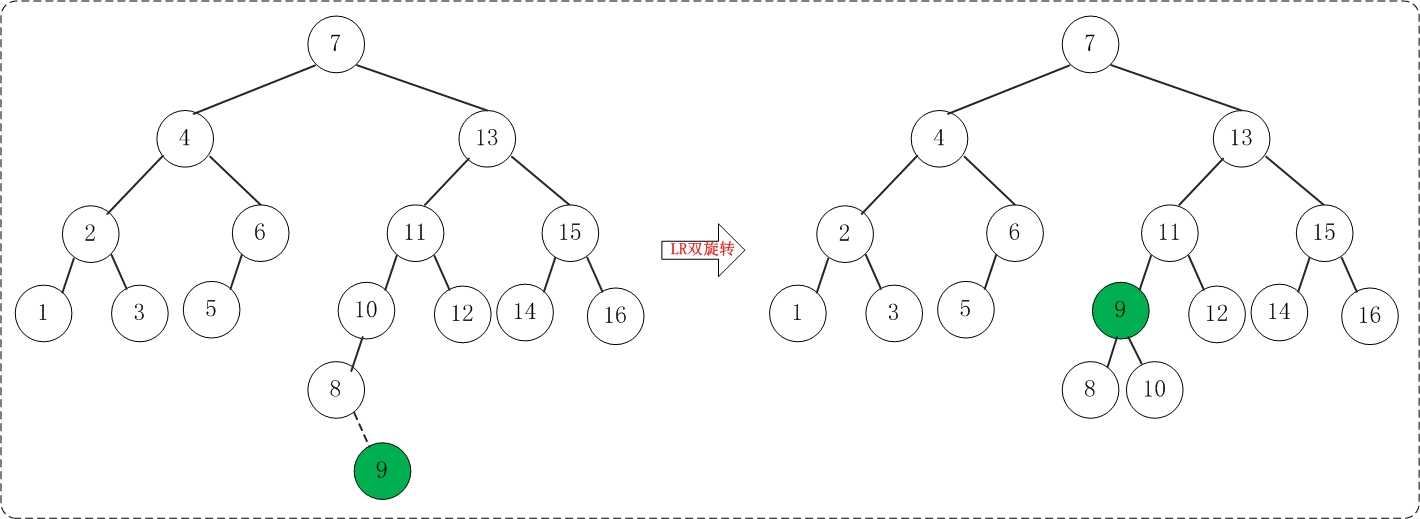
(15) 添加9
但是添加9之后,AVL树失去平衡(LR),此时需要对AVL树进行旋转(LR旋转)。旋转过程如下:
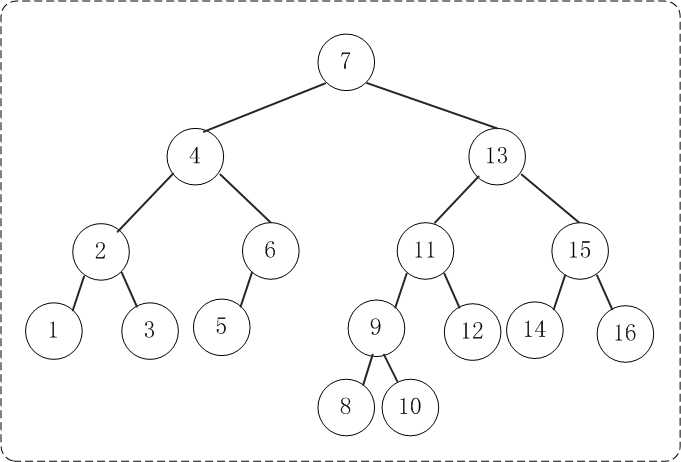
添加完所有数据之后,得到的AVL树如下:
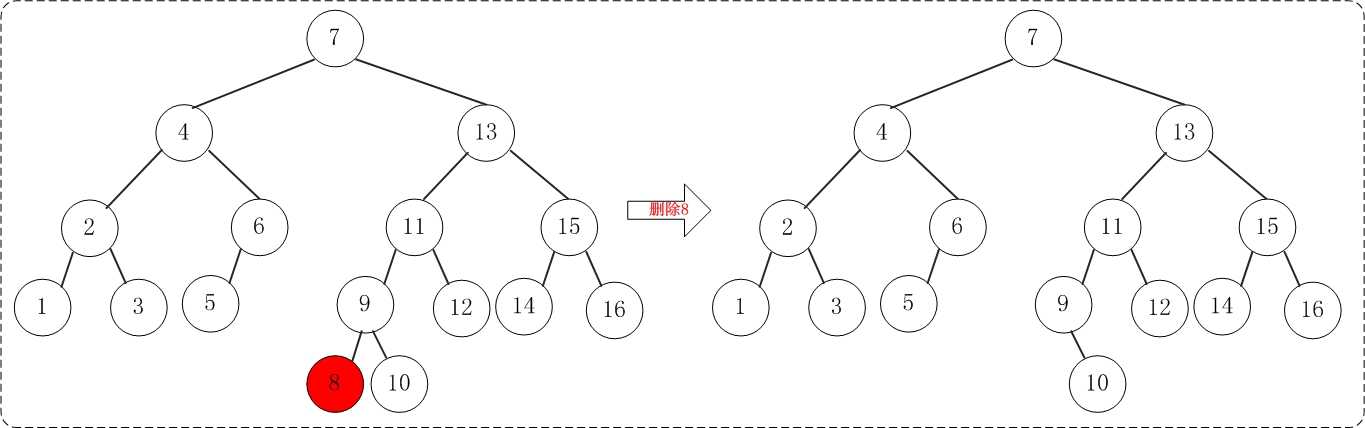
接着,删除节点8.删除节点8并不会造成AVL树的不平衡,所以不需要旋转,操作示意图如下:
程序运行结果如下:
== 依次添加: 3 2 1 4 5 6 7 16 15 14 13 12 11 10 8 9
== 前序遍历: 7 4 2 1 3 6 5 13 11 9 8 10 12 15 14 16
== 中序遍历: 1 2 3 4 5 6 7 8 9 10 11 12 13 14 15 16
== 后序遍历: 1 3 2 5 6 4 8 10 9 12 11 14 16 15 13 7
== 高度: 5
== 最小值: 1
== 最大值: 16
== 树的详细信息:
is root
is 7‘s left child
is 4‘s left child
is 2‘s left child
is 2‘s right child
is 4‘s right child
is 6‘s left child
is 7‘s right child
is 13‘s left child
is 11‘s left child
is 9‘s left child
is 9‘s right child
is 11‘s right child
is 13‘s right child
is 15‘s left child
is 15‘s right child
== 删除根节点: 8
== 高度: 5
== 中序遍历: 1 2 3 4 5 6 7 9 10 11 12 13 14 15 16
== 树的详细信息:
is root
is 7‘s left child
is 4‘s left child
is 2‘s left child
is 2‘s right child
is 4‘s right child
is 6‘s left child
is 7‘s right child
is 13‘s left child
is 11‘s left child
is 9‘s right child
is 11‘s right child
is 13‘s right child
is 15‘s left child
is 15‘s right child
AVL之C++实现
标签:std fine 树节点 实现 完成 href 函数 out nim
原文地址:https://www.cnblogs.com/wuyepeng/p/9750025.html























