贪心算法及其理论依据——拟阵
2021-05-16 06:29
标签:auto 安全性 递归算法 不能 size 赫夫曼 贪心算法 贪婪 font 贪心算法主要采用局部最优的解决问题的策略,但是在很多时候都不能达到全局最优的效果,那么什么时候使用贪心算法能够得到全局最优呢?就此引出拟阵的概念。 贪心算法中,我们所做的总是当前看似最佳的选择,然后在解决经过贪心选择之后所出现的子问题。其作出的当前的选择可能要依赖于已经做出的所有选择,但不依赖于未做出的选择或子问题的解。贪心算法采取的贪婪策略往往是自顶向下的。核心所在就是要证明每一步所做的贪心选择最终能产生一个全局最优解。 对于一个问题,如果它的一个最优解包含了其子问题的最优解,则称该问题具有最优子结构(最优子结构的证明采用部分替换法)。 拟阵理论是组合优化的一个分支。拟阵理论并不是因为贪心算法而引入,但是却是贪心算法的强力辅助。拟阵理论不能完全覆盖所有的贪心算法(如赫夫曼编码问题),但它可以覆盖大多数具有实际意义的情况。 在问题模型满足拟阵结构的情况下,贪心策略总是能够得到最优解。 贪心算法及其理论依据——拟阵 标签:auto 安全性 递归算法 不能 size 赫夫曼 贪心算法 贪婪 font 原文地址:https://www.cnblogs.com/zhangzefei/p/9749735.html贪心算法的一般步骤
贪心选择
最优子结构
设计贪心算法的一般步骤
拟阵
拟阵的概念
定义1:子集系统的优化问题

定义2:拟阵


贪心算法
定义4:拟阵的权函数
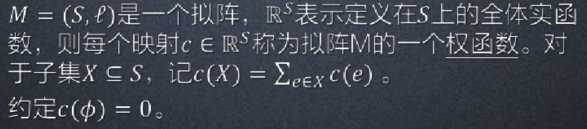
定义5:拟阵的最大权独立集问题

拟阵的性质
定义3:独立子集

定理1

定理2

定理3

贪心算法


下一篇:转:JAVA守护线程