协同过滤推荐算法

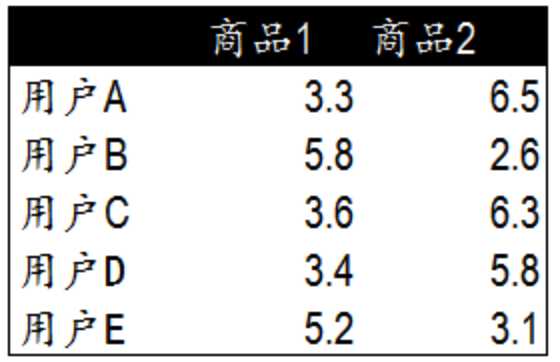
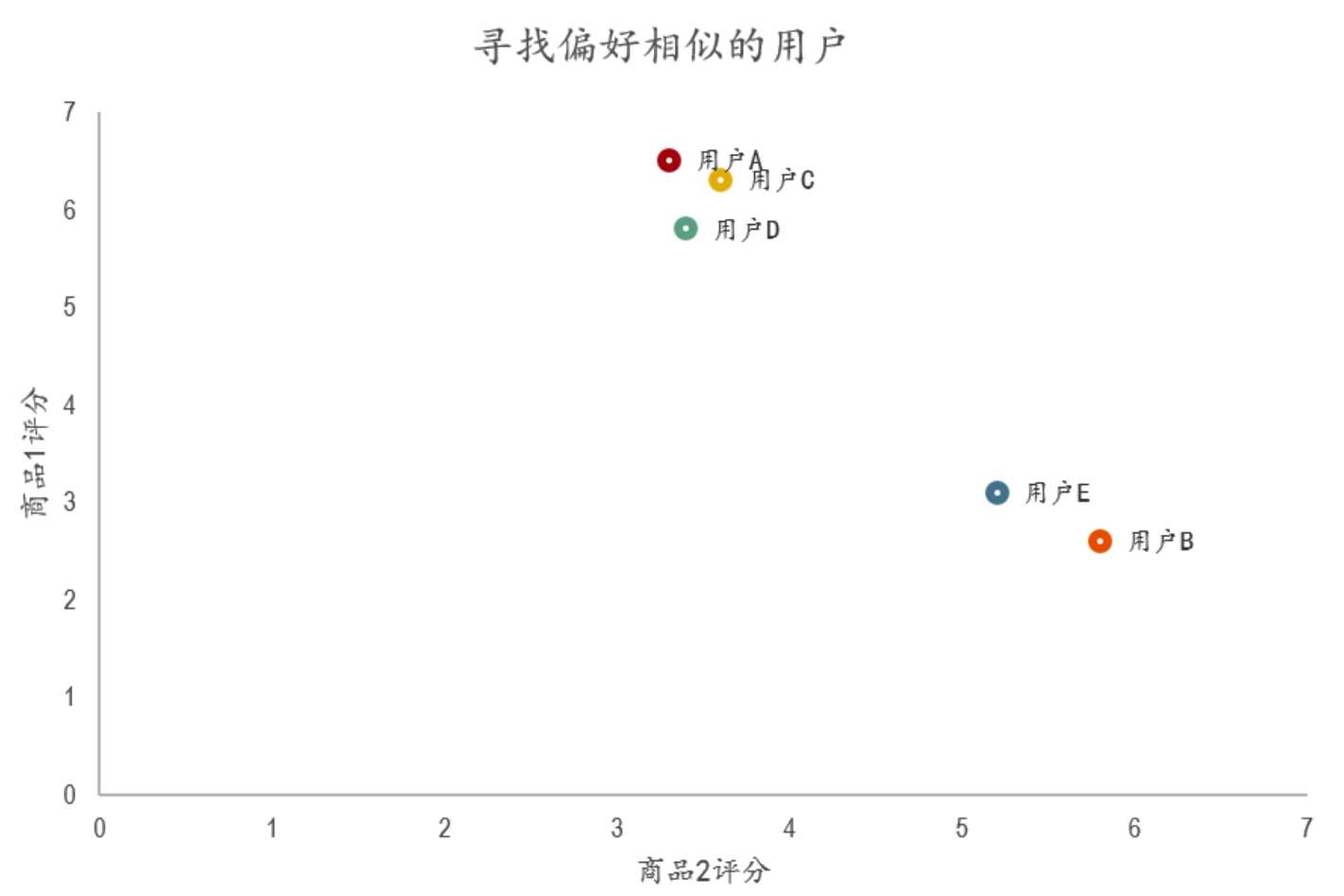
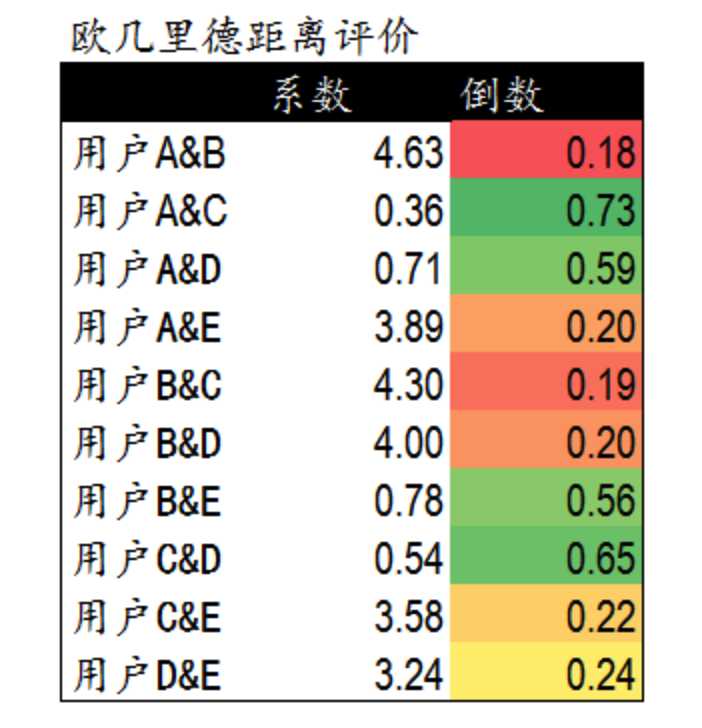
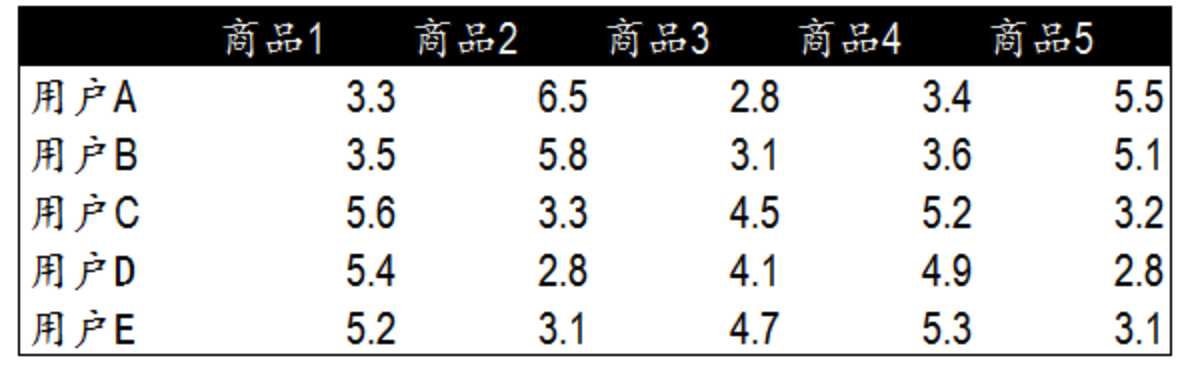
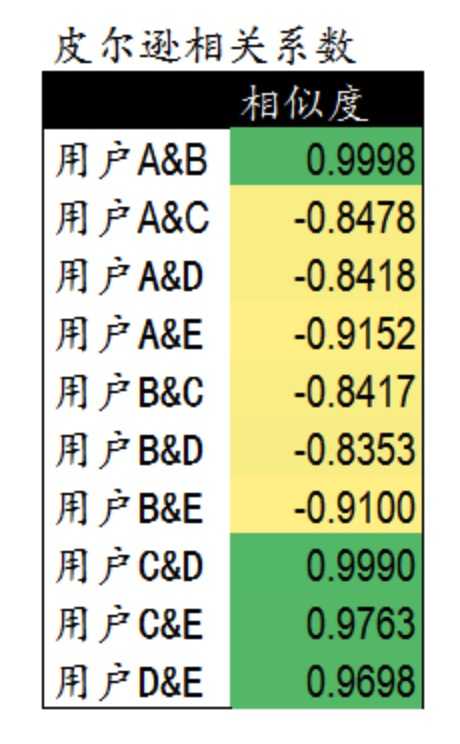
标签：3.4   需要   oat   简单   度量   朋友   图书   com   ora   

协同过滤推荐算法是诞生最早，并且较为著名的推荐算法。主要的功能是预测和推荐。算法通过对用户历史行为数据的挖掘发现用户的偏好，基于不同的偏好对用户进行群组划分并推荐品味相似的商品。协同过滤推荐算法分为两类，分别是基于用户的协同过滤算法(user-based collaboratIve filtering)，和基于物品的协同过滤算法(item-based collaborative filtering)。简单的说就是：人以类聚，物以群分。下面我们将分别说明这两类推荐算法的原理和实现方法。

1.基于用户的协同过滤算法(user-based collaboratIve filtering)

　　基于用户的协同过滤算法是通过用户的历史行为数据发现用户对商品或内容的喜欢(如商品购买，收藏，内容评论或分享)，并对这些喜好进行度量和打分。根据不同用户对相同商品或内容的态度和偏好程度计算用户之间的关系。在有相同喜好的用户间进行商品推荐。简单的说就是如果A,B两个用户都购买了x,y,z三本图书，并且给出了5星的好评。那么A和B就属于同一类用户。可以将A看过的图书w也推荐给用户B。

1.1寻找偏好相似的用户

　　我们模拟了5个用户对两件商品的评分，来说明如何通过用户对不同商品的态度和偏好寻找相似的用户。在示例中，5个用户分别对两件商品进行了评分。这里的分值可能表示真实的购买，也可以是用户对商品不同行为的量化指标。例如，浏览商品的次数，向朋友推荐商品，收藏，分享，或评论等等。这些行为都可以表示用户对商品的态度和偏好程度。

从表格中很难直观发现5个用户间的联系，我们将5个用户对两件商品的评分用散点图表示出来后，用户间的关系就很容易发现了。在散点图中，Y轴是商品1的评分，X轴是商品2的评分，通过用户的分布情况可以发现，A,C,D三个用户距离较近。用户A(3.3 6.5)和用户C(3.6 6.3)，用户D(3.4 5.8)对两件商品的评分较为接近。而用户E和用户B则形成了另一个群体。

散点图虽然直观，但无法投入实际的应用，也不能准确的度量用户间的关系。因此我们需要通过数字对用户的关系进行准确的度量，并依据这些关系完成商品的推荐。

1.2欧几里德距离评价

　　欧几里德距离评价是一个较为简单的用户关系评价方法。原理是通过计算两个用户在散点图中的距离来判断不同的用户是否有相同的偏好。以下是欧几里德距离评价的计算公式。

　　通过公式我们获得了5个用户相互间的欧几里德系数，也就是用户间的距离。系数越小表示两个用户间的距离越近，偏好也越是接近。不过这里有个问题，太小的数值可能无法准确的表现出不同用户间距离的差异，因此我们对求得的系数取倒数，使用户间的距离约接近，数值越大。在下面的表格中，可以发现，用户A&C用户A&D和用户C&D距离较近。同时用户B&E的距离也较为接近。与我们前面在散点图中看到的情况一致。

1.3皮尔逊相关度评价

　　皮尔逊相关度评价是另一种计算用户间关系的方法。他比欧几里德距离评价的计算要复杂一些，但对于评分数据不规范时皮尔逊相关度评价能够给出更好的结果。以下是一个多用户对多个商品进行评分的示例。这个示例比之前的两个商品的情况要复杂一些，但也更接近真实的情况。我们通过皮尔逊相关度评价对用户进行分组，并推荐商品。

1.4皮尔逊相关系数

　　皮尔逊相关系数的计算公式如下:

结果是一个在-1与1之间的系数。该系数用来说明两个用户间联系的强弱程度。

　　相关系数的分类:

1. 0.8-1.0 极强相关
2. 0.6-0.8 强相关
3. 0.4-0.6 中等程度相关
4. 0.2-0.4 弱相关
5. 0.0-0.2 极弱相关或无相关

　　通过计算5个用户对5件商品的评分我们获得了用户间的相似度数据。这里可以看到用户A&B，C&D，C&E和D&E之间相似度较高。下一步，我们可以依照相似度对用户进行商品推荐。

这里同时给出计算皮尔逊系数的py脚本：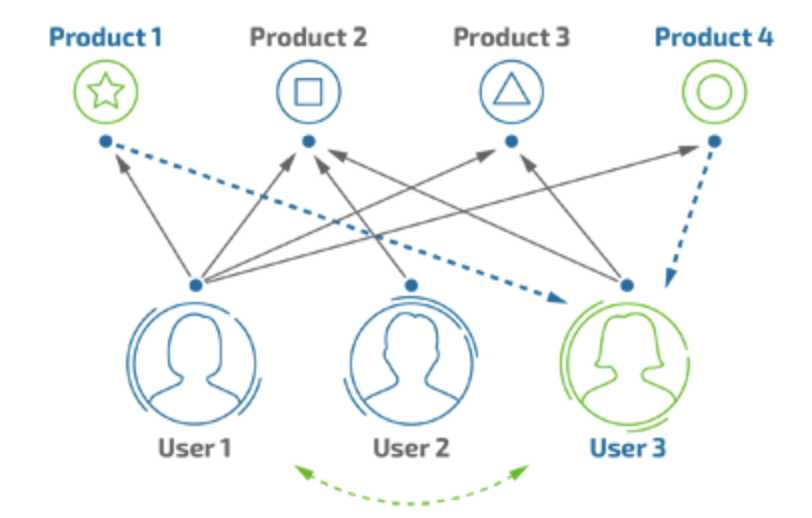

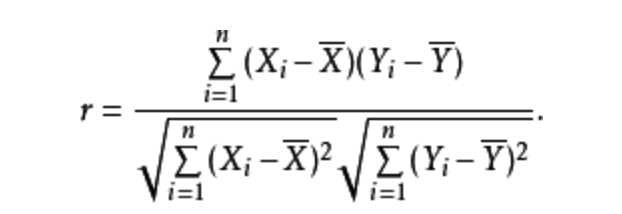
from math import sqrt


def multipl(a, b):
    sumofab = 0.0
    for i in range(len(a)):
        temp = a[i] * b[i]
        sumofab += temp
    return sumofab


def corrcoef(x, y):
    n = len(x)
    # 求和
    sum1 = sum(x)
    sum2 = sum(y)
    # 求乘积之和
    sumofxy = multipl(x, y)
    # 求平方和
    sumofx2 = sum([pow(i, 2) for i in x])
    sumofy2 = sum([pow(j, 2) for j in y])
    num = sumofxy - (float(sum1) * float(sum2) / n)
    # 计算皮尔逊相关系数
    den = sqrt((sumofx2 - float(sum1 ** 2) / n) * (sumofy2 - float(sum2 ** 2) / n))
    return num / den

x = [3.3, 6.5, 2.8, 3.4, 5.5]
y = [5.6, 3.3, 4.5, 5.2, 3.2]

print(corrcoef(x, y))

2、

协同过滤推荐算法

标签：3.4   需要   oat   简单   度量   朋友   图书   com   ora   

原文地址：https://www.cnblogs.com/xuelisheng/p/9747528.html