#002# 最大子数组问题
2021-05-18 03:28
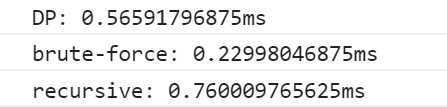
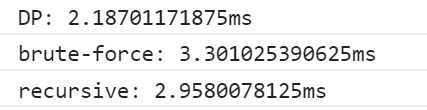
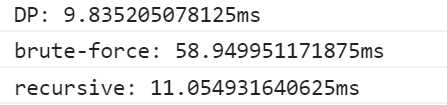
标签:and 动态规划 ssi 增加 tar OLE copy cas 分享 js代码: 数组长度为20实测(各跑100次)↓ 数组长度为100实测(各跑100次)↓ 数组长度为500实测(各跑100次)↓ #002# 最大子数组问题 标签:and 动态规划 ssi 增加 tar OLE copy cas 分享 原文地址:https://www.cnblogs.com/xkxf/p/9745248.html class MaxSub {
// 解法1:动态规划 -- O(n)
static solve(arr, start, end) {
let s = []; // s[n]保存arr[start:n+1]的最大子段和
let b = []; // b[n]保存由从arr[n]开始到arr[start]的逆向最大和
s[start] = {
sum: arr[start],
start: start,
end: start + 1
}; // 当数组只有一个元素的时候,最大子段和只能是这个元素
b[start] = CommonUtil.lightCopy(s[start]);
for (let i = start + 1; i != end; ++i) {
// b[i] = max(b[i-1]+arr[i], arr[i])
if (b[i - 1].sum + arr[i] > arr[i]) {
b[i] = CommonUtil.lightCopy(b[i - 1]);
b[i].sum += arr[i];
} else {
b[i] = {sum: arr[i], start: i};
}
b[i].end = i + 1;
// s[i] = max(s[i-1], b[i])
s[i] = CommonUtil.lightCopy(
s[i - 1].sum >= b[i].sum ? s[i - 1] : b[i]
);
}
// 证明:假设s[n]是截至arr[n]的最大子段和(包括arr[n])
// 当考察s[n+1]时,相当于往原序列添加一个新元素arr[n+1]
// 结果是生成了arr[0..n+1],arr[1..n+1]等n+1个新序列
// 我们选取这些新序列中最大的,即从arr[n+1]开始的"逆向最大和",
// 与旧序列的最大子段和s[n]比较,s[n+1]取两者中更大的一个
// (其实就是在新和旧之间决策),因为考虑了所有可能的情况,
// 并且是大中选大,所以s[n+1]是截至arr[n+1]的最大子段和。
// 思路:先考虑一个元素的情况,显然最大子段和只能是那个元素
// 然后考虑2个元素的情况(在原基础上增加1个),要么仍是第
// 一个元素,要么就是逆向最大和,继续增加元素考虑,发现都是
// 反复在做同样的决策....
return s[end - 1];
}
// 解法2:暴力求解 -- O(n^2)
static solve2(arr, start, end) {
let result = {
sum: -Infinity,
start: start,
end: end
};
for (let i = start; i != end; ++i) {
let temp = {
sum: 0,
start: i
};
for (let j = i; j != end; ++j) {
temp.sum += arr[j];
temp.end = j + 1;
if (temp.sum > result.sum) {
result = CommonUtil.lightCopy(temp);
}
}
}
return result;
}
// 解法3:递归(分治) -- O(nlgn),来自算法导论
static solve3(arr, start, end) {
function findMaxCrossingSubarray(arr, start, mid, end) {
let leftSum = -Infinity;
let sum = 0;
let maxLeft; // 开始下标
for (let i = mid - 1; i >= start; --i) {
sum = sum + arr[i];
if (sum > leftSum) {
leftSum = sum;
maxLeft = i;
}
}
let rightSum = -Infinity;
sum = 0;
let maxRight; // 结束下标
for (let j = mid; j != end; ++j) {
sum = sum + arr[j];
if (sum > rightSum) {
rightSum = sum;
maxRight = j;
}
}
return {
sum: leftSum + rightSum,
start: maxLeft,
end: maxRight + 1
};
}
if (start + 1 == end) { // base case
return {
sum: arr[start],
start: start,
end: end
};
} else {
let mid = Math.floor((start + end) / 2);
let leftResult = MaxSub.solve3(arr, start, mid);
let rightResult = MaxSub.solve3(arr, mid, end);
let crossResult = findMaxCrossingSubarray(arr, start, mid, end);
let finalResult = {
sum: -Infinity,
};
if (leftResult.sum > finalResult.sum) finalResult = CommonUtil.lightCopy(leftResult);
if (rightResult.sum > finalResult.sum) finalResult = CommonUtil.lightCopy(rightResult);
if (crossResult.sum > finalResult.sum) finalResult = CommonUtil.lightCopy(crossResult);
return finalResult;
}
}
static run(data) {
let arr = CommonUtil.handleData(data);
let result = MaxSub.solve(arr, 0, arr.length);
// console.log(result);
console.log(arr.slice(result.start, result.end));
console.log(`max_sum = ${result.sum}`);
}
}
下一篇:python初识一