最短路径(Dijskra算法)
标签:code dmi end 合数 clu else stack rom display
声明:图片及内容基于:https://www.bilibili.com/video/BV16C4y1H7Zc?from=articleDetail
最短路径
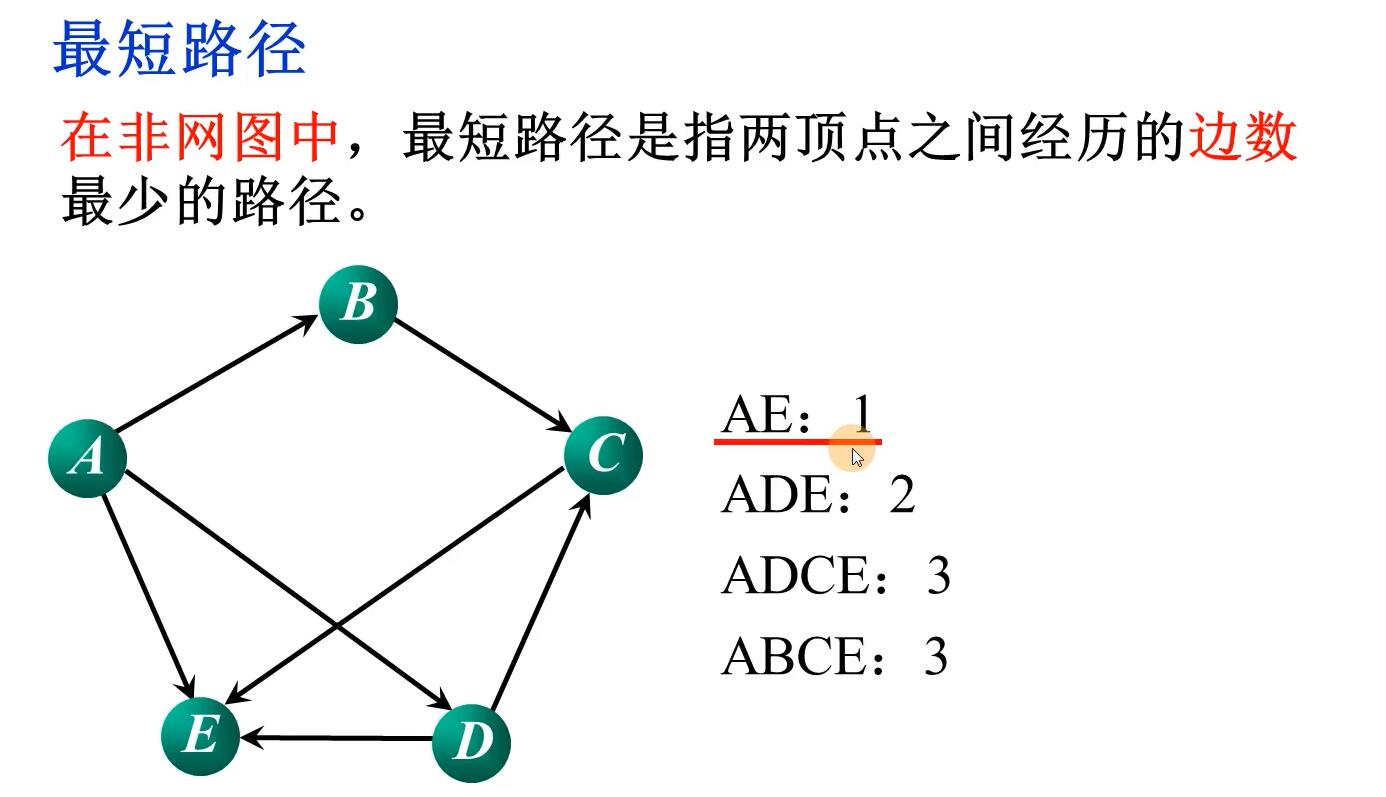
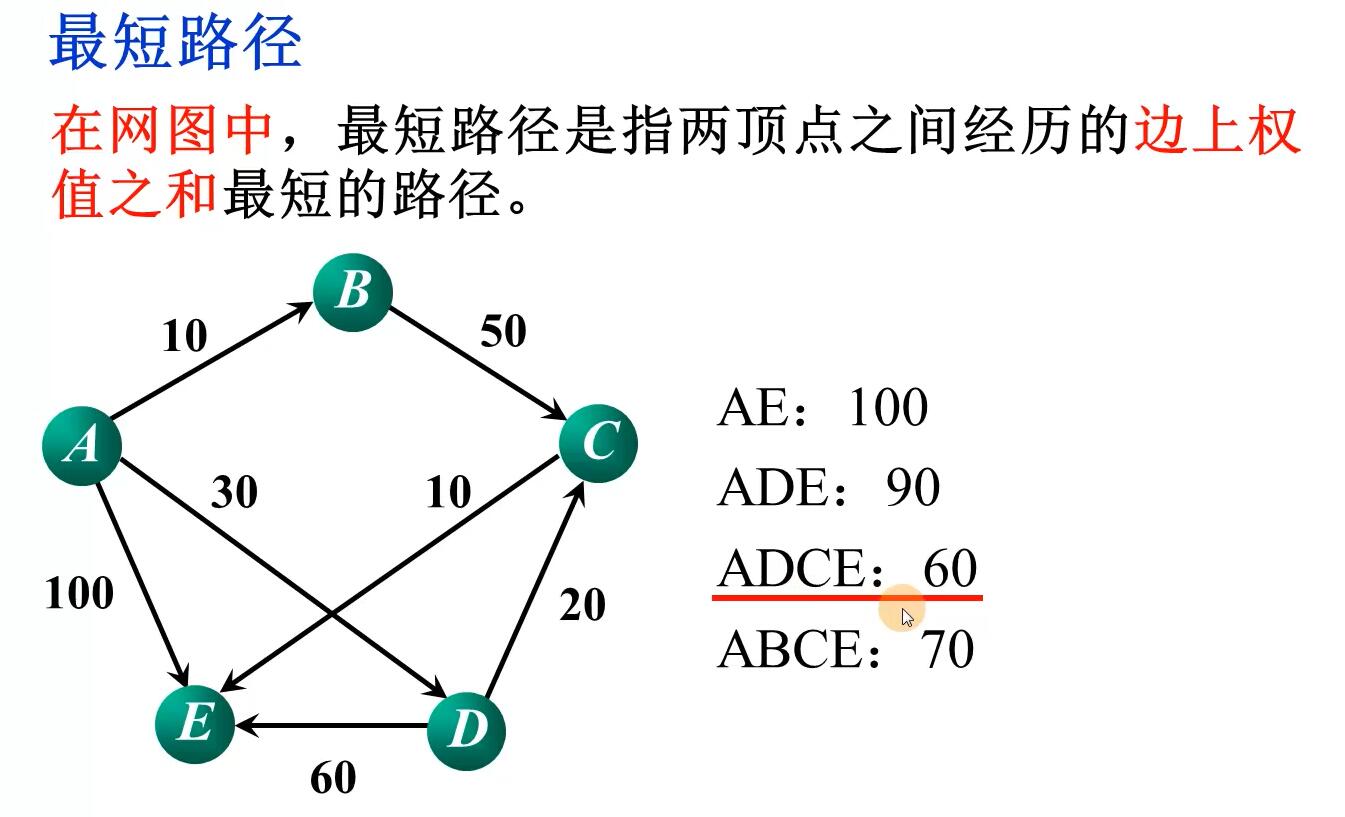

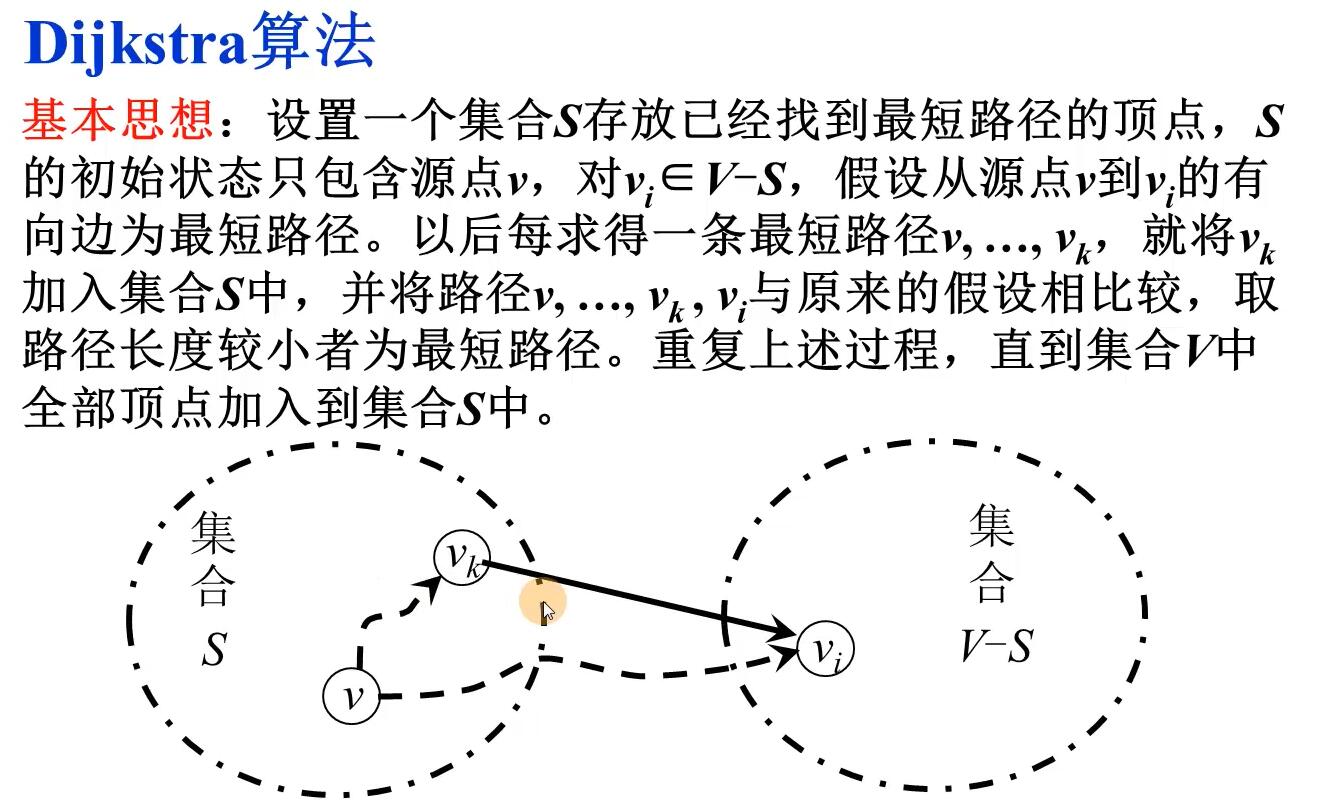
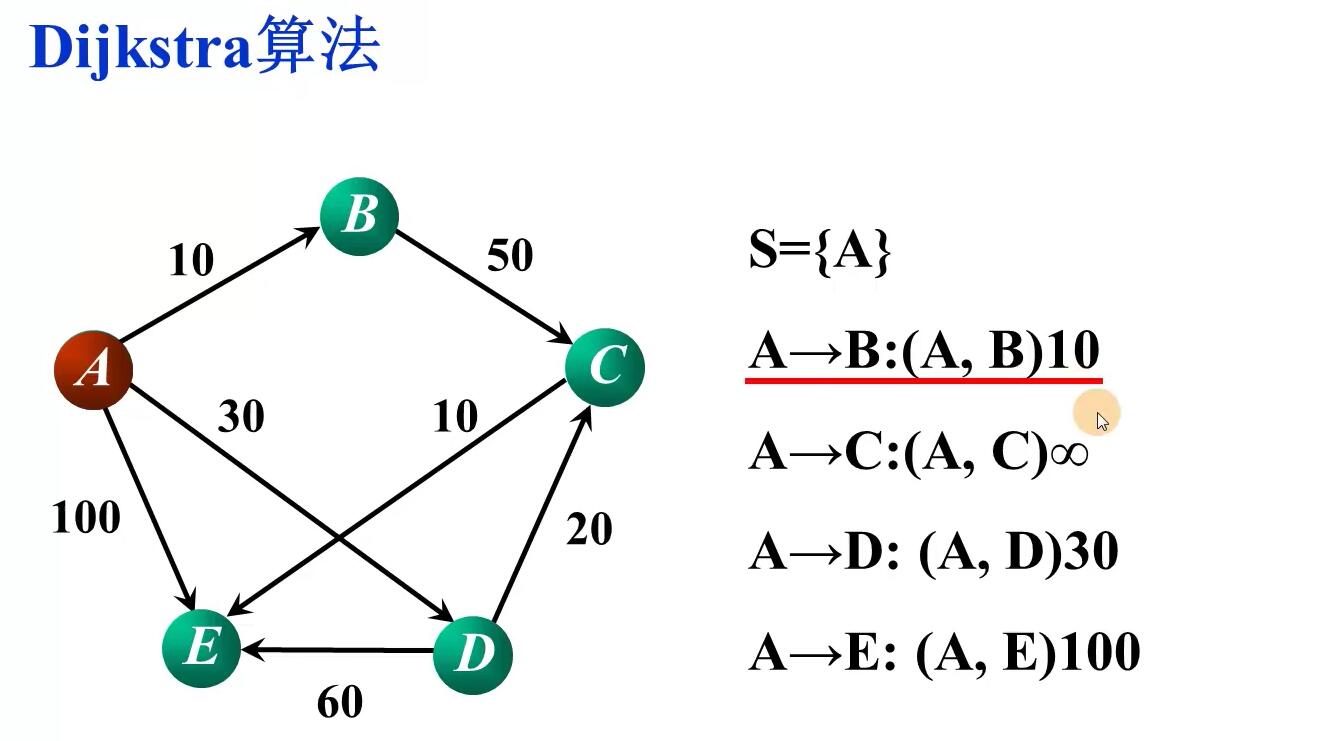
Dijkstra算法
原理
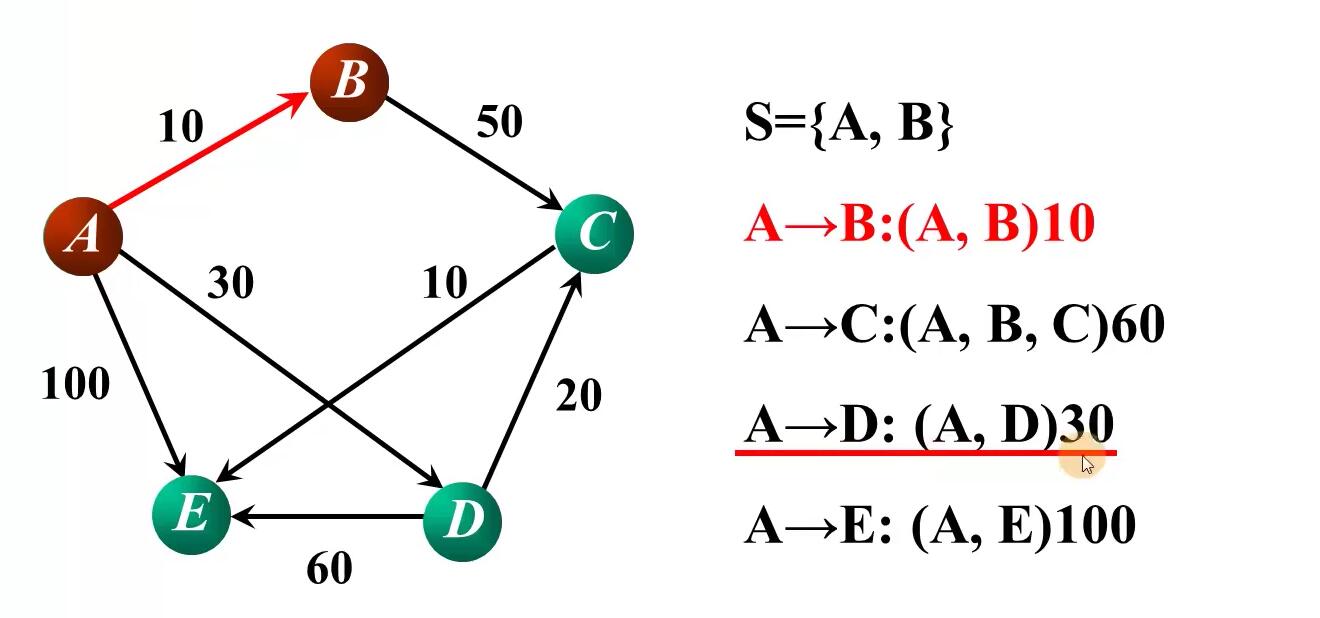
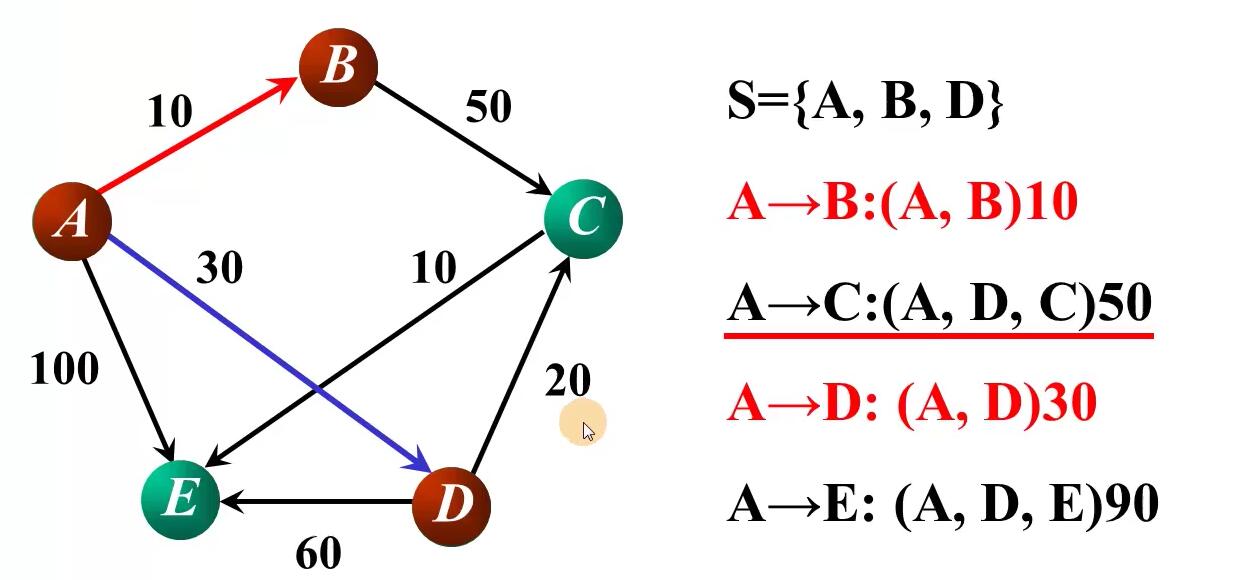
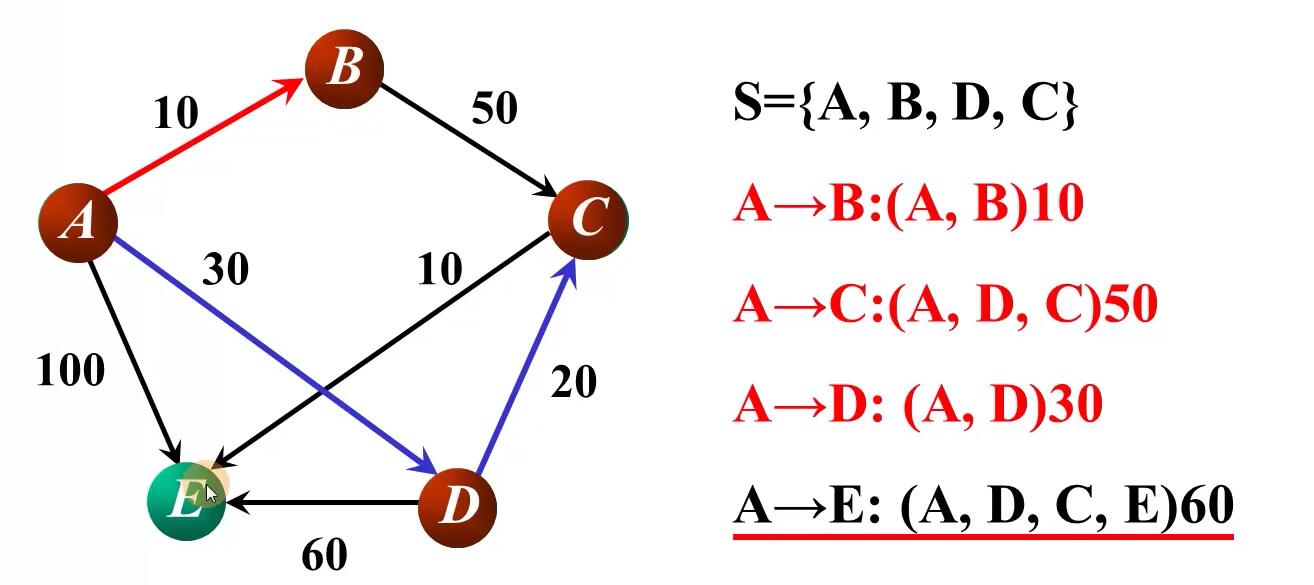
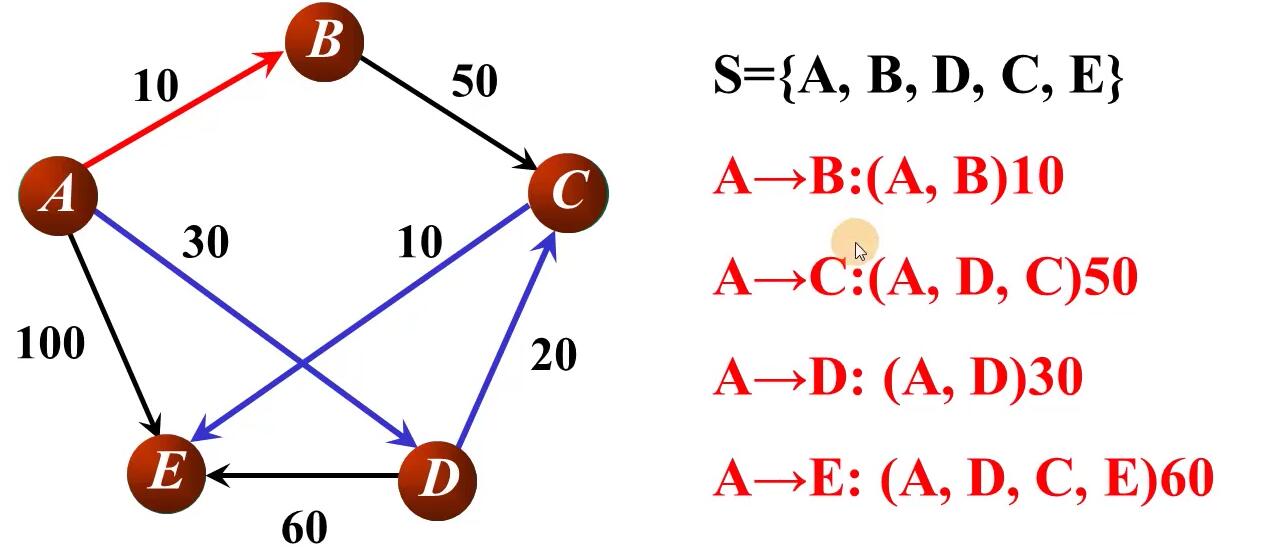
数据结构


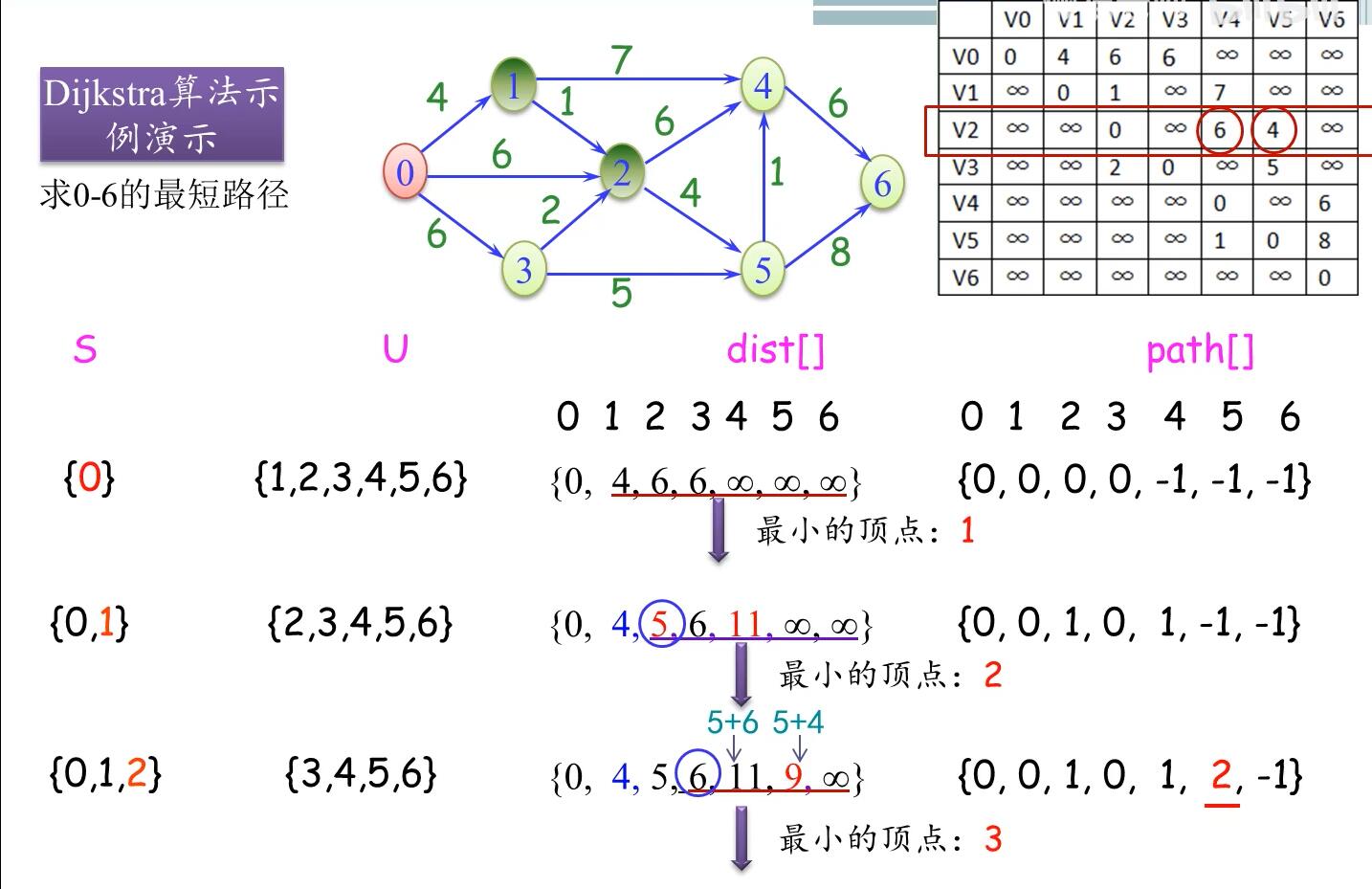

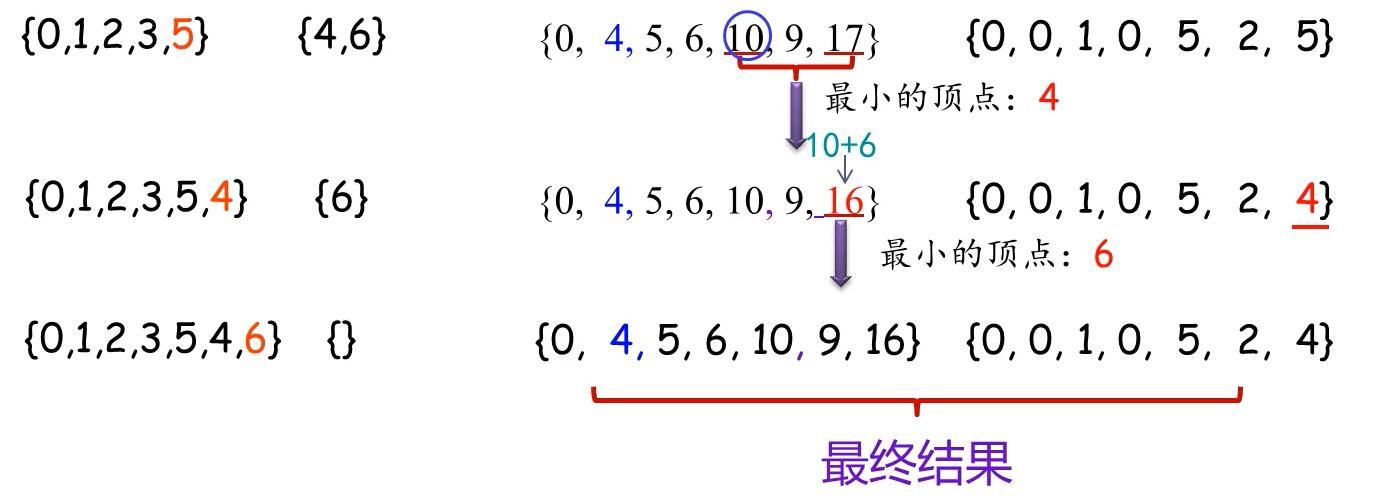
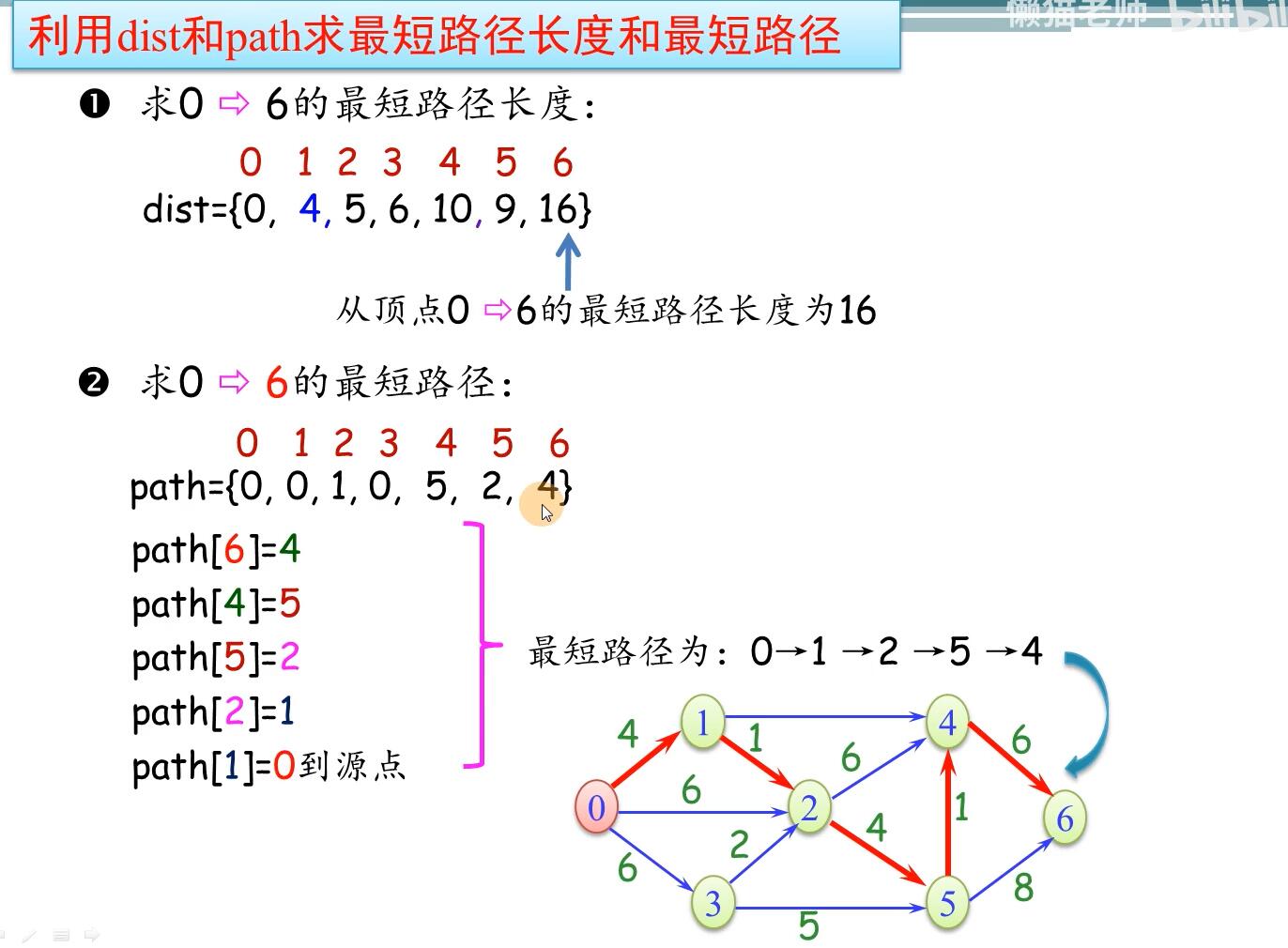
核心代码

findMinDist()
int MGraph::findMinDist(){
int length=INFINIT;
for(int i=0;i){
if(s[i]==0){
if(length>dist[i]&&dist[i]!=0&&dist[i]!=INFINIT){
length=i; //注意记录的是下标,我原来写成length=dist[i]了,太惨了
}
}
}
return length;
}
displayPath()
void MGraph::displayPath(){ //打印最短路径
for(int i=0;i){
if(i==startV) cout//起点直接打印
if(i!=startV){ //其他结点
int tmp=i;
stackint> s; //逆序输出使用栈
while(tmp!=startV){
s.push(path[tmp]);
tmp=path[tmp];
}
while(!s.empty()){
cout"->";
s.pop();
}
couti;
coutendl;
}
}
}
Dijkstra(int startV)
void MGraph::Dijkstra(int startV){
this->startV=startV; //别忘了,startV也是MGraph的数据成员
for(int i=0;i){
dist[i]=arc[startV][i]; //dist数组初始化
if(dist[i]!=INFINIT) //path数组初始化
path[i]=startV;
else
path[i]=-1;
}
for(int i=0;i//s数组初始化
s[i]=0;
s[startV]=1; //startV放入集合
int num=1; //集合数据个数1
while(numvertexNum){
int min=findMinDist(); //min是当前dist数组中最短路径的下标,前提是s[i]=0,即查找的
//是集合的补集元素
s[min]=1; //min放入集合
for(int i=0;i//更新dist和path数组
if(s[i]==0&&(dist[i]>dist[min]+arc[min][i])){
dist[i]=dist[min]+arc[min][i];
path[i]=min;
}
}
num++;
}
displayPath(); //显示全部最短路径
}
完整代码
#include#define MAX 50
#define INFINIT 65535
#include using namespace std;
class MGraph{
private:
int vertexNum,arcNum; //顶点数,边数
int arc[MAX][MAX]; //邻接矩阵
int vertex[MAX]; //顶点信息
int dist[MAX]; //记录单源到每个点的最短路径的长度
int path[MAX]; //记录当前从某点到某点的最短路径,存放的是某点起点的顶点信息
int s[MAX]; //记录已经确定的最短路径的结点集合
int startV;
public:
MGraph(int v[],int n,int e);
void display();
void Dijkstra(int startV);
int findMinDist();
void displayPath();
void displayDistPathS();
};
void MGraph::displayDistPathS(){
cout"dist:"endl;
for(int i=0;i){
cout" ";
}
coutendl;
cout"path:"endl;
for(int i=0;i){
cout" ";
}
coutendl;
cout"S:"endl;
for(int i=0;i){
cout" ";
}
coutendl;
}
MGraph::MGraph(int v[],int n,int e){ //n是顶点数,e是边数
vertexNum=n;
arcNum=e;
for(int i=0;i){
vertex[i]=v[i];
}
for(int i=0;i//初始化邻接矩阵
for(int j=0;j){
if(i==j) arc[i][j]=0;
else arc[i][j]=INFINIT;
}
}
int vi,vj,w;
for(int i=0;i){
cout"请输入有向边的两个顶点和这条边的权值"endl;
cin>>vi>>vj>>w; //输入边依附的两个顶点的编号 和权值
arc[vi][vj]=w; //有边标志
}
}
void MGraph::display(){
cout"邻接矩阵:"endl;
for(int i=0;i){
for(int j=0;j){
if(arc[i][j]==INFINIT)
cout"∞""\t";
else cout"\t";
}
coutendl;
}
coutendl;
cout"结点信息:"endl;
for(int i=0;i){
cout" ";
}
coutendl;
}
int MGraph::findMinDist(){
int length=INFINIT;
for(int i=0;i){
if(s[i]==0){
if(length>dist[i]&&dist[i]!=0&&dist[i]!=INFINIT){
length=i; //注意记录的是下标,我原来写成length=dist[i]了,太惨了
}
}
}
return length;
}
void MGraph::displayPath(){ //打印最短路径
for(int i=0;i){
if(i==startV) cout//起点直接打印
if(i!=startV){ //其他结点
int tmp=i;
stackint> s; //逆序输出使用栈
while(tmp!=startV){
s.push(path[tmp]);
tmp=path[tmp];
}
while(!s.empty()){
cout"->";
s.pop();
}
couti;
coutendl;
}
}
}
void MGraph::Dijkstra(int startV){
this->startV=startV; //别忘了,startV也是MGraph的数据成员
for(int i=0;i){
dist[i]=arc[startV][i]; //dist数组初始化
if(dist[i]!=INFINIT) //path数组初始化
path[i]=startV;
else
path[i]=-1;
}
for(int i=0;i//s数组初始化
s[i]=0;
s[startV]=1; //startV放入集合
int num=1; //集合数据个数1
while(numvertexNum){
int min=findMinDist(); //min是当前dist数组中最短路径的下标,前提是s[i]=0,即查找的
//是集合的补集元素
s[min]=1; //min放入集合
for(int i=0;i//更新dist和path数组
if(s[i]==0&&(dist[i]>dist[min]+arc[min][i])){
dist[i]=dist[min]+arc[min][i];
path[i]=min;
}
}
num++;
}
displayPath(); //显示全部最短路径
}
int main(){
int n,e;
int v[MAX];
cout"请输入顶点数和边数"endl;
cin>>n>>e;
cout"请输入顶点信息"endl;
for(int i=0;i){
cin>>v[i];
}
cout"请输入起点:"endl;
int t;
cin>>t;
MGraph mgraph(v,n,e);
mgraph.display();
mgraph.Dijkstra(t);
mgraph.displayDistPathS();
return 0;
}
输入:
7 12
0 1 2 3 4 5 6
0
0 1 4
0 2 6
0 3 6
1 2 1
1 4 7
2 4 6
2 5 4
3 2 2
3 5 5
4 6 6
5 4 1
5 6 8
输出:
邻接矩阵:
0 4 6 6 ∞ ∞ ∞
∞ 0 1 ∞ 7 ∞ ∞
∞ ∞ 0 ∞ 6 4 ∞
∞ ∞ 2 0 ∞ 5 ∞
∞ ∞ ∞ ∞ 0 ∞ 6
∞ ∞ ∞ ∞ 1 0 8
∞ ∞ ∞ ∞ ∞ ∞ 0
结点信息:
0 1 2 3 4 5 6
0
0->1
0->1->2
0->3
0->1->4
0->1->2->5
0->1->4->6
dist:
0 4 5 6 11 9 17
path:
0 0 1 0 1 2 4
S:
1 1 1 1 1 1 1
最短路径(Dijskra算法)
标签:code dmi end 合数 clu else stack rom display
原文地址:https://www.cnblogs.com/gonghr/p/14613393.html
评论















