算法--动态规划
2021-06-07 00:04
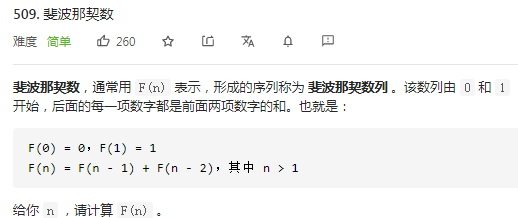
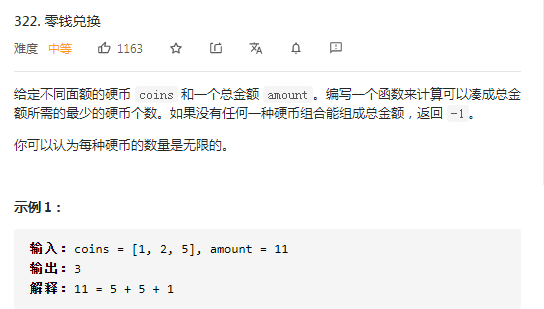
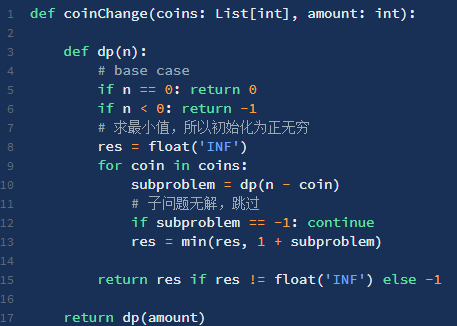
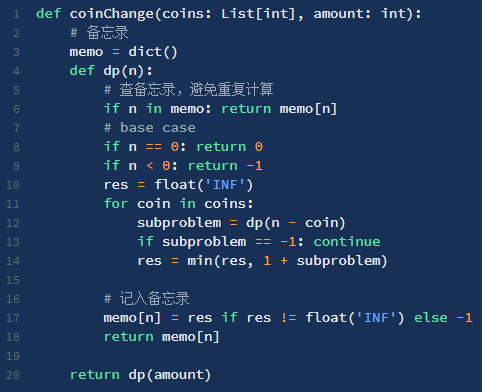
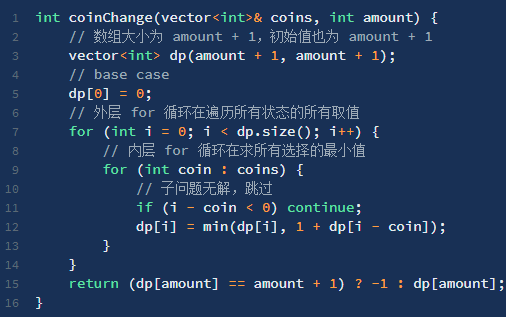
标签:运算 时间 返回 cas 复杂度 sum ase 自底向上 参数 一、概念 1、三要素 2、(列状态转移方程)步骤 明确初始条件base case、明确状态、明确选择、定义dp数组/函数 二、斐波那契数列 1、原始暴力递归 重复运算--重叠子问题 递归的时间复杂度 2、带备忘录的递归(自顶向下) 3、dp数组的迭代解法(自底向上) 4、状态压缩,空间复杂度变为O(1) 三、凑零钱问题 1、暴力递归 符合最优子结构,硬币不限数量。与真实考试拿第一不同 步骤: 明确初始条件base case(目标金额amount为0,硬币为0)、 明确状态(amount不断变小直到base case)、 明确选择(硬币面值)、 定义dp数组/函数(自顶向下的函数参数是状态变化量amount,返回值为要计算的量) 2、带备忘录的递归 3、dp数组的迭代解法(自底向上) 此题不适合用Java语言dp函数自顶向下求 算法--动态规划 标签:运算 时间 返回 cas 复杂度 sum ase 自底向上 参数 原文地址:https://www.cnblogs.com/liujinhui/p/14594448.html
重叠(+备忘录)子问题、最优子结构、状态转移方程
class Solution {
//初始化备忘录为0
int[] mome;
public int fib(int n) {
mome = new int[n+1];
if(n return 0;
return comput(mome,n);
}
public int comput(int []mome,int n){
if(n == 1 || n == 2) return 1;
if(mome[n]!=0) return mome[n];
mome[n] = comput(mome, n-1) + comput(mome, n-2);
return mome[n];
}
}
class Solution {
public int fib(int n) {
if(n return 0;
if(n == 1 || n ==2) return 1;
int[] arr = new int[n+1]; //Java默认将数组初始化为0
arr[1] = arr[2] = 1;
for(int i = 3; i ){
arr[i] =arr[i-1] +arr[i-2];
}
return arr[n];
}
}
class Solution {
public int fib(int n) {
if(n return 0;
if(n==1 || n==2) return 1;
int prev=1,curr=1,sum;
for(int i=3;i){
sum = prev + curr;
prev = curr;
curr = sum;
}
return curr;
}
}
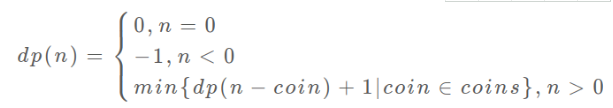
class Solution {
public int coinChange(int[] coins, int amount) {
if(amount return -1;
int[] dp = new int[amount+1];
Arrays.fill(dp,amount+1);
dp[0] = 0;
for(int i = 0; i ){
for(int coin:coins){
if(i -coin continue;
dp[i] = Math.min(dp[i],1+dp[i-coin]);
}
}
return dp[amount]==amount+1?-1:dp[amount];
}
}