[APIO2016]烟火表演
2021-06-20 01:04
标签:image color getch www wap stream += int 描述 题目描述 https://www.lydsy.com/JudgeOnline/problem.php?id=4585 题解 这题太神了。 我们可以先列出一个dp方程,dp[x][d]表示x节点到所有叶子的距离的d时的代价。 结论1:对于每个点来说,这个dp数组为二维平面上是一个下凸函数。 证明:对于叶子来说一定成立,在w[x]处为0,然后小于w[x]的部分斜率为-1,大与w[x]的部斜率为1。 对于非叶子节点 ,它的函数时有儿子们加起来的,也成立。 然后我们考虑一个点如何向父亲转移。 这是要分四种情况,假设当前节点的斜率为0的部分为L~R。 x
因为边权不能为负,所以我们只能从小的地方往大的地方转移。 比如这个蓝点,它只能从它以及前面的地方转移,但从自己转移时最优的。 x>=L&&x
在L处答案为f(L)+w,没往右动一格代价会-1。 x>=L+w[u]&&x
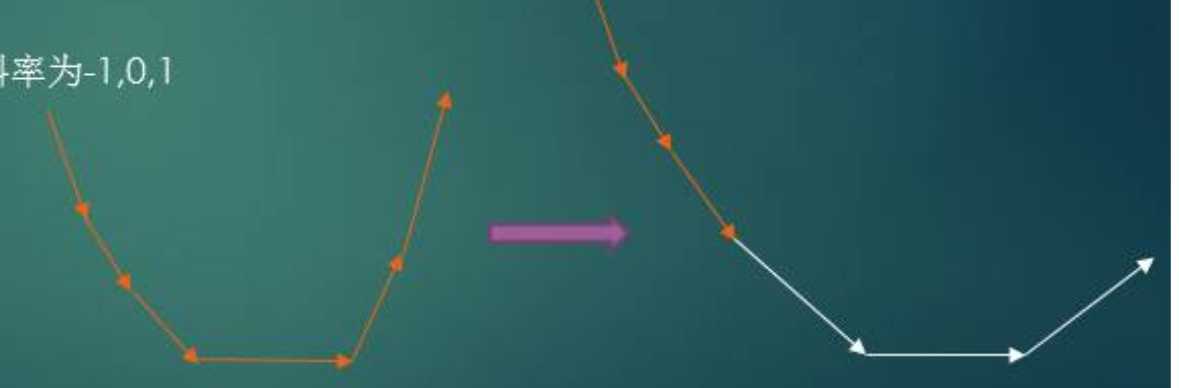
这个相当于直接转移了,没有代价。 x>=R+w[u] f‘(x)=f(x)+(x-R)-w 相当于是走过了,会产生代价。 我们发现转移大概长这样(继续盗图)。 我们把左边的点向上动一段后插入斜率为-1的线,再把斜率为0的部分向右平移,最后面是斜率为1的线。 然后这种操作就可以维护了。 思路大概就是只维护拐点,用一个可并堆,每次把右边的部分弹掉。 结论2:每次合并到一个非叶子节点时,斜率为0的线右边有n个点,n为该点的儿子数。 证明:因为最后那一块斜率一定为n(n个斜率为1的直线相加),然后往前经过一个拐点,斜率会-1。 然后把LR取出来做平移,再插回去,最后一直合并到1。 结论3:每经过一个拐点,斜率-1(其实它和上面的结论一个意思)。 然后就可以利用最后的拐点直接算答案了。 怎么算呢?我们把斜率>=0的直线弹掉,把前面的所有直线斜率+1,那么每条直线都会产生deltax的代价,总共有xn的代价,那我们就在答案里+xn,此时最后一条直线斜率为0,把它删掉。 然后一直做,最后得到的是f(0)-f(min),f(0)就是所有边权之和,那么f(min)就可以求出来了。 代码 [APIO2016]烟火表演 标签:image color getch www wap stream += int 描述 原文地址:https://www.cnblogs.com/ZH-comld/p/10269171.html
#include