算法学习(一)
标签:bsp ios .cpp 交换变量 过程 include 结束 模块化 实现
主要内容:
- 通过一道例题介绍算法设计的过程,及在设计与分析问题中运用的技巧及思想(c/c++实现)。
例题:求两个正整数的最大公约数。
- 数学模型:a,b > 0 的整数,求能c,c能整除a,b且a/c与b/c互质(没有公约数)。
- 问题分析:
- 分解因数法:a与b能共同整除的最大因数。
- 分解质因数法:a与b能共同整除的质因数相乘
- 短除法:所有公约数相乘。
- 辗转相除法:?
- 算法描述:
分解因数法:
- 分解因数法: ?source code
int a, b, flag;
input(a,b)
if(a>b)
a,b交换数值
for(从a循环递减,搜索最大的公因数)
if(能同时整除a,b即为公因数)
跳出循环;
print(flag);
- 算法说明:
- 定义flag用于标记公因数(也可直接用 a循环,这里便于理解定义flag变量)
- 比较a与b的大小,保证a为其中最小的数,方便下面进行循环(s-code中提供一种两变量交换数值的方法)
- 由于要求的是最大公因数,则采取倒序搜索减少搜索次数(即从大到小)
- 若要要求无限次键入a,b的值(即多组数据)且a或b等于0时结束输入,采用while(cin >> a >> b && a && b)输入模式:当while的条件语句中的任意条件为假停止循环(0为假,非0为真)
- 算法分析:最好是循环1次,最坏循环a次,则T(n)=1/n(1+.....+n)=(1/n)*n*(n+1)/2=1/2*n+1/2即时间复杂度为O(n).
分解质因数法:
- 分解质因数法:
#include
#includeusing namespace std;
bool pNumber(int n) //判断质数
{
for(int i = 2; i )
if(n%i == 0)
return false;
return true;
}
void exchange(int &x, int &y) //交换x,y的值
{
int temp = x;
x = y;
y = temp;
}
int main()
{
int a, b;
while(cin >> a >> b && a != 0 && b != 0){
int flag = 1;
if(a > b)
exchange(a, b);
for(int i = 2; i )
if(a%i == 0 && b%i == 0 && pNumber(i)){
flag *= i;
// cout
}
cout endl;
}
return 0;
}
- 算法说明:
- 采用模块化思想把main函数中的部分通用性的功能进行模块化处理(判断质数、交换变量值),自顶向下,逐步细分。
- 借助短路与(&&)的优点,减少循环的次数:pNumber()函数放在不同位置导致的循环次数不同if(a%i == 0 && b%i == 0 && pNumber(i)) if(pNumber(i) &&a%i == 0 && b%i == 0 )
- 算法分析:假设i能同时整除a,b的概率为p,则
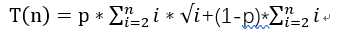 :O(n) = n^(5/2).
:O(n) = n^(5/2).
短除法:
-
- 短除法:
#include
#includeusing namespace std;
int main()
{
int a, b, t, i;
cin >> a >> b;
t = 1;
for(i = 2; i )
while(a%i == 0 && b%i == 0)
{
t = t*i;
a = a/i;
b = b/i;
}
cout endl;
return 0;
}
辗转相除法:
- 辗转相除法:
#include
#includeusing namespace std;
int main()
{
int a, b, c;
cin >> a >> b;
if(b == 0 || a == 0)
{
cout "data error!" endl;
return 0;
}
else
{
c = a % b;
while(c != 0)
{
a = b;
b = c;
c = a %b;
}
}
cout b;
return 0;
}
?source code------仅供参考
算法学习(一)
标签:bsp ios .cpp 交换变量 过程 include 结束 模块化 实现
原文地址:https://www.cnblogs.com/sunrisepeak/p/9652968.html
文章来自:
搜素材网的
编程语言模块,转载请注明文章出处。
文章标题:
算法学习(一)
文章链接:http://soscw.com/index.php/essay/96279.html
评论
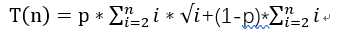 :O(n) = n^(5/2).
:O(n) = n^(5/2).