K-Means算法总结
2021-06-21 14:04
标签:第一个 分享 个数 随机 k-means 等于 k-means算法 算法 ima A、先确定k值,上图中k取2,随机然后选取质心为P1,P2 B、分别计算其它各点到这两个点的距离 C、选取距离近的点到相应的队列,如点离P1近,就把该点归到P1队列,如点离P2近,即把该点归到P2队列 D、根据公式, E、再次选距离近的点到相应的队列,并且重复上述D F、经过N次的迭代,队列不再变化,即表示算法收敛,聚类完成 二、用轮廓系数法验证聚类效果 a是Xi与同簇的其它样本的平均距离,称为凝聚度 b是Xi与最近簇中所有样本的平均距离,称为分离度 a越小,一个聚类的数据点越集中。b越大,一个聚类和另一个聚类分得越开 三、Calinski-Harabasz(CH系数):类别内部数据的协方差越小越好,类别之间的协方差越大越好,这样Calinski-Harabasz分数s会高,分数s高则聚类效果越好 m为训练集样本数,k为类别数。Bk为类别之间的协方差矩陈,Wk为类别内部数据的协方差矩陈,tr为矩陈的迹 类间协方差tr(Bk)越大越好,类内部协方差tr(Wk)越小越好,m样本数越多越好,k类别数越小越好,即各个簇的间距越大越好,各簇内部的数据越紧密越好,样本数越多越好,即数据量越多越好,划分的簇个数越少越好, Wk为类别内部数据的协方差矩阵,tr为矩陈的迹,所以tr(Wk)为类别内部数据的协方差矩阵的迹 四、聚类分类: 硬聚类:即每一个数据只能被归为一类,即每一个数据都会100%被确定 软聚类:每一个样本以一定的概率被分到某一类中 五、算法优化: 四种硬聚类优化算法(K-means++,二分K-Means,ISODATA,Kernel K-means) 1、K-means++:中心思想为选取聚类中心不再采用随机选取的方法,而是选取离当前质心越远的那个点作为新的质心,(即选取的第一个质心和第二个质心越远越好),离得越远的点会有更大的概率被选成新的质心 2、ISODATA:类别数目会动态变化(无需深入学习),即类别数会随机应变 3、Kernel K-means:将每个样本进行投射到高维空间去处理,将处理后的数据用K-means算法进行聚类 4、二分K-means:首先将所有点作为一个簇,然后将该簇一分为二。之后选择SSE最大的簇再划分成两个簇,如此循环下去,直到簇的数目等于用户给定的数目K为止(可以加速算法的执行速度,不受初始化问题的影响,每一步都保证误差最小) 六、误差平方和公式 SSE(Sum of Squares for Error)称作误差的平方和作为度量聚类质量的目标函数,反映每个样本各观测值的离散状况,又称为组内平方和或残差平方和。 SSE即为样本的聚类误差,代表聚类效果的好坏 K-Means算法总结 标签:第一个 分享 个数 随机 k-means 等于 k-means算法 算法 ima 原文地址:https://www.cnblogs.com/baoxuhong/p/9683476.html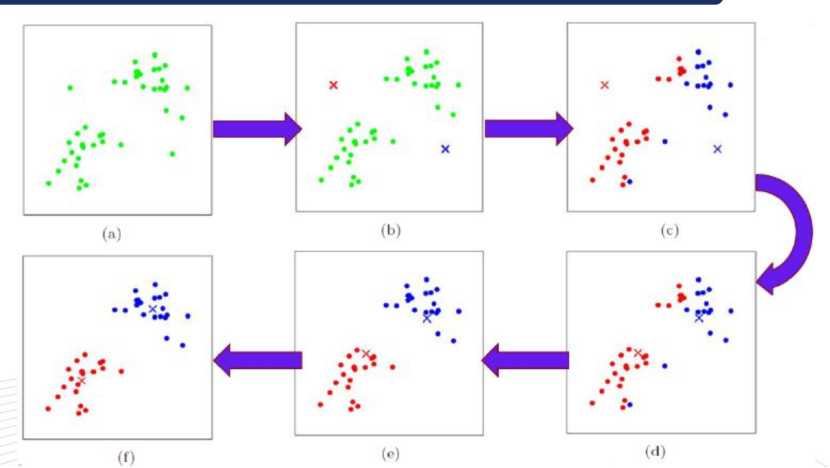
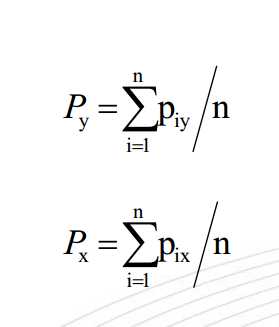 再取两个队列的虚拟质心,即两个队列中的所有点距离的平均值
再取两个队列的虚拟质心,即两个队列中的所有点距离的平均值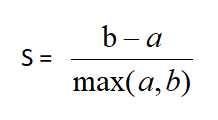 该值处于[-1,1]之间,值越大,聚类效果越好
该值处于[-1,1]之间,值越大,聚类效果越好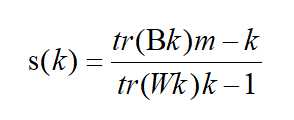
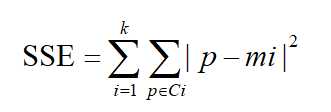
上一篇:Python web面试常见问题
下一篇:学习python课程第八天