(九)排序(选择、插入、希尔)
2021-06-22 20:04
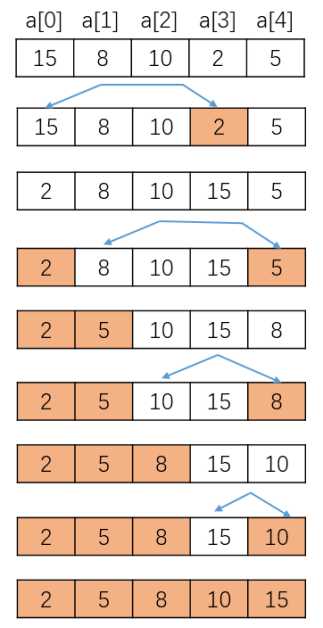
标签:对象 不能 inf length from sele author lsp 子类 目标 1) 使用下列方法将一个数组按升序排序:选择排序、插入排序和希尔排序 2) 使用插入排序将链式节点链按升序排序 3) 评估排序的效率,讨论不同方法的相对效率 目录 8.1 对数组进行排序的Java方法的组织 8.2 选择排序 8.2.1 迭代选择排序 8.2.2 递归选择排序 8.2.3 选择排序的效率 8.3 插入排序 8.3.1 迭代插入排序 8.3.2 递归插入排序 8.3.3 插入排序的效率 8.3.4 链式节点链的插入排序 8.4 希尔排序 8.4.1 算法 8.4.2 希尔排序的效率 8.5 算法比较 小结 用Java所实现的这些算法可以对任意的Comparable对象(即实现了接口Comparable的任意类的对象,故定义了方法compareTo)进行排序。 排序算法的效率很重要,特别是当涉及的数据量很大时。 8.1 对数组进行排序的Java方法的组织 将数组排序方法组织起来的一种方式是创建一个实现不同排序的静态方法的类。方法为数组中的对象定义泛型T。例如,可以将这种方法头表示如下: public static 数组a可以含有任意类的对象,n是待排序数组中项的个数。 对于要排序的数组,数组中的对象必须是Comparable的,所以T表示的类必须实现接口Comparable。为确保这个需求,在排序方法的方法头中,在返回类型的前面,使用 来替代 允许使用如下语句对T的子类的对象进行比较: T extends Comparable super T> 所以,方法sort的方法头应该写为: public static 8.2 选择排序 就数组a来说,选择排序找到数组中最小的项,将它与a[0]交换。然后,忽略a[0],排序找到下一个最小的项并交换到a[1],以此类推。注意,仅使用一个数组。通过将项与其他项进行交换来排序。 图1 使用选择排序将整数数组排成升序 8.2.1 迭代选择排序 Algorithm selectionSort(a, n) // 对数组a中的前n项进行排序 for (index = 0; index
indexOfNextSmallest = a[index], a[index+1], …, s[n - 1]中最小值的下标 交换a[index]和a[indexOfNextSmallest]的值 // 断言:a[0]≤a[1]≤…≤a[index],且它们是原数组项中的最小项 // 其余的数组项从a[index+1]开始 } 注意,在最后一次迭代中,虽然数组的最后一项在a[n-2]中,但index的值是n-2。 swap方法只用Object作为这些项的类型:交换数组中的项没有调用方法compareTo。 8.2.2 递归选择排序 Algorithm selectionSort(a, first, last) // 递归地排序数组项a[first]到a[last]。 if (first indexOfNextSmallest = a[first], a[first+1],…, a[last]中最小值的下标 交换a[first]和a[indexOfNextSmallest]的值 // 断言:a[0] ≤a[1] ≤ … ≤ a[first],且它们是原数组项中的最小项。 // 其余的数据项从a[first+1]开始 selectionSort(a, first+1, last) } java实现时,因为参数包括first和last,所以方法头和之前迭代不同 public static } // end selectionSort 8.2.3 选择排序的效率 迭代方法selectionSort中,for循环执行n-1次,所以它分别调用getIndexOfSmallest和swap方法各n-1次。在n-1次调用getIndexOfSmallest时,last是n-1,而first从0变到n-2.共n(n-1)/2,(比较也是n(n-1)/2次)。因为循环中每个操作都是O(1)的,所以选择排序是O(n2)的。讨论的是不依赖于数组中数据的初始情况,它可以是完全无序的、接近有序的或完全有序的。任何情况下,都是O(n2)的。 注:选择排序的时间效率 选择排序是O(n2)的,不论数组中项的初始次序如何。虽然排序需要O(n2)次比较,但它仅执行O(n)次交换所以选择排序仅有很少的数据移动。 8.3 插入排序 8.3.1 迭代插入排序 对数组的插入排序将数组分隔(partition)(即划分)为两部分。第一部分是有序的,初始时仅含有数组中的第一项。第二部分含有其余的项。算法从未排序部分移走第一项,并将它插入有序部分中合适的有序位置。 对整数数组进行升序排序的插入排序 Algorithm insertionSort(a, first, last) // 迭代地排序数组项a[first]到a[last]。 for (unsorted = first + 1 through last){ nextToInsert = a[unsorted] insertInOrder(nextToInsert, a, first, unsorted - 1) } 有序部分含有一个项a[first],所以算法中的循环从first+1开始并处理待排序部分。然后调用另一个方法(insertInOrder)来执行插入。anEntry是要插入正确位置的值,begin和end是数组的下标。 Algorithm insertInOrder(anEntry, a, begin, end) // 将anEntry插入有序项a[begin]到a[end]中 index = end // 有序部分中最后一项的下标 // 在有序部分为另一个项腾空间,如果需要 while((index >= begin) and (anEntry
a[index+1] = a[index] // 腾空间 index-- } // 断言:a[index+1]空出来了 a[index+1] = anEntry // 插入 8.3.2 递归插入排序 描述:对数组中除最后一个元素外的全部元素进行排序(比排序整个数组更小的问题)则可以将最后元素插入数组其他元素中的合适位置。 Algorithm insertionSort(a, first, last) // 递归地排序数组项a[first]到a[last] if (数组中的项多余一项){ 排序数组项a[first]到a[last-1] 将最后一项a[last]插入数组其余部分的正确有序位置 } Java实现 算法insertInOrder 8.3.3 插入排序的效率 8.3.1的迭代算法insertionSort,对于有n项的数组,first是0且last是n-1。则for循环执行n-1次,所以方法insertInOrder被调用n-1次。在insertInOrder中,begin是0且end是0~n-2。每次调用该方法时,insertInOrder内的循环最多执行end-begin+1次。所以这个循环执行的总次数最多是1+2+…+(n-1)=n(n-1)/2,故插入排序是O(n2)的。执行递归插入排序时,与迭代有相同的操作,故也是O(n2)的。 最优情况下插入排序是O(n)的。insertInOrder内的循环将立即退出。 注:插入排序的时间效率 最优时插入排序是O(n),最坏是O(n2),数组越接近有序,插入排序要做的工作越少。 8.3.4 链式节点链的插入排序 假定方法insertInOrder(nodeToInsert)将一个节点插入链中正确的有序位置。将链划分为两部分,第一部分是有序的,初始时它仅含有第一个节点。第二部分是无序的,初始时它含有链中其余的节点。先让变量unsortedPart指向第二个节点,然后将第一个节点的链接部分置为null。 假定要将排序方法添加到使用链来表示某个集合的类LinkedGroup中,因为排序要求比较集合中的对象,所以它们必须实现了接口Comparable的类,所有类定义的开头如下: 这个类有内层类Node,它对其私有数据域有设置(set)方法和获取(get)方法。下的私有方法将nodeToInsert指向的节点插入firstNode指向的有序链中。 执行插入排序的方法如下: 链的插入排序的效率 n个节点,方法insertInOrder进行的比较次数最多是链中有序部分的节点个数。方法insertionSort共n-1次。第一次这样做时,有序部分含一项,所以进行了一次比较。第二次时, 有序有两项,最多两次比较。最多比较次数 1+2+…+(n-1)=n(n-1)/2,故插入排序是O(n2)的。 8.4 希尔排序 选择、插入排序比较简单且常用,当它们用于大数组时效率不高,希尔排序是插入排序的变体,比O(n2)更快。 在插入排序过程中,数组项只移动到相邻位置。当项与正确的有序位置相距甚远时,必须进行很多次的移动,当数组完全无序时,插入排序要花很多时间。数组基本有序时,效率高。 Donald Shell在1959年设计了改进的插入排序,为希尔排序(Shell sort)。Shell想让项移到比相邻项更远的位置。所以,他对具有等间距下标的项进行排序。 Shell建议,下标间的初始间隔是n/2,且每趟排序中这个值减半直到为1时。所以最后一步知识对整个数组进行普通的插入排序。 8.4.1 算法 希尔排序的核心是修改插入排序,以便其能在有相等间距项的子数组上进行排序。将8.3.1中描述插入排序的两个算法组合并修改,加入下标间距增量space。 希尔排序的方法将调用上面的方法,并提供任何间隔因子的序列。 8.4.2 希尔排序的效率 虽然使用了多次插入排序而不是仅用一次,但对数组最初的排序远比原始数组要小得多,后来的排序是对部分有序的数组进行的,且最后的排序是对几乎全部有序的数组进行的。 因为incrementalInsertionSort方法设计一个循环,而本身又是在嵌套的循环内被调用,所以希尔排序使用了3层嵌套的循环。这样的算法常是O(n3)的,但希尔排序最坏情况是O(n2)的,如果n是2的幂次,则平均情形是O(n1.5)。如果稍微调整间隔,能使希尔排序的效率更高。 一项改进是避免space是偶数值。space为6,有10,9,7.后来space分半,变为7,4,9,17,10.两个数组有公共项,即10,9,7。所以当space是偶数时进行的比较,会在增量是space/2的下一趟排序中重复。当space为偶数时,只需将其加1。这个简单的修改能得到没有公共因子的连续增量。希尔排序的最坏情形则为O(n1.5)。其他的space序列甚至能得到更高的效率,不过还不能证明。 注:希尔排序的时间效率 之前实现的希尔排序有O(n2)的最坏情形。当space为偶数时,将其加1,则最坏情形可以改进为O(n1.5)。 8.5 算法比较 一般地,选择排序是最慢的算法。利用插入排序最优情形的希尔排序是最快的。 最优情形 平均情形 最坏情形 选择排序 O(n2) O(n2) O(n2) 插入排序 O(n) O(n2) O(n2) 希尔排序 O(n) O(n1.5) O(n1.5) 小结 1) 数组的选择排序选择最小的项并将其与第一项交换。忽略新的第一项,排序寻找数组的其余项中的最小项并将其与第二项交换,以此类推 2) 一般地,迭代执行选择排序,虽然简单的递归形式也是可行的 3) 选择排序在所有情形下都是O(n2)的 4) 插入排序将数组划分为两部分,有序的和未排序的。初始时,数组的第一项属于有序部分。排序算法寻找下一个未排序的项,将它与有序部分中的项进行比较。连续进行比较时,每个有序项向数组尾的方向移动一个位置,直到找到未排序项的正确位置。然后排序将项插入通过移动而腾出的正确位置 5) 可以用迭代或递归方式执行插入排序 6) 最坏情形下插入排序是O(n2)的,但最好情形下是O(n)的。数组越有序,插入排序要做的工作越少 7) 可以使用插入排序对链式节点进行排序,对链式节点排序通常是比较困难的一件事 8) 希尔排序是插入排序的修改版,它对数组内具有相等间隔的项组成的子数组进行排序。这个机制能高效地重排数组,数组几乎有序,从而能使用普通插入排序快速完成工作 9) 之前实现的希尔排序最坏情形是O(n2)的,稍加修改,它的最坏情形至少可改进为O(n1.5)。 (九)排序(选择、插入、希尔) 标签:对象 不能 inf length from sele author lsp 子类 原文地址:https://www.cnblogs.com/datamining-bio/p/9678072.html
/**
* Class for sorting an array of Comparable objects from smallest to largest.
* @author Administrator
*
*/
public class SortArray {
/**
* Sorts the first n objects in an array into ascending order.
* @param a: An array of Comparable objects.
* @param n: An integer > 0.
*/
public static
// Finds the index of the smallest value in a portion of an array a.
// Precondition: a length > last >= first >= 0.
// Returns the index of the smallest value among
// a[first], a[first+1],...,a[last].
private static
// Swaps the array entries a[i] and a[j]
private static void swap(Object[] a, int i, int j) {
Object temp = a[i];
a[i] = a[j];
a[j] = temp;
} // end swap
} // end SortArray
selectionSort(a, 0, n -1); // Invoke recursive method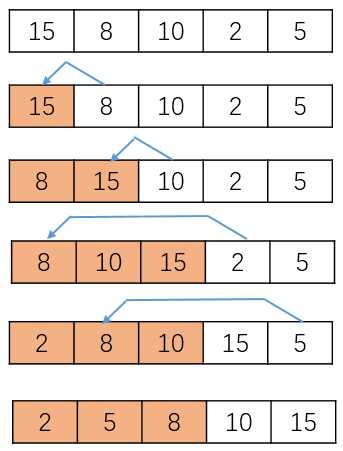
public static
Algorithm insertInOrder(anEntry, a, begin, end)
// 将anEntry插入到有序数组项a[begin]到a[end]中
if (anEntry >= a[end])
a[end + 1] = anEntry
else if (begin end){
a[end + 1] = a[end];
insertInOrder(anEntry, a, begin, end - 1);
}
else{ // begin==end and anEntry
a[end + 1] = a[end];
a[end] = anEntry;
}
public class LinkedGroup
private void insertInOrder(Node nodeToInsert) {
T item = nodeToInsert.getData();
Node currentNode = firstNode;
Node previousNode = null;
// Locate insertion point
while ((currentNode != null) && (item.compareTo(currentNode.getData()) > 0)) {
previousNode = currentNode;
currentNode = currentNode.getNextNode();
} // end while
// Make the insertion
if (previoueNode != null) {
// Insert between previousNode and currentNode
previousNode.setNextNode(nodeToInsert);
nodeToInsert.setNextNode(currentNode);
}
else {
// Insert at beginning
nodeToInsert.setNextNode(firstNode);
firstNode = nodeToInsert;
} // end if
} // end insertInOrder
public void insertionSort() {
// If zero or one item is in the chain, there is nothing to do
if (length > 1) {
assert firstNode != null;
// Break chain into 2 pieces: sorted and unsorted
Node unsortedPart = firstNode.getNextNode();
assert unsortedPart != null;
firstNode.setNextNode(null);
while (unsortedPart != null) {
Node nodeToInsert = unsortedPart;
unsortedPart = unsortedPart.getNextNode();
insertInOrder(nodeToInsert);
} // end while
} // end if
} // end insertionSort
Algorithm incrementalInsertionSort(a, first, last, space)
// 将a[first…last]中等间距的数组项进行升序排序。
// first >= 0 and = first and // 在要排序的项的下标间,space是不同的。
for (unsorted = first + space 到 last以space为增量){
nextToInsert = a[unsorted]
index = unsorted – space
while ((index >= first) and (nextToInsert.compareTo(a[index]) )){
a[index + space] = a[index]
index = index - space
}
a[index+space] = nextToInsert
}
Algorithm shellSort(a, first, last)
// 将数组a[first…last]中的项进行升序排序。
// first >= 0 and = first and
n = 数组的项数
space = n/2
while(space > 0){
for(begin = first through first + space - 1){
incrementalInsertionSort(a, begin, last, space)
}
space = space / 2
}