标签:solution vector -o 距离 push image == memset 排序
题面
传送门:https://www.luogu.org/problemnew/show/P3953
Solution
这是一道神题
首先,我们不妨想一下K=0,即求最短路方案数的部分分。
我们很容易可以想到一个做法,就是魔改迪杰斯特拉做法:
如果一个点可以更新到达其他点的距离,那个点的方案数就是这个点的方案数;如果一个点所更新出来的距离和之前的相等,那个点的方案数加等当前点的方案数。
用式子可以表现为:
f[j]=f[i] (dis[j]>dis[i]+x)
f[j]+=f[i] (dis[j]==dis[i]+x)
(i表示当前点,j表示它更新的点,x为i到j那条路的距离)
那我们怎么保证它的顺序不会出错,即如何保证一个点去更新其他点的方案数的时候,这个点的方案数是正确的呢?
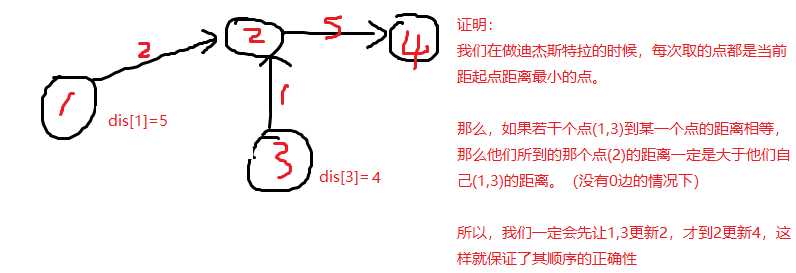
事实上,这种做法就是一种DP。
那么,对于K!=0的情况怎么处理呢?
观察数据,我们会发现K最大只有50。
因此,我们可以考虑在DP上加一维来解决这个K值。
考虑这样设状态:
f[i][j] 表示到达i点,距离为dis[i]+j 的方案数
转移非常好写
f[i][j] = sigema (f[k][dis[i]+j-dis[k]-a]) (k为直接连到i的点,a表示它们之间的边权)
初始化其实我们在30分做法中就已经求好了。
转移顺序是个问题。
我们显然可以在外层枚举j,问题是,有时候,dis[i]+j-dis[k]-a会等于j,如果枚举i的顺序错了,答案肯定会跟着错。
对于dis[i]+j-dis[k]-a==j 的点,肯定是k去更新i,又因为边权没有负值,所以我们就可以按照dis从小到大去去枚举i的值。
以上是没有零边的做法。
对于有零边的情况,我们刚刚的做法就会出问题。如图:
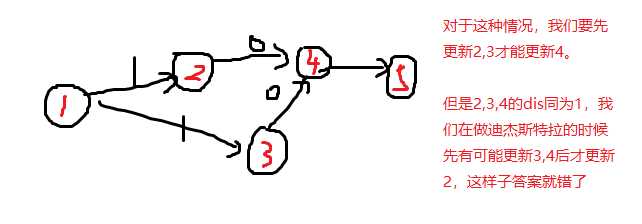
所以说,我们把原图转换一下,只保留0边,对新图做拓扑排序。
如果做完拓扑排序之后,有几个点没有进入过排序中,就说明这个图有零环,就gg了。
我们把拓扑序做完之后再执行原来有的最短路和dp,这样就不会错了。
就酱,我们就嘴巴AC这道题啦o(* ̄▽ ̄*)o 。
事实上,这样做并A不了,因为这题TM卡常(╯°Д°)╯︵┻━┻
然后,你会被卡30分并因此退役(或者是开O2A掉这道题(但是NOIP中并不开O2,所以你还是因此退役了))
Code
//Luogu P3953 逛公园
//Sep,18th,2018
//最短路+拓扑排序+DP+卡常神题
// luogu-judger-enable-o2
#include
#include
#include
#include
#include
#include
using namespace std;
long long read()
{
long long x=0,f=1; char c=getchar();
while(!isdigit(c)){if(c==‘-‘) f=-1;c=getchar();}
while(isdigit(c)){x=x*10+c-‘0‘;c=getchar();}
return x*f;
}
const int N=100000+100;
const int M=50+5;
const int inf=0x3f3f3f3f;
struct DIS
{
int dis,no,zero;
}dis[N];
bool cmp(DIS A,DIS B)
{
if(A.dis==B.dis)
return A.zeroB.zero;
return A.disB.dis;
}
struct road
{
int to,w;
road(int A,int B)
{
to=A,w=B;
}
friend bool operator (road A,road B)
{
if(A.w==B.w)
return dis[A.to].zero > dis[B.to].zero;
return A.w > B.w;
}
};
vector e[N],rev[N];
int n,m,K,poi,T,rd[N],dl2[N],front2,tail2,dis2[N];
long long f[N][M];
priority_queue > dl;
bool vis[N];
void dj()
{
for(int i=1;i)
dis[i].dis=inf,dis[i].no=i;
dis[1].dis=0;
memset(dis2,0x3f,sizeof dis2);
dis2[1]=0;
while(dl.empty()==false) dl.pop();
memset(vis,0,sizeof vis);
dl.push(road(1,0));
f[1][0]=1;
int cnt=0;
while(cnt!=n and dl.empty()==false)
{
road temp=dl.top();
dl.pop();
if(vis[temp.to]==true) continue;
vis[temp.to]=true;
int now=temp.to,dis_now=temp.w;
for(int i=0;iint(e[now].size());i++)
if(dis_now+e[now][i].w dis[e[now][i].to].dis)
{
f[e[now][i].to][0]=f[now][0];
dis[e[now][i].to].dis=dis_now+e[now][i].w;
dis2[e[now][i].to]=dis_now+e[now][i].w;
dl.push(road(e[now][i].to,dis[e[now][i].to].dis));
}
else if(dis_now+e[now][i].w == dis[e[now][i].to].dis)
f[e[now][i].to][0]=(f[e[now][i].to][0]+f[now][0])%poi;
}
}
void GetTP()
{
tail2=front2=0;
memset(vis,0,sizeof vis);
for(int i=1;i)
if(rd[i]==0)
dl2[tail2++]=i;
int cnt=0;
while(tail2>front2)
{
dis[dl2[front2]].zero=++cnt;
vis[dl2[front2]]=true;
for(int i=0;iint(e[dl2[front2]].size());i++)
if(e[dl2[front2]][i].w==0 and vis[e[dl2[front2]][i].to]==false)
{
rd[e[dl2[front2]][i].to]--;
if(rd[e[dl2[front2]][i].to]==0)
dl2[tail2++]=e[dl2[front2]][i].to;
}
front2++;
}
}
int main()
{
T=read();
for(int i=1;i)
e[i].reserve(4),rev[i].reserve(4);
for(;T>0;T--)
{
memset(f,0,sizeof f);
memset(rd,0,sizeof rd);
n=read(),m=read(),K=read(),poi=read();
for(int i=1;i)
e[i].clear(),rev[i].clear();
for(int i=1;i)
{
int a=read(),b=read(),c=read();
e[a].push_back(road(b,c));
rev[b].push_back(road(a,c));
if(c==0)
rd[b]++;
}
GetTP();
bool OK=true;
for(int i=1;i)
if(vis[i]==false)
OK=false;
if(OK==false)
{
printf("-1\n");
continue;
}
dj();
sort(dis+1,dis+1+n,cmp);
for(int j=1;j)
for(int i=1;i)
for(int k=0;kint(rev[dis[i].no].size());k++)
{
int t=dis[i].no,s=rev[t][k].to;
if(dis2[t]!=inf and dis2[s]!=inf and dis2[t]+j-dis2[s]-rev[t][k].w>=0 )
f[t][j]=(f[t][j]+f[s][dis2[t]+j-dis2[s]-rev[t][k].w])%poi;
}
long long ans=0;
for(int i=0;i)
ans=(ans+f[n][i])%poi;
printf("%lld\n",ans);
}
return 0;
}
[Luogu P3953] 逛公园 (最短路+拓扑排序+DP)
标签:solution vector -o 距离 push image == memset 排序
原文地址:https://www.cnblogs.com/GoldenPotato/p/9676610.html

