通过两个位置的经纬度坐标计算距离(C#版本)
转自:https://blog.csdn.net/jasonsong2008/article/details/78423496
经纬坐标系中求点到线段距离的方法
转自C语言版本: https://blog.csdn.net/ufoxiong21/article/details/46487001
依据地图上的经纬度坐标计算某个点到多边形各边的距离
转自JAVA版本 https://blog.csdn.net/james_laughing/article/details/72881056?locationNum=12&fps=1
在一些地图的应用中(如求偏航),常常需要求一个点到一条线程的距离,以判断是否远离航线。然而在经纬度坐标中,并没有类似直角坐标系中的公式来计算。在经纬度中,一般应用最广的公式是求两点距离的方法,如何通过两点之间的距离公式来达到计算出点到线段的方法呢,我们先来看在经纬度中求两点距离的计算方法。
一、经纬度中求两点距离的计算方法
网上有很多介绍该计算方法,此处不再 一一阐述。在北半球中:
C = sin(LatA*Pi/180)*sin(LatB*Pi/180) + cos(LatA*Pi/180)*cos(LatB*Pi/180)*cos((MLonA-MLonB)*Pi/180)
Distance = R*Arccos(C)*Pi/180
注1:其中LonA、LatA、LonB、LatB分别是A、B两个点的经纬度值,其中三角函数的输入和输出都采用弧度值
注2:R(地球半径)和Distance单位是相同,如果是采用6378.137千米作为半径,那么Distance就是千米为单位
C语言代码:
double getDistanceBtwP(double LonA, double LatA,double LonB, double LatB)//根据两点经纬度计算距离,X经度,Y纬度
{
double radLng1 = LatA * M_PI / 180.0;
double radLng2 = LatB * M_PI / 180.0;
double a = radLng1 - radLng2;
double b = (LonA - LonB) * M_PI/ 180.0;
double s = 2 * asin(sqrt(pow(sin(a / 2), 2)+ cos(radLng1) * cos(radLng2) * pow(sin(b / 2), 2))) * 6378.137; //返回单位为公里
return s;
}
二、经纬坐标中求点到线段的距离的方法
在经纬坐标系中,求点C(LonC,LatC)到以点A(LonA,LatA)和点B(LonB,LatB)为端点的线段的距离D。此问题可以分为三种情况:
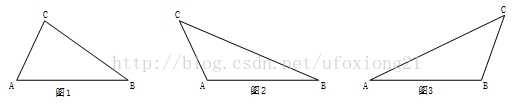
①点C在线段AB的正上方时,则距离D=点C到直线AB的垂直距离,如图1;
②AC与AB形成钝角时,则距离D=线段AC的长度,如图2;
③BC与AB形成钝角时,则距离D=线段BC的长度,如图3;
1、首先如何判断是属于哪种情况
我们可以利用勾股定理逆定理的推广,假如AB、BC、AC的长度分别为a,b,c
①若b*b+c*c
②若a*a+c*c
③若a*a+b*b 2、求图1情况的距离D
我们希望可以通过距离公式即可求出距离D,从而联想到海伦公式。
在海伦公式中,三角形的面积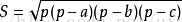 ,其中
,其中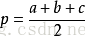 ,则距离D=2S/a;
,则距离D=2S/a;
三、计算方法总结
对于图1情况以及计算出,对于图2和图3的计算均已转换为两个点之间的距离公式,此处不再累赘。因此,在经纬度坐标系中,求点到线段的距离的C语言代码如下:
//点PCx,PCy到线段PAx,PAy,PBx,PBy的距离
double GetNearestDistance(double PAx, double PAy,double PBx, double PBy,double PCx, double PCy)
{
double a,b,c;
a=getDistanceBtwP(PAy,PAx,PBy,PBx);//经纬坐标系中求两点的距离公式
b=getDistanceBtwP(PBy,PBx,PCy,PCx);//经纬坐标系中求两点的距离公式
c=getDistanceBtwP(PAy,PAx,PCy,PCx);//经纬坐标系中求两点的距离公式
if(b*b>=c*c+a*a)return c;
if(c*c>=b*b+a*a)return b;
double l=(a+b+c)/2; //周长的一半
double s=sqrt(l*(l-a)*(l-b)*(l-c)); //海伦公式求面积
return 2*s/a;
}
好了上面是引用的C语言版本的逻辑,我们可以了解了基本的计算逻辑
下面是我经过简单修改过后的C#版本

//地球半径,单位米
private const double EARTH_RADIUS = 6378137;
///
/// 判断是否在误差范围内
///
///
///
///
///
public static bool InLimitDistance(location point, List points, double limitDistance)
{
List distance=new List();
var len = points.Count;
var maxIndex = len - 1;
for (int i = 0; i = c * c + a * a)
{
distance.Add(c);
continue;
}
if (c * c >= b * b + a * a)
{
distance.Add(b);
continue;
}
double l = (a + b + c) / 2; //周长的一半
double s = Math.Sqrt(l * (l - a) * (l - b) * (l - c)); //海伦公式求面积
distance.Add(2 * s / a);
}
if (!distance.Any())
{
return false;
}
var count = distance.Where(s => s 0) return true;
return false;
}
///
/// 计算两点位置的距离,返回两点的距离,单位:米
/// 该公式为GOOGLE提供,误差小于0.2米
///
/// 第一点经度
/// 第一点纬度
/// 第二点经度
/// 第二点纬度
///
private static double GetDistance(location point1, location point2)
{
double radLat1 = Rad(point1.lat);
double radLng1 = Rad(point1.lng);
double radLat2 = Rad(point2.lat);
double radLng2 = Rad(point2.lng);
double a = radLat1 - radLat2;
double b = radLng1 - radLng2;
double result = 2 * Math.Asin(Math.Sqrt(Math.Pow(Math.Sin(a / 2), 2) + Math.Cos(radLat1) * Math.Cos(radLat2) * Math.Pow(Math.Sin(b / 2), 2))) * EARTH_RADIUS;
return result;
}
///
/// 经纬度转化成弧度
///
///
///
private static double Rad(double d)
{
return (double)d * Math.PI / 180d;
}



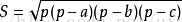 ,其中
,其中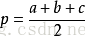 ,则距离D=2S/a;
,则距离D=2S/a;