MIT Hakmem算法的灵魂解析,看不懂算我输
2021-05-28 18:00
标签:例子 情况 ati pre mask line count 32位 opera 首先自己去看这个部分的同学必然是比较好学的了,那么一些前置问题就不解释了,只是解释一些可能大家看起来很突兀的问题,就为啥突然就这样了??为啥就突然这个操作?因为只是解释问题,所以有些公式图片就直接抄其他大佬的了哈! 1.这取模运算怎么就还可以分配律了? 首先有两个概念,取余(rem)和取模(mod)的区别在于前者是让商尽可能趋于0,后者是尽可能让商趋于负无穷. 之前看见有个评论说(3+2)%4=1不等于3%4+2%4=5, 这个例子就举得有问题,3和2都不是4的倍数啊,所以这个例子毫无意义啊. 为啥这里可以分配律呢. 2.这傻逼公式到底啥意思? 其实不知道为啥这么多人写个大N那里几个意思?写个小n不行吗?这里可能有人无法理解为啥成立?为啥要 3.为什么用64作为底? 咱们统计的就是二进制下有多少个1那你必然就要用2的幂作为底了,那为啥不用32呢?因为咱们做的是32位数的,所以最多有可能到32的这个时候就会有特殊情况使得结果为0,所以不采用.那为啥不用128呢?也不是不可以用,用128就得移动6位了,把事情搞复杂了. 4.相信各位对于最开始的代码: 我们该如何理解呢? 其实就是因为我每次用64的幂截留之后的每6位的1个个数最多不过是6,而且两个三bit位的1的个数加起来最多也不过是6,而三bit可以最多表示7所以,相加也不会溢出,所以为了减少位移操作,我们就只移动三位. 拿最低的6位随便举个例子吧,111011,这里就是int t在经过三次位移加mask的操作之后前三位就会变成011010这个时候就变成了2*64^0+3*8*64^0,所以才需要在之后进行 就是这么一回事.加上去了之后高三位依然有旧有的结果,这里很简单直接用000111把高三位的bit过滤掉就完事。懂了吧? 5.最后我们看一下有最终版本的优化吧 MIT Hakmem算法的灵魂解析,看不懂算我输 标签:例子 情况 ati pre mask line count 32位 opera 原文地址:https://www.cnblogs.com/Tonarinototoro/p/14779206.html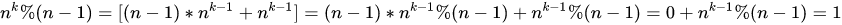
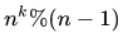 拆成两部分之后呢,前面那部分必然是取模就是0了,后面那部分如果小于n-1那么这个结果很明显(这要是不明显那我也没法子了)也就是对的,那么如果等于n-1呢? 0+0还不是0?大于n-1呢?还不是一样?所以这里这样处理不是因为取模运算可以随便做分配律,而是说这种例子里是没问题的,因为它符合mod运算的原理的.懂?
拆成两部分之后呢,前面那部分必然是取模就是0了,后面那部分如果小于n-1那么这个结果很明显(这要是不明显那我也没法子了)也就是对的,那么如果等于n-1呢? 0+0还不是0?大于n-1呢?还不是一样?所以这里这样处理不是因为取模运算可以随便做分配律,而是说这种例子里是没问题的,因为它符合mod运算的原理的.懂?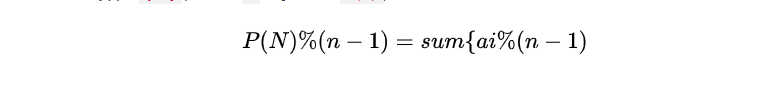
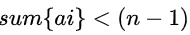 这个大概都知道,因为小于它之后就可以直接=sum嘛.
这个大概都知道,因为小于它之后就可以直接=sum嘛. public static int bitCount(int n){
int t = (n & 010101010101)
+ ((n >>1) & 010101010101)
+ ((n >> 2) & 010101010101)
+ ((n >> 3) & 010101010101)
+ ((n >> 4) & 010101010101)
+ ((n >> 5) & 010101010101);
return t % 63;
}
肯定能够理解0101是用八进制写的哈,别搞错了.
那么对于优化一:public static int bitCountI(int n){
int t = (n & 0b1001001001001001001001001001001)
+ ((n >> 1) & 0b1001001001001001001001001001001)
+ ((n >> 2) & 0b1001001001001001001001001001001);
t = (t + (t >> 3)) & 0b11000111000111000111000111000111;
return t % 63;
}
也可以用八进制代替二进制
0b1001001001001001001001001001001 = 011111111111
0b11000111000111000111000111000111 = 030707070707 t = (t + (t >> 3)) & 0b11000111000111000111000111000111, t>>3就是把之前暂且存在高三个bit位的本该加在低三个bit位的上的统计结果移到了本该到的位置上,然后与原结果相加,记不记得之前说的,相加也不会溢出
这句话?public static int bitCountIII(int n){
int t = n
- ((n>>1) & 0b11011011011011011011011011011011)
- ((n>>2) & 0b1001001001001001001001001001001);
t = (t + (t>>3)) & 0b11000111000111000111000111000111;
}
0b11011011011011011011011011011011 = 033333333333
0b1001001001001001001001001001001 = 011111111111
0b11000111000111000111000111000111 = 030707070707为什么要做这一步操作呢?那当然是为了尽量防止溢出啊(并不是,因为你就算是最高位的64的i次方,统计出来的1的个数也最多只能到000110溢出是不可能的)...那这里是为了啥?
减少一次mask操作吧.int t = n
- ((n>>1) & 0b11011011011011011011011011011011)
- ((n>>2) & 0b1001001001001001001001001001001);思路也很简单,abc如果不表示一个二进制数,那么数的大小是4a+2b+c,我们其实只需要a+b+c,那么其实就等于4a+2b+c-2a-b-a不就是分别mask:000,右移一位再mask011,右移两位mask001?
所以就是以上的结果,后面是一样的步骤.
不知道各位明白了没有.....