最短路径---Dijkstra算法
2021-07-16 04:07
标签:为什么 iostream 最小 ble 顶点 log div tps jsb 是从一个顶点到其余各顶点的最短路径算法,解决的是有向图中最短路径问题。迪杰斯特拉算法主要特点是以起始点为中心向外层层扩展,直到扩展到终点为止。 下面我求下图,从顶点v1到其他各个顶点的最短路径 首先第一步,我们先声明一个dis数组,该数组初始化的值为: 我们的顶点集T的初始化为:T={v1} 既然是求 v1顶点到其余各个顶点的最短路程,那就先找一个离 1 号顶点最近的顶点。通过数组 dis 可知当前离v1顶点最近是 v3顶点。当选择了 2 号顶点后,dis[2](下标从0开始)的值就已经从“估计值”变为了“确定值”,即 v1顶点到 v3顶点的最短路程就是当前 dis[2]值。将V3加入到T中。 OK,既然确定了一个顶点的最短路径,下面我们就要根据这个新入的顶点V3会有出度,发现以v3 为弧尾的有: ,那么我们看看路径:v1–v3–v4的长度是否比v1–v4短,其实这个已经是很明显的了,因为dis[3]代表的就是v1–v4的长度为无穷大,而v1–v3–v4的长度为:10+50=60,所以更新dis[3]的值,得到如下结果: 因此 dis[3]要更新为 60。这个过程有个专业术语叫做“松弛”。即 v1顶点到 v4顶点的路程即 dis[3],通过 这条边松弛成功。这便是 Dijkstra 算法的主要思想:通过“边”来松弛v1顶点到其余各个顶点的路程。 然后,我们又从除dis[2]和dis[0]外的其他值中寻找最小值,发现dis[4]的值最小,通过之前是解释的原理,可以知道v1到v5的最短距离就是dis[4]的值,然后,我们把v5加入到集合T中,然后,考虑v5的出度是否会影响我们的数组dis的值,v5有两条出度:和 ,然后我们发现:v1–v5–v4的长度为:50,而dis[3]的值为60,所以我们要更新dis[3]的值.另外,v1-v5-v6的长度为:90,而dis[5]为100,所以我们需要更新dis[5]的值。更新后的dis数组如下图: 然后,继续从dis中选择未确定的顶点的值中选择一个最小的值,发现dis[3]的值是最小的,所以把v4加入到集合T中,此时集合T={v1,v3,v5,v4},然后,考虑v4的出度是否会影响我们的数组dis的值,v4有一条出度:,然后我们发现:v1–v5–v4–v6的长度为:60,而dis[5]的值为90,所以我们要更新dis[5]的值,更新后的dis数组如下图: 然后,我们使用同样原理,分别确定了v6和v2的最短路径,最后dis的数组的值如下: Aizu - ALDS1_12_B Single Source Shortest Path I 求给定加权图G =(V,E)的单源最短路径的成本 请以G的顶点0为起点,输出0到各顶点v的最短路径上各边权值的总和 输入:第一行输入G的顶点个数n。接下来n行按如下格式输入各顶点u的邻接表 u k v1 c1 v2 c2 v3 c3 ...... G各顶点编号分别为0至n-1。u代表顶点编号,k代表u的出度,vi(i=1,2,3...k)代表与u相邻的顶点编号v及u到v的有向边的权值c 按顺序输出各顶点编号v到0的最短距离 最短路径---Dijkstra算法 标签:为什么 iostream 最小 ble 顶点 log div tps jsb 原文地址:https://www.cnblogs.com/20172674xi/p/9534950.html迪杰斯特拉算法 Dijkstra算法
Dijkstra算法示例演示(摘自Ouyang_Lianjun博客)
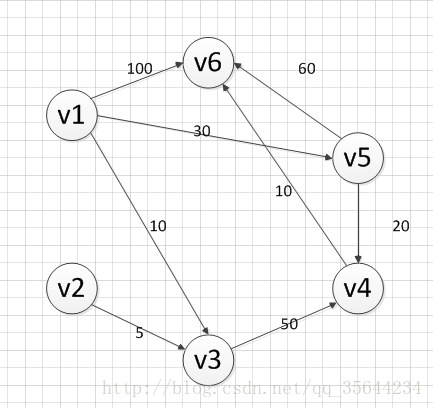

为什么呢?因为目前离 v1顶点最近的是 v3顶点,并且这个图所有的边都是正数,那么肯定不可能通过第三个顶点中转,使得 v1顶点到 v3顶点的路程进一步缩短了。因为 v1顶点到其它顶点的路程肯定没有 v1到 v3顶点短.



例题:
例题链接:https://vjudge.net/problem/Aizu-ALDS1_12_B
题目意思:
AC代码:
#include
下一篇:python调用文件路径