PHP实现排序堆排序(Heap Sort)算法
2018-09-07 11:58
算法引进:
在这里我直接引用《大话数据结构》里面的开头:
在前面讲到简单选择排序 ,它在待排序的 n 个记录中选择一个最小的记录需要比较 n - 1 次,本来这也可以理解,查找第一个数据需要比较这么多次是正常的,否则如何知道他是最小的记录。
可惜的是,这样的操作并没有把每一趟的比较结果保存下来,在后一趟的比较重,有许多比较在前一趟已经做过了,但由于前一趟排序时未保存这些比较结果,所以后一趟排序时又重复执行了这些比较操作,因而记录的比较次数较多。
如果可以做到每次在选择到最小记录的同时,并根据比较结果对其他记录做出相应的调整,那样排序的总体效率就会非常高了。而堆排序,就是对简单选择排序进行的一种改进,这种改进的效果是非常明显的。
基本思想:
在介绍堆排序之前,我们先来介绍一下堆:
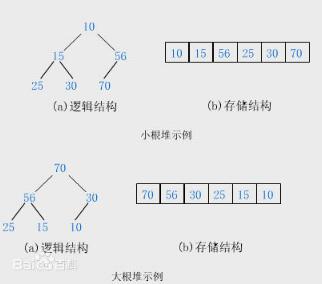
《大话数据结构》里的定义:堆 是具有下列性质的完全二叉树:每个节点的值都大于或等于其左右孩子节点的值,成为大顶堆(大根堆);或者每个节点的值都小于或等于其左右节点的值,成为小顶堆(小根堆)。
当时我在看到这里的时候也对有“堆是否是完全二叉树”有过疑问,网上也有说不是完全二叉树的,但是无论堆是不是完全二叉树,尚且保留意见。我们只要知道,在这里我们采用完全二叉树形式的大根堆(小跟堆),主要是为了方便存储和计算(后面我们会看到带来的便利)。
堆排序算法:
堆排序就是利用堆(假设利用大根堆)进行排序的方法,它的基本思想是:将待排序的序列构造成一个大根堆。此时,整个序列的最大值就是堆顶的根节点。将它移走(其实就是将其与堆数组的末尾元素交换,此时末尾元素就是最大值),然后将剩余的 n - 1 个序列重新构造成一个堆,这样就会得到 n 个元素中的次小的值。如此反复执行,便能得到一个有序序列了。
大根堆排序算法的基本操作:
①建堆,建堆是不断调整堆的过程,从 len/2 处开始调整,一直到第一个节点,此处 len 是堆中元素的个数。建堆的过程是线性的过程,从 len/2 到 0 处一直调用调整堆的过程,相当于 o(h1) + o(h2) …+ o(hlen/2) 其中 h 表示节点的深度, len/2 表示节点的个数,这是一个求和的过程,结果是线性的 O(n)。
②调整堆:调整堆在构建堆的过程中会用到,而且在堆排序过程中也会用到。利用的思想是比较节点i和它的孩子节点 left(i) , right(i),选出三者最大(或者最小)者,如果最大(小)值不是节点i而是它的一个孩子节点,那边交互节点i和该节点,然后再调用调整堆过程,这是一个递归的过程。调整堆的过程时间复杂度与堆的深度有关系,是 lgn 的操作,因为是沿着深度方向进行调整的。
③堆排序:堆排序是利用上面的两个过程来进行的。首先是根据元素构建堆。然后将堆的根节点取出(一般是与最后一个节点进行交换),将前面 len-1 个节点继续进行堆调整的过程,然后再将根节点取出,这样一直到所有节点都取出。堆排序过程的时间复杂度是 O(nlgn)。因为建堆的时间复杂度是 O(n)(调用一次);调整堆的时间复杂度是 lgn,调用了 n-1 次,所以堆排序的时间复杂度是 O(nlgn)。
在这个过程中是需要大量的图示才能看的明白的,但是我懒。。。。。。
算法实现:
<?php //堆排序(对简单选择排序的改进) function swap(array &$arr,$a,$b){ $temp = $arr[$a]; $arr[$a] = $arr[$b]; $arr[$b] = $temp; } //调整 $arr[$start]的关键字,使$arr[$start]、$arr[$start+1]、、、$arr[$end]成为一个大根堆(根节点最大的完全二叉树) //注意这里节点 s 的左右孩子是 2*s + 1 和 2*s+2 (数组开始下标为 0 时) function HeapAdjust(array &$arr,$start,$end){ $temp = $arr[$start]; //沿关键字较大的孩子节点向下筛选 //左右孩子计算(我这里数组开始下标识 0) //左孩子2 * $start + 1,右孩子2 * $start + 2 for($j = 2 * $start + 1;$j <= $end;$j = 2 * $j + 1){ if($j != $end && $arr[$j] < $arr[$j + 1]){ $j ++; //转化为右孩子 } if($temp >= $arr[$j]){ break; //已经满足大根堆 } //将根节点设置为子节点的较大值 $arr[$start] = $arr[$j]; //继续往下 $start = $j; } $arr[$start] = $temp; } function HeapSort(array &$arr){ $count = count($arr); //先将数组构造成大根堆(由于是完全二叉树,所以这里用floor($count/2)-1,下标小于或等于这数的节点都是有孩子的节点) for($i = floor($count / 2) - 1;$i >= 0;$i --){ HeapAdjust($arr,$i,$count); } for($i = $count - 1;$i >= 0;$i --){ //将堆顶元素与最后一个元素交换,获取到最大元素(交换后的最后一个元素),将最大元素放到数组末尾 swap($arr,0,$i); //经过交换,将最后一个元素(最大元素)脱离大根堆,并将未经排序的新树($arr[0...$i-1])重新调整为大根堆 HeapAdjust($arr,0,$i - 1); } } $arr = array(9,1,5,8,3,7,4,6,2); HeapSort($arr); var_dump($arr);
时间复杂度分析:
它的运行时间只要是消耗在初始构建对和在重建堆屎的反复筛选上。
总体上来说,堆排序的时间复杂度是 O(nlogn)。由于堆排序对原始记录的排序状态并不敏感,因此它无论是最好、最差和平均时间复杂度都是 O(nlogn)。这在性能上显然要远远好于冒泡、简单选择、直接插入的 O(n^2) 的时间复杂度了。
堆排序是一种不稳定排序方法。
本篇博客参考自《大话数据结构》,在此仅作记录,方便以后查阅,大神勿喷!
下一篇:php表单习惯用的正则表达式