并查集算法详解
2020-12-13 01:48
标签:报告 最大 人人 输入输出 一点 此刻 数组 false 流程 更好的阅读体验 身为一个数据结构,我们的并查集,它的维护对象是我们的关注点. 传递性,也就是具有传递效应的性质,比如说A传递给B一个性质或者条件,让B同样拥有了这个性质或者条件,那么这就是我们所说的传递性. 连通集合性,和数学概念上的集合定义是差不多的, 比如说A和B同属一个集合,B和C同属一个集合,那么A,B,C都属于同一个集合.这就是我们所谓的连通集合性质. 一般来说数据结构算法,没有所谓的算法步骤,但是却有半确定的模块功能. 数据结构的初始化,通常都是有一个固定的模块,并查集也不例外.对于并查集而言,它的初始化,就是指向的父亲节点. 我们可以想象集合就是一个小圈子,而没一个小圈子都得有一个圈主,那么显然所以人都是围绕着圈主行动的. 同属于一个集合的人们,显然每一个人的指向目标,显然都是这个圈子的圈主. 然而刚开始的时候,显然Acwing的成员们,在没有加入Acwing的时候,基本上都是素不相识的.因此呢,我们所有人肯定是都是属于自己的一个单人小圈子.自己显然就是自己这个小圈子的圈主. 综上所述,我们刚开始,每一个人的指向数组,也就是father数组,肯定都是指向自己. 两个人最远的距离,是沉默,而Acwing这个大家庭,让你我们更加亲近. 海内存知己,天涯若比邻,网络世界的发展,Acwing网站的建立,沟通了身为程序员的你我他. 现在你成为了Acwing的一员,而小A同学也成为了Acwing的一员. 显然通过Acwing这个充满爱的大家庭,使得你和小A同学产生了联系,因此现在你和小A同学同属于一个名为Acwing的集合. 因为你和小A同学,需要建立一种联系,让全世界都知道,你和小A同学都来自富有爱心的网站Acwing大家庭,所以我们就需要用合并操作. 一个人的标签,就是一个人的指向数组,既然你想和小A同学缔结关系的话,那么你和小A同学的指向数组就需要开始变化了. 小A同学是Acwing的金牌元老,他的指示数组就是Acwing,那么身为新成员的你需要修改自己的指向数组,指向小A的同学.说明你和小A同学存在着上下级关系. Acwing是一个充满温情的网站,上下级这种关系显然非常的不友好,那么我们不得不需要斩断这种关系. 你指向着小A同学,小A同学指向着Acwing. 这个大圈子的名字就叫做Acwing,显然小A同学和你同属于Acwing大圈子. 为了让上下级关系消失,我们不得不改变我们的集合指向方式. 我们发现,如果说我们让所有Acwing成员,都指向Acwing这个大家庭的话,那么显然我们的上下级关系消失了,取而代之的则是我们的人人平等,互帮互助的友善关系.也就是我们的Acwing精神主旨之一. Acwing精神不仅仅使得人与人之间更加友好,而且大大提高了我们的工作效率. 比如说如果说N个人,他们之间的关系统统都是上下级关系的话,那么显然我们的工作效率会大大降低. 假如说同学6想要告诉Acwing网站的yxc总裁,一个地方有改进优化的建议,那么他需要不停地往上传递信息,效率是\(O(n)\) 但是如果我们按照人人平等,互帮互助的Acwing精神主旨之一,来进行编排的话,那么显然效率会乘坐火箭,大大提高. 此时我们发现提出一个建议的效率,会大大提高,我们非常完美的处理,让效率成为了\(O(1)\) 原题连接 有 \(n\) 个同学(编号为 \(1\) 到 \(n\) )正在玩一个信息传递的游戏。在游戏里每人都有一个固定的信息传递对象,其中,编号为 \(i\) 的同学的信息传递对象是编号为 \(T_i\) 的同学。 游戏开始时,每人都只知道自己的生日。之后每一轮中,所有人会同时将自己当前所知的生日信息告诉各自的信息传递对象(注意:可能有人可以从若干人那里获取信息, 但是每人只会把信息告诉一个人,即自己的信息传递对象)。当有人从别人口中得知自 己的生日时,游戏结束。请问该游戏一共可以进行几轮? 输入格式: 共\(2\)行。 第\(1\)行包含1个正整数 \(n\) ,表示 \(n\) 个人。 第\(2\)行包含 \(n\) 个用空格隔开的正整数 \(T_1,T_2,\cdots\cdots,T_n\) ,其中第 \(i\) 个整数 \(T_i\) 表示编号为 \(i\) 的同学的信息传递对象是编号为 \(T_i\) 的同学, \(T_i \leq n\) 且 \(T_i \neq i\) 。 输出格式: \(1\)个整数,表示游戏一共可以进行多少轮。 游戏的流程如图所示。当进行完第$ 3$ 轮游戏后, $4 $号玩家会听到 \(2\) 号玩家告诉他自己的生日,所以答案为 \(3\)。当然,第 \(3\) 轮游戏后,$ 2 $号玩家、 \(3\) 号玩家都能从自己的消息来源得知自己的生日,同样符合游戏结束的条件。 对于 \(30\%\)的数据, \(n \le 200\); 对于 \(60\%\)的数据, \(n \le 2500\); 对于$ 100%$的数据, \(n \le 200000\)。 每一轮,每一个人都会将自己手上所有的已知生日信息告诉别人,现在想要求出最少经过多少轮,你会知道你自己的生日信息. 这道题目,直接了断地告诉我们,这道题目具有传递性质.因为我们的信息是传递的. 而且我们发现如果说一个人可以得到属于自己的生日信息的话,那么它肯定处于一个集合(环)之中,不然的话,它肯定无法得到自己的信息. 如下图所示. 这道题目中,每一个就是一个节点,而每一个人手上拥有的信息,我们其实并不在意,因为我们只需要找到那个长度最小的环就好. 这是这道题目样例的解释,我们发现这道题目中,最小的环就是黄绿色部分. 这道题目的核心要点,就是如何找到一个最小环. 这里的算法有很多种,比如说拓扑序,Tarjan,基环树等等,这里当然使用最好写的并查集算法,来Accept这道题目. 这道题目中的联通关系,其实题目中已经给出了,那就是我们的读入数据之中的第二行. 这里可以使用一个小技巧来统计最小环. 我们发现如果说,我们不使用路径优化的并查集算法,那么按照读入顺序,依次连通,会得出如下的图示. 综上所述,我们成功地发现,我们每加入一条连通的关系,如果说在此刻正好发现,我们这个点和目标点,已经有关系了,那么显然我们构成了一个环,那么此时就是最小环 1920年的芝加哥,出现了一群强盗。如果两个强盗遇上了,那么他们要么是朋友,要么是敌人。而且有一点是肯定的,就是: 我朋友的朋友是我的朋友; 我敌人的敌人也是我的朋友。 两个强盗是同一团伙的条件是当且仅当他们是朋友。现在给你一些关于强盗们的信息,问你最多有多少个强盗团伙。 输入的第一行是一个整数N\((2 \le N \le 1000)\),表示强盗的个数(从1编号到N)。 第二行M\((1 \le M \le 5000)\),表示关于强盗的信息条数。 以下M行,每行可能是F p q或是E p q\((1 \le p, q \le N)\),F表示p和q是朋友,E表示p和q是敌人。输入数据保证不会产生信息的矛盾。 输出只有一行,表示最大可能的团伙数。 首先对于一道题目而言,题意是关键,这道题目的题意很简单,就是以上我加粗的黑体字,但是对于一道题目而言,题意往往内含大量条件&性质. 我朋友的朋友也是我的朋友.这句话的含义有两重含义. 我敌人的敌人也是我的朋友,这句话的含义同样有两重含义. 这道题目的分析,其实都在题意理解上面了,总而言之,我们的条件无非就是上面的两点. 以及我们特别解释的两点. 我们发现,如果说对于两人而言的话,假如说我们可以是朋友关系的话,那么我们立即将两人合并到一个集合即可. 然后最大可能的团伙数,其实就是固定确定好的最后团伙数. 并查集算法详解 标签:报告 最大 人人 输入输出 一点 此刻 数组 false 流程 原文地址:https://www.cnblogs.com/gzh-red/p/11011539.html并查集算法详解
算法详解
维护类型
并查集适合维护具有非常强烈的传递性质,或者是连通集合性质.
性质详解
传递性质
连通集合性质
算法步骤
初始化操作
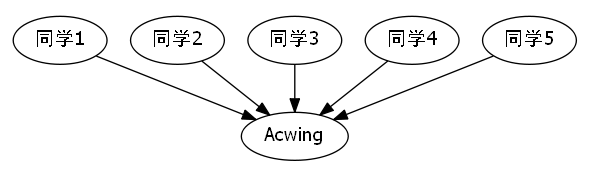
比如说Acwing这个大圈子中,yxc总裁就是我们的红太阳,圈主大人.
合并操作
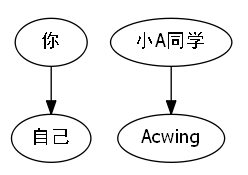
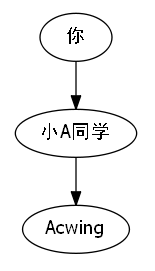
路径压缩

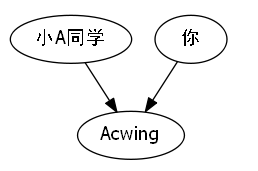
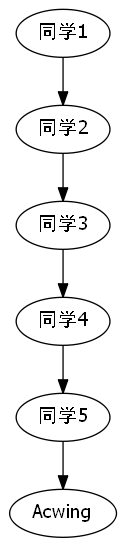
题目选讲
第一题
题目描述
输入输出格式
输入输出样例
输入样例#1:
5
2 4 2 3 1输出样例#1:
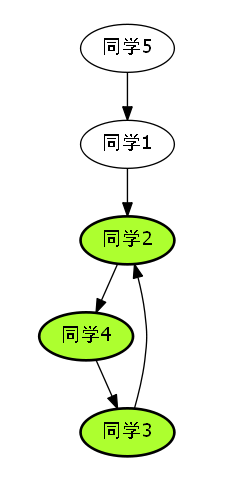
3说明
解题报告
题意理解
性质分析
算法分析
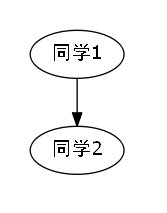
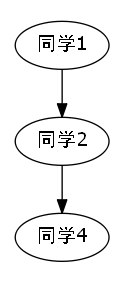
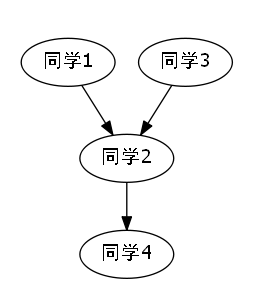
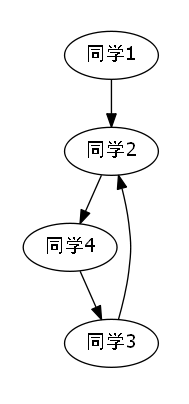
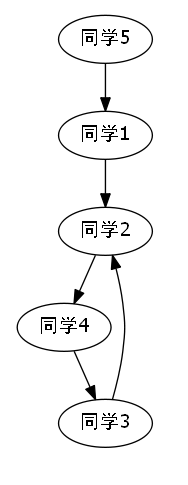
代码解说
#include
第二题
题目描述
输入输出格式
输入格式:
输出格式:
输入输出样例
输入样例#1:
6
4
E 1 4
F 3 5
F 4 6
E 1 2输出样例#1:
3
解题思路
题意理解
比如说师娘显然和y总的桃花们是敌人,但是y总和他的桃花们关系是不确定的.师娘不要打我啊,y总太优秀了.(yxc女粉丝团)
比如说师娘显然追求者不止1个,但是y总和那群追求者的关系,也值得推敲深思.风水轮流转,师娘的微笑
条件分析
思路分析
代码展示
#include
下一篇:javaska