数据结构和算法-最短路径
2020-12-13 01:52
标签:广度优先 最短路径算法 ima heap lock 最小 tar not 时间 针对 Dijkstra(迪杰斯特拉算法): 在 注意: 该算法只适用于 思路: 下表为要从起点到达终点, 数字为花费的时间 上图是按照以上步骤进行填充的 所以最小距离为 利用最小堆实现, 时间复杂度: O(e * logv), e是边的个数 数据结构和算法-最短路径 标签:广度优先 最短路径算法 ima heap lock 最小 tar not 时间 原文地址:https://www.cnblogs.com/zlone/p/11013606.html
无权图可以使用深度优先和广度优先算法, 有权图可以使用最短路径算法有向加权图中查找最短路径有向无环图, 不适用于负权边的情况
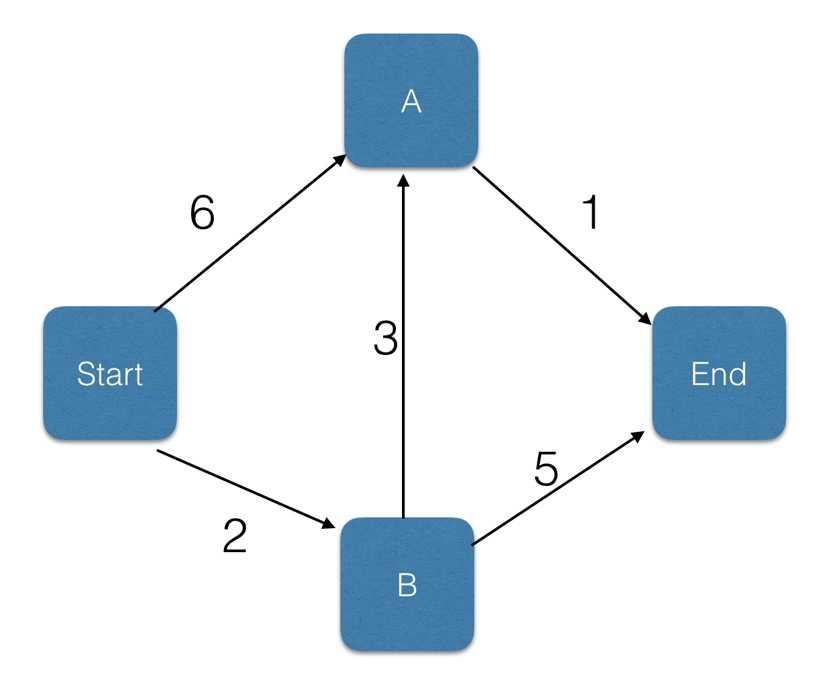
父节点
节点
花费
start
A
6
start
B
2
B
A
5
B
end
7
A
end
6
start的邻居节点A和B, 其中B的花费最少B节点的邻居节点A和end, 更新到A节点的开销A节点进行, 从A到end花费最小, 更新B到end的开销start --> B --> A --> end实现
# -*- coding:utf-8 -*-
'''
Dijkstra算法(最短路径算法)
- 适用于有向有权无环图
- 不适用于负权边的情况
'''
import heapq
class Graph(object):
def __init__(self):
self.graph = {}
def add_edge(self, start: str, end: str, distance: float):
self.graph.setdefault(start, {})
self.graph[start][end] = distance
def dijkstra(start: str, end: str, graph: dict) -> list:
visited = set() # 存储已经处理过的节点
costs = {start: 0}
queue = [(0, start)]
path = {} # 用于复原路径
while queue:
dis, min_node = heapq.heappop(queue)
if min_node == end:
break
if min_node not in visited:
visited.add(min_node)
neighbors = graph[min_node]
for i, j in neighbors.items():
new_dis = dis + j
if (i not in costs) or (new_dis
资料

上一篇:Windows服务器Nginx呗占用端口无法启动的解决
下一篇:关于数组的一些