数据结构与算法之二叉树
2020-12-13 02:10
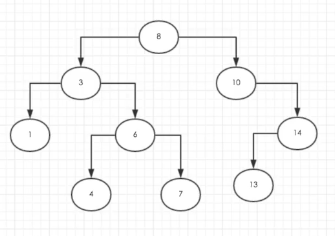
标签:image root min() 方式 hub while 拓展 子节点 get 排序二叉树要求父节点的值大于左节点的值,小于有节点的值。 前序遍历的作用是复制一棵二叉树,它的效率要比重新插入节点来构造要快得多。(8→3→1→6→4→7→10→14→13) 对于排序二叉树来说,中序遍历的结果是升序排序。(1→3→4→6→7→8→10→13→14) 后序遍历 在基于上述的内容我还自己拓展了其他的一些方法(最小最大值,查找节点,删除节点,计算节点数和边数,返回计数对象),并用自己的思路从新将排序二叉树写了一遍,经过测试应该是没有大问题的。 数据结构与算法之二叉树 标签:image root min() 方式 hub while 拓展 子节点 get 原文地址:https://www.cnblogs.com/simpul/p/11027171.html排序二叉树
没有父亲节点的节点称为根节点,没有子节点的节点称为叶子节点,其他都称为中间节点。用JS实现一个排序二叉树
function BinaryTree(){
this.root = null; //初始化根节点为null
}
BinaryTree.prototype = {
constructor: BinaryTree,
insert(key){
var Node = function(key){ //定义一个节点类
this.key = key;
//左右节点初始化为null
this.right = null;
this.left = null;
}
var newNode = new Node(key); //将传入的数值实例化为一个节点
if(this.root === null){
this.root = newNode;
}else{
this.insertNode(this.root, newNode);
}
},
insertNode(node, newNode){ //根据排序二叉树的规则进行节点的插入
if(node.key {
binaryTree.insert(i);
});
console.log(binaryTree); 遍历方式
BinaryTree.prototype.preOrderTraverse = function(callback){ //回调函数用于处理遍历的节点值
this.preOrderTraverseNode(this.root, callback);
}
BinaryTree.prototype.preOrderTraverseNode = function(node, callback){
if(node !== null){
callback(node.key);
this.preOrderTraverseNode(node.left, callback);
this.preOrderTraverseNode(node.right, callback);
}
}
var callback = function(key){
console.log(key);
}
binaryTree.preOrderTraverse(callback);BinaryTree.prototype.inOrderTraverse = function(callback){ //回调函数用于处理遍历的节点值
this.inOrderTracerseNode(this.root, callback);
}
BinaryTree.prototype.inOrderTraverseNode = function(node, callback){
if(node !== null){
this.inOrderTraverseNode(node.left, callback);
callback(node.key);
this.inOrderTraverseNode(node.right, callback);
}
}
var callback = function(key){
console.log(key);
}
binaryTree.inOrderTraverse(callback);BinaryTree.prototype.postOrderTraverse = function(callback){ //回调函数用于处理遍历的节点值
this.postOrderTracerseNode(this.root, callback);
}
BinaryTree.prototype.postOrderTraverseNode = function(node, callback){
if(node !== null){
this.postOrderTraverseNode(node.left, callback);
this.postOrderTraverseNode(node.right, callback);
callback(node.key);
}
}
var callback = function(key){
console.log(key);
}
binaryTree.postOrderTraverse(callback);
总结
//建立二叉树类
function BinaryTree(){
//初始化根节点为null
this.root = null;
}
//建立节点对象(添加到静态方法中)
BinaryTree.Node = function(key){
this.key = key;
this.right = null;
this.left = null;
this.count = 1;
this.show = function(){
return this.key;
}
}
BinaryTree.prototype = {
constructor: BinaryTree,
//插入节点
insert(key){
if(this.isContain(key)){
this.search(key).count += 1;
}else{
var node = new BinaryTree.Node(key);
if(this.root === null){
this.root = node;
}else{
this.insertNode(this.root, node);
}
}
},
insertNode(ref, node){
//根据排序二叉树的规律,左子节点要比父节点小,右子节点要比父节点大
if(ref.key > node.key){
if(ref.left === null){
ref.left = node;
}else{
this.insertNode(ref.left, node);
}
}else{
if(ref.right === null){
ref.right = node;
}else{
this.insertNode(ref.right, node);
}
}
},
//前序遍历
preOrder(cb){ //回调函数用来处理每一个遍历的键值
this.preOrderNode(this.root, cb);
},
preOrderNode(node, cb){
//根据前序遍历的规律,先中间,再左边,最后右边
if(node !== null){
cb(node.key);
this.preOrderNode(node.left, cb);
this.preOrderNode(node.right, cb);
}
},
//中序遍历
inOrder(cb){
this.inOrderNode(this.root, cb);
},
inOrderNode(node, cb){
//根据中序遍历的规律,先左边,再中间,最后右边
if(node !== null){
this.inOrderNode(node.left, cb);
cb(node.key);
this.inOrderNode(node.right, cb);
}
},
//后序遍历
postOrder(cb){
this.postOrderNode(this.root, cb);
},
postOrderNode(node, cb){
//根据后序遍历的规律,先左边,再右边,最后中间
if(node !== null){
this.postOrderNode(node.left, cb);
this.postOrderNode(node.right, cb);
cb(node.key);
}
},
//取得键值最小的节点
getMin(){
//取最左边的子节点
var node = this.root;
while(node.left !== null){
node = node.left;
}
return node;
},
//取得键值最大的节点
getMax(){
//取最右边的子节点
var node = this.root;
while(node.right !== null){
node = node.right;
}
return node;
},
//搜索二叉树中是否包含该键值的节点
isContain(key){
return this.isContainNode(this.root, key);
},
isContainNode(node, key){
if(node === null) return false;
if(node.key === key){
return true;
}else if(node.key > key){
return this.isContainNode(node.left, key);
}else{
return this.isContainNode(node.right, key);
}
},
//给定键值,返回对应的节点
search(key){
return this.searchNode(this.root, key);
},
searchNode(node, key){
if(node === null) return null;
if(node.key === key){
return node;
}else if(node.key > key){
return this.searchNode(node.left, key);
}else{
return this.searchNode(node.right, key);
}
},
//给定键值,返回对象,包含父节点和方向
getParent(key){
var node = this.search(key);
return node ? this.getParentNode(this.root, node) : node;
},
getParentNode(node, child){
if(node === null) return null;
if(node.left === child){
return {parent: node, direction: 'left'};
}else if(node.right === child){
return {parent: node, direction: 'right'};
}else if(child.key > node.key){
return this.getParentNode(node.right, child);
}else{
return this.getParentNode(node.left, child);
}
},
//删除给定键值的节点
remove(key){
var node = this.search(key);
if(node !== this.root){
var {parent, direction} = this.getParent(key);
}
if(node){
if(node.right === null && node.left === null){
//要删除的节点是一个叶子节点
parent[direction] = null;
}else if(node.right === null){
//只含有左子节点
parent[direction] = node.left;
}else if(node.left === null){
//只含有右子节点
parent[direction] = node.right;
}else{
//含有左右两个子节点(选取左子树的最大值或右子树的最小值替换,这里取后者)
var maxNode = node;
while(maxNode.right !== null){
maxNode = maxNode.right;
}
//得到右子树最小值的节点后,先把它自身从二叉树中删除,再把它的键值赋给要删除的节点
this.remove(maxNode.key);
node.key = maxNode.key;
}
}else{
console.log("没有找到相应的节点");
}
},
//返回节点总数
sum(){
var sum = 0;
this.preOrder(()=>{sum++;});
this.sum = sum;
return sum;
},
//返回边的总数
edges(){
this.edges = 0;
this.countEdges(this.root);
return this.edges;
},
countEdges(node){
if(node === null) return false;
if(node.right !== null){
this.edges++;
this.countEdges(node.right);
}
if(node.left !== null){
this.edges++;
this.countEdges(node.left);
}
},
//返回一个对象,属性名是二叉树中节点的键值,属性值是该键值被插入的次数count,用中序法排序
count(){
var obj = {};
var cb = function(key){
obj[key] = this.search(key).count; //这里实际上有性能浪费,排序遍历一次,search又遍历了一次,最好是修改排序遍历中的方法,让它遍历节点而不是键值
}
this.inOrder(cb.bind(this));
return obj;
}
}
上一篇:python 入门知识点总结