算法(递归)---写的很乱

标签：无法   长度   元素   move   时间复杂度   依次   noi   code   number   

前言
本周花了大量的时间再研究算法,这个东西不是一下子就能搞懂的,可能花了大量的时间的看不到见效,也就是得不到一些有效的反馈,这也是我现在比较苦恼的问题,是继续先研究数据结构和算法,还是直接刷leetcode呢?我也不清晰,两眼摸黑,能怎么办呢?学呗,没准一年后就入门了,每天啃一点,没准哪天突然领悟了,后面就会轻松一些

特点

• 找重复
• 找变化
• 找边界

所有的循环都可以改成递归

查找一定区域的范围值
const f2=(a,b)=>{
    if(a>b) return;
    console.log(a);
    return f2(a + 1, b);
};

对数组求和
const f1=(a,b=0)=>{
    if(a.length-1==b) return a[b];
    return a[b]+f1(a,b+1);
};
console.log(f1([1, 2, 3]));

字符串倒序
const s1=(a,b=0)=>{
    if(b == 0 ) return a.charAt(0);
    return a.charAt(b) + s1(a, b - 1);
};
console.log(s1('123456789',2));

const reverse(str)=>{
    if(str.length{
    if(str.length) return true;
    if(str.length==2) return str[0] == str[1];
      if(str[0]==str.slice(-1)){
          return isPalindrome(str.slice(1))
      }
};
console.log(isPalindrome('aka'));

数组扁平化
const flatten = arr => arr.reduce((acc, val) => {
    return acc.concat(Array.isArray(val) ? flatten(val) : val);
}, []);

接受一个对象,这个对象的值是偶数,让其想加

let obj = {
    a: 1,
    b: 2,
    c: {d: 3},
    e: {f: {g: 6}},
    t: {f: {g: {f:10}}},
};
const objSum = obj => {
    let sum = 0;
    for (let key in obj) {
        if (typeof obj[key] == 'object') {
            sum += objSum(obj[key])
        } else if (typeof obj[key] == 'number' && obj[key] % 2 == 0) {
            sum += obj[key];
        }
    }
    return sum
};
console.log(objSum(obj));

const reduceSum=obj=>
    Object.values(obj).
    reduce((acc,val)=>
        typeof val=='object'?
            acc+reduceSum(val):
            acc+val,0);

汉诺塔

讲A柱子上n-1个盘子暂时移到B柱子上

A柱子只剩下最大的盘子,把他移到目标柱子C上

最后再将B柱子上的n-1个盘子移到目标C上

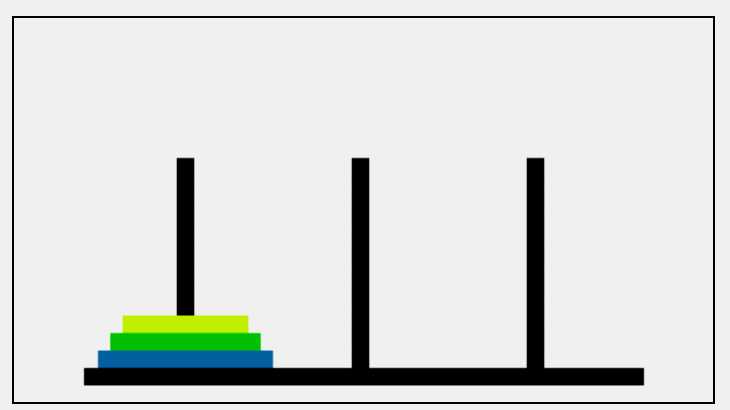
参数
最大编号   初始柱子    辅助的柱子    目标的柱子
const hanoi = (n, a, b, c) => {
    if (n == 1) {
        //a到c
        // move(a, c);
        console.log('Move' + n + ' ' + a + ' ' + c);
    } else {
        // a绕过c放到b
        hanoi(n - 1, a, c, b);
        // move(a, c);
        console.log('Move' + n + ' ' + a + ' ' + c);
        //b绕过a放到c
        hanoi(n - 1, b, a, c);
    }
};
console.log(hanoi(3, 'a', 'b', 'c'));

二分查找递归

左边找(递归)

中间比

右边找(递归)

//在一定范围内L R 求最大值
const getMax=(arr,L,R)=>{
    if(L==R) return arr[L];
    let mid=Math.floor((L+R)/2);
    let maxLeft = getMax(arr, L, mid);
    let maxRight = getMax(arr, mid + 1, R);
    return Math.max(maxLeft, maxRight);
};
let arr = [1, 3, 44, 5, 6, 7, 8];
console.log(getMax(arr, 0, arr.length-1));

希尔排序

　归并排序

举例说明
[9, 3, 6, 4]
[9, 3] | [6, 4]
[9] | [3] [6] | [4]
[3, 9] | [4, 6]
[3, 4, 6, 9]
我们把数组拆分成多个最小的块,可以利用slice方法来实现

//  排序合并
const merge=(left,right)=>{
    let result=[];
    while (left.length > 0 && right.length > 0) {
        if (left[0] {
    if(array.length

基于比较的排序

每一个元素都像一个黑盒子

不需要准备的知道每个元素究竟是什么

只需要能够两两比较他们的大小

插入 比较 冒泡 合并 快速 分块

[1,2,3].sort((a,b)=>a-b)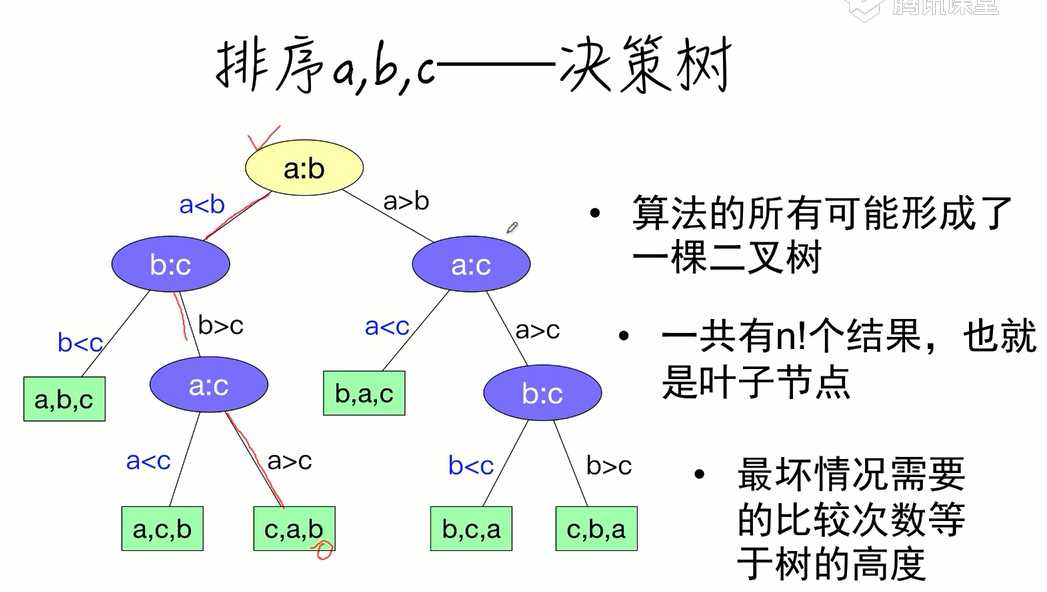

快速排序

类似合并排序--相同点-- 分治策略

先找到一个基准点（一般指数组的中部），然后数组被该基准点分为两部分，依次与该基准点数据比较，如果比它小，放左边；反之，放右边。

const quickSort=arr=>{
    if(arr.length

计数排序

非比较型排序

一般用于范围小于100的排序

时间复杂度为O(n),空间复杂度为数组的数字范围

太变态了,无法理解!!!!

基数排序

每一个元素对应位置上数字的大小进行排序:个位与个位,十位与十位...

看得我头皮发麻,算了,来点轻松的东西

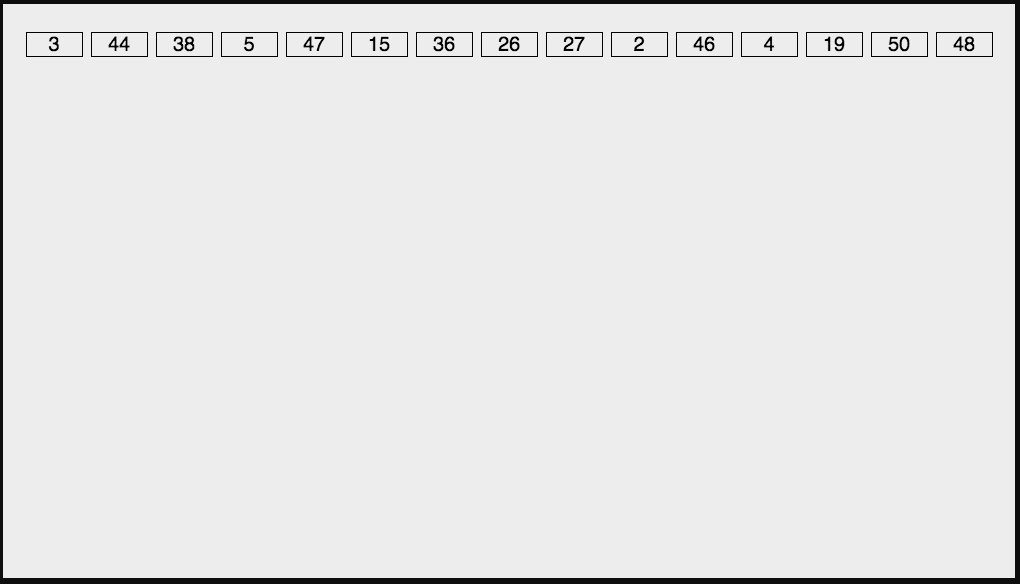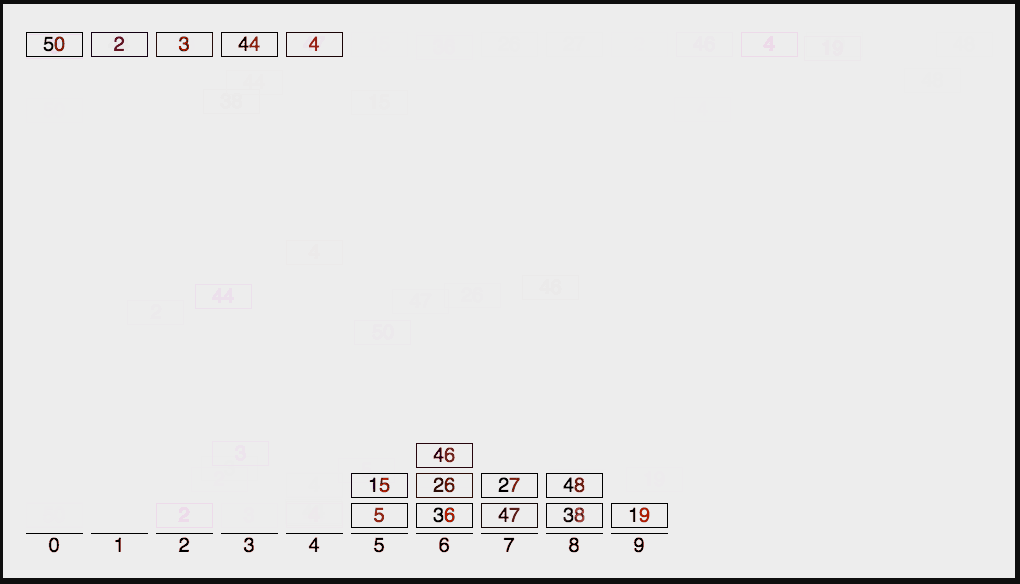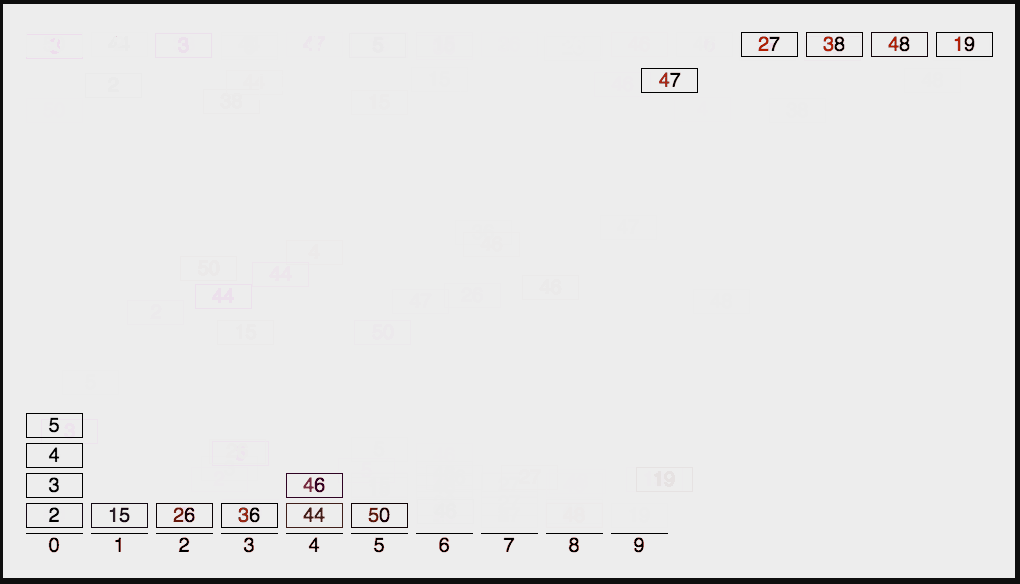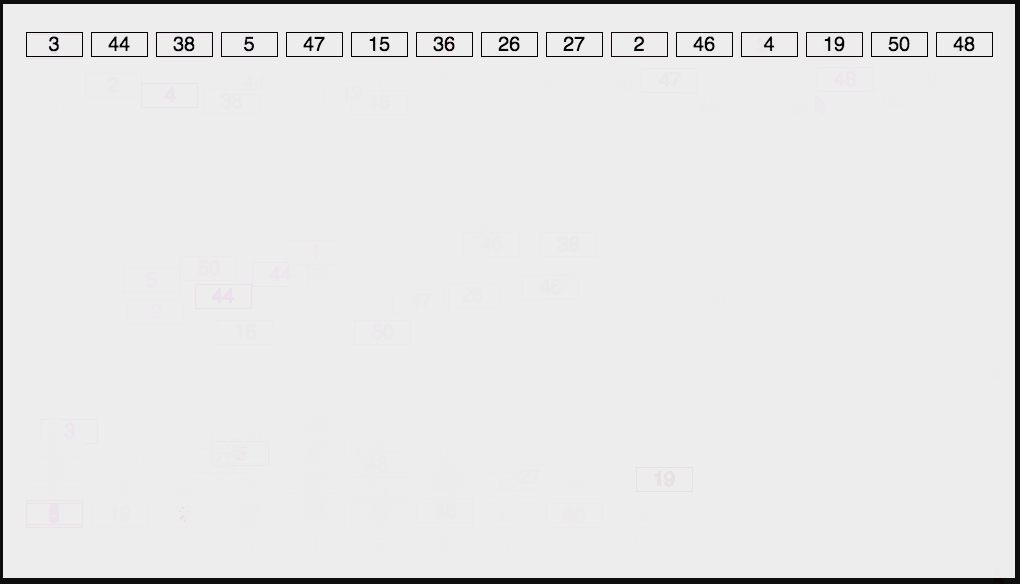
||的妙用

去重(直接保留刚开始的第0项)
const uniq=array=>array.sort((a, b) => a - b)
    .filter((item,index,array)=>!index||item!==array[index-1])

Attribute 和 Property 的区别

"Attribute" 是在html中定义的,而"property" 是在DOM上定义的

说明区别

const input = document.querySelector('input');
console.log(input.getAttribute('value')); // Hello
console.log(input.value); // Hello

console.log(input.getAttribute('value')); // Hello
console.log(input.value); // Hello World!

算法(递归)---写的很乱

标签：无法   长度   元素   move   时间复杂度   依次   noi   code   number   

原文地址：https://www.cnblogs.com/fangdongdemao/p/11073556.html