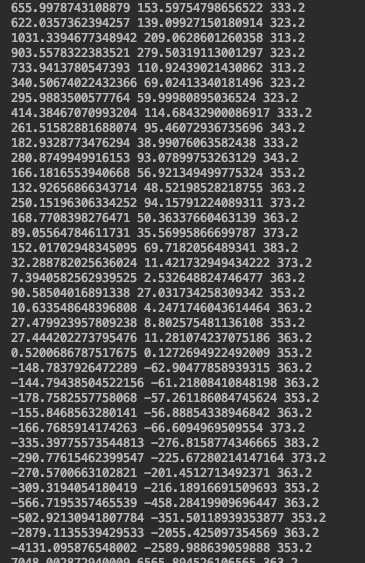
用python计算一条射线到两个平面的交点
2020-12-13 03:23
标签:逻辑 sheet 就是 val ase 计数 cos enumerate 交点 前两天,一个朋友找我(半个程序猿)用python帮他写数学模型,当时的我直接是懵逼的,当听到三维啥的时候,整个人就好了,最终在周末花了3个小时把逻辑理了一遍,给小伙伴一个满意的答复了,话不多说,我来整理一下怎么用python来做数学!!! 首先题目是:建立一个三维坐标,有一个y点和一个x点,假设x点是匀速的,已知第一个x点的坐标,之后的坐标只知道方位角和高低角(相对于y点),相当于确定一个点和一个射线,以之之前的点做球,求球与射线的交点就是下一个点,要得出点的坐标 经分析下来: 初始点z的坐标为343.2 角度a 为方位角 角度b 为高低角 当高低角差值>0的时候 Zn+1 = Zn +10 当高低角差值
当高低角差值=0的时候 Zn+1 = Zn Xn+1 = Rn*1*sin(an+1)*cos(bn+1) Yn+1 = Rn*1*sin(an+1)*sin(bn+1) Zn+1 = Rn*cos(bn+1) 另外有一个excel表里面有方位角和高低角的值 思路就是先求出Z的坐标,再通过去求Rn,从而求出X和Y 表数据 开始码代码 一开始看到excel里几百条数据是懵逼的 一开始居然蠢到手动把数据放到列表里,后面突然想起来了python可以读excel表,于是上网查了下果然可 下面来判断Z的情况 最后执行方法,得到结果。。。 此篇博客主要讲的是用到到excel方法和判断思路,设计数学的一笔带过,如有需要请转载,尊重劳动成果!!! 用python计算一条射线到两个平面的交点 标签:逻辑 sheet 就是 val ase 计数 cos enumerate 交点 原文地址:https://www.cnblogs.com/huizaia/p/11074057.html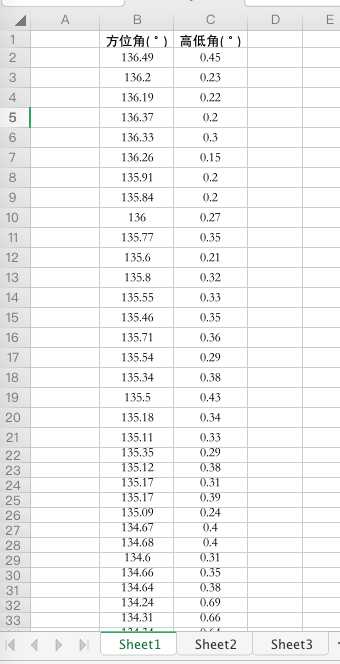
import xlrd
import os
Base_dir = os.path.dirname(__file__)
file_name = ‘data_excel.xlsx‘
file_path = ‘%s/%s‘ % (Base_dir, file_name)
def read_excel():
# 读取excel表里的数据
wb = xlrd.open_workbook(filename=file_path) # 获取整个excel表的内容
sheet1 = wb.sheet_by_index(0) #通过索引获取sheet1这张表
cols = sheet1.col_values(2) # 获取第3列内容(高低角)
high_low_angle_data = cols[1:] 切割把标题切掉,剩下的就是高低角的数据
cols2 = sheet1.col_values(1) 获取第2列的内容(方位角)
azimuth = cols2[1:] 切割把标题切掉,剩下的就是方位角的数据
point_z = 343.2
拓展:
获取表还可以通过name
sheet1 = wb.sheet_by_name(‘sheet1‘)
# 如想要取第二行的数据
hang = sheet1.row_values(1)
#如果要获取136.49
value = sheet1.cell_value(1,1) # 行 列 for key_angle, value_angle in enumerate(high_low_angle_data):
if (value_angle - high_low_angle_data[key_angle+1]) > 0: #当高低角差值大于0时
point_z -= 10
r = point_z/(math.cos(azimuth[key_angle+1]))
x = r*(math.sin(azimuth[key_angle+1])*(math.cos(high_low_angle_data[key_angle+1])))
y = r*(math.sin(azimuth[key_angle+1])*(math.sin(high_low_angle_data[key_angle+1])))
if key_angle == 333:
break
elif (value_angle - high_low_angle_data[key_angle+1]) 0: # 当高低角差值小于0时
point_z += 10
r = point_z / (math.cos(azimuth[key_angle + 1]))
x = r * (math.sin(azimuth[key_angle + 1]) * (math.cos(high_low_angle_data[key_angle + 1])))
y = r * (math.sin(azimuth[key_angle + 1]) * (math.sin(high_low_angle_data[key_angle + 1])))
if key_angle == 333:
break
else:
point_z = point_z #当高低角差值等于0时
r = point_z / (math.cos(azimuth[key_angle + 1]))
x = r * (math.sin(azimuth[key_angle + 1]) * (math.cos(high_low_angle_data[key_angle + 1])))
y = r * (math.sin(azimuth[key_angle + 1]) * (math.sin(high_low_angle_data[key_angle + 1])))
if key_angle == 333:
break
print(x, y, point_z)