python实现二叉树的遍历以及基本操作
2020-12-13 03:40
标签:不能 += while 代码 中序 中序遍历 最短路径 min tor 主要内容: 二叉树遍历(先序、中序、后序、宽度优先遍历)的迭代实现和递归实现; 二叉树的深度,二叉树到叶子节点的所有路径; 首先,先定义二叉树类(python3),代码如下: 内容1:二叉树的遍历 ????????二叉树的遍历分深度优先遍历(DFS)和宽度优先遍历(BFS)。其中深度优先遍历又分为先序遍历,中序遍历,后序遍历。因为二叉树是递归类数据结构,因此大部分关于二叉树的操作都可以通过递归实现。下面将介绍二叉树几种遍历的实现代码以及思路。 1.1 先序遍历: ????????遍历顺序:根节点——左子节点——右子节点(A-B-D-E-C-F)。 递归实现: 迭代实现: 1.2 中序遍历 ????????遍历顺序:左子节点——根节点——右子节点(D-B-E-A-C-F) 递归实现: 迭代实现: 1.3 后序遍历 ????????遍历顺序:左子节点——右子节点——根节点(D-E-B-F-C-A) 递归实现: 迭代实现: 1.4 层次遍历 ????????遍历顺序:一层一层的遍历(A-B-C-D-E-F) 迭代实现: 内容2:基本操作 2.1 二叉树的最大深度 ????????基本思路就是递归,当前树的最大深度等于(1+max(左子树最大深度,右子树最大深度))。代码如下: 2.2 二叉树的最小深度 ????????最小深度是从根节点到最近叶子节点的最短路径上的节点数量。可以通过递归求左右节点的最小深度的较小值,也可以层序遍历找到第一个叶子节点所在的层数。 递归方法: 迭代方法: 2.3 二叉树的所有路径 ????????根节点到叶子节点的所有路径。 python实现二叉树的遍历以及基本操作 标签:不能 += while 代码 中序 中序遍历 最短路径 min tor 原文地址:https://www.cnblogs.com/anzhengyu/p/11083568.html
class TreeNode:
def __init__(self, x):
self.val = x
self.left = None
self.right = None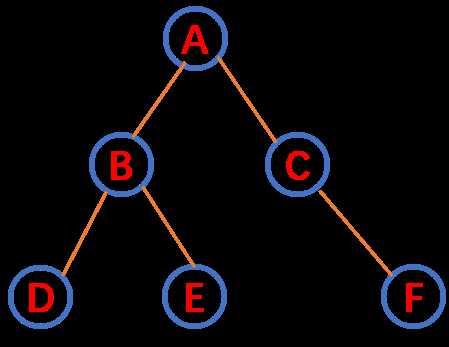
def preorder(root):
if not root:
return
print(root.val)
preorder(root.left)
preorder(root.right) def preorder(root):
stack = [root]
while stack:
s = stack.pop()
if s:
print(s.val)
stack.append(s.right)
stack.append(s.left)def inorder(root):
if not root:
return
inorder(root.left)
print(root.val)
inorder(root.right)def inorder(root):
stack = []
while stack or root:
while root:
stack.append(root)
root = root.left
root = stack.pop()
print(root.val)
root = root.rightdef postorder(root):
if not root:
return
postorder(root.left)
postorder(root.right)
print(root.val)def postorder(root):
stack = []
while stack or root:
while root: # 下行循环,直到找到第一个叶子节点
stack.append(root)
if root.left: # 能左就左,不能左就右
root = root.left
else:
root = root.right
s = stack.pop()
print(s.val)
#如果当前节点是上一节点的左子节点,则遍历右子节点
if stack and s == stack[-1].left:
root = stack[-1].right
else:
root = Nonedef BFS(root):
queue = [root]
while queue:
n = len(queue)
for i in range(n):
q = queue.pop(0)
if q:
print(q.val)
queue.append(q.left if q.left else None)
queue.append(q.right if q.right else None)def maxDepth(root):
if not root:
return 0
return 1+max(maxDepth(root.left),maxDepth(root.right))class Solution:
def minDepth(self, root: TreeNode) -> int:
if not root:
return 0
if not root.left and not root.right:
return 1
if not root.right:
return 1+self.minDepth(root.left)
if not root.left:
return 1+self.minDepth(root.right)
return 1+min(self.minDepth(root.left),self.minDepth(root.right))class Solution:
def minDepth(self, root: TreeNode) -> int:
if not root: return 0
ans,count = [root],1
while ans:
n = len(ans)
for i in range(n):
r = ans.pop(0)
if r:
if not r.left and not r.right:
return count
ans.append(r.left if r.left else [])
ans.append(r.right if r.right else [])
count+=1 def traverse(node):
if not node.left and not node.right:
return [str(node.val)]
left, right = [], []
if node.left:
left = [str(node.val) + x for x in traverse(node.left)]
if node.right:
right = [str(node.val) + x for x in traverse(node.right)]
return left + right