9 Java 堆排序
2020-12-13 03:42
标签:public pre ati sys close click main for static 堆是具有以下性质的完全二叉树,每个结点的值都大于或等于其左右孩子结点的值,称为大顶堆;或者每个结点的值都小于或等于其左右孩子结点的值,称为小顶堆。如下图: 同时,我们对堆中的结点按层进行编号,将这种逻辑结构映射到数组中就是下面这个样子: 该数组从逻辑上讲就是一个堆结构,我们用简单的公式来描述一下堆的定义就是: 大顶堆:arr[i] >= arr[2i+1] && arr[i] >= arr[2i+2] 小顶堆:arr[i]
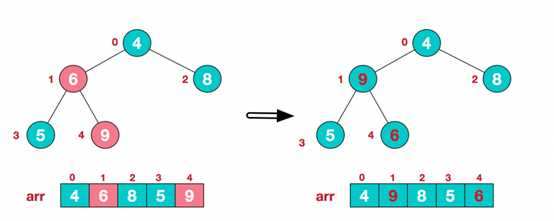
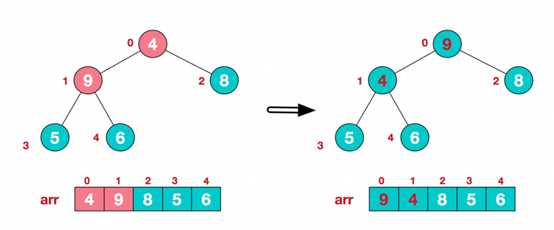
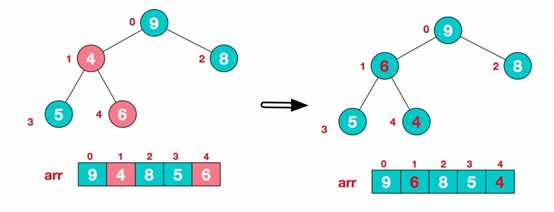
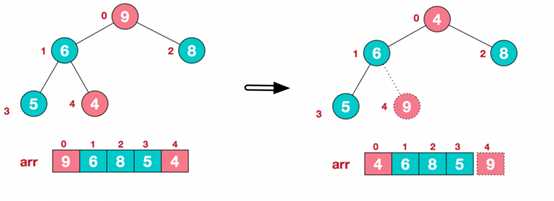
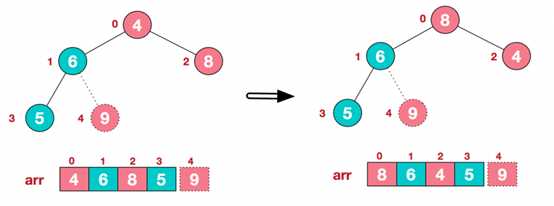
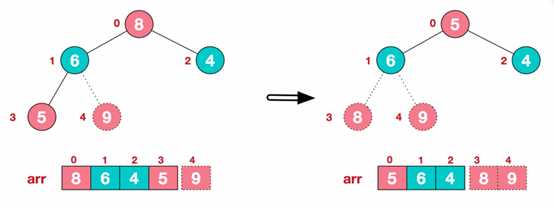
ok,了解了这些定义。接下来,我们来看看堆排序的基本思想及基本步骤: 1、基本思想 将待排序序列构造成一个大顶堆,此时整个序列的最大值就是堆顶的根节点,将其与末尾元素进行交换,此时末尾为最大值。然后将剩余n-1个元素重新构造成一个堆,堆顶继续为n-1个元素的最大值,然后再将其与倒数第二位的元素交换。如此反复执行,便能得到一个有序序列。 2、算法描述 (1) 构造初始堆,将给定无序序列构造成一个大顶堆(一般升序采用大顶堆,降序采用小顶堆)。 假设给定无序序列结构如下: 4 6 8 5 9 此时我们从最后一个非叶子结点开始,顺序从下至上(叶结点自然不用调整,第一个非叶子结点 arr.length/2-1=5/2-1=1,索引1对应的值是6),从左至右,从下至上进行调整。 找到第二个非叶节点4,由于[4,9,8]中9元素最大,4和9交换。 9与4交换之后,该子树[4, 5, 6]为非大顶堆,需要调整为大顶堆,[4, 5 ,6]中6最大,交换4和6。 此时,我们就将一个无需序列构造成了一个大顶堆。每个非叶子节点i 都满足:arr[i] >= arr[2i+1] && arr[i] >= arr[2i+2] (2) 将堆顶元素与末尾元素进行交换,使末尾元素最大。然后继续调整堆,再将堆顶元素与倒数第二元素交换,得到第二大元素。如此反复进行交换、重建、交换。 重新调整剩余n-1个元素的结构,使其继续满足大顶堆排序 再将堆顶元素8与倒数第二元素5进行交换,得到第二大元素8 继续进行调整、交换,如此反复进行,最终使得整个序列有序 再简单总结堆排序的基本思路: 3、代码实现 9 Java 堆排序 标签:public pre ati sys close click main for static 原文地址:https://www.cnblogs.com/Latiny/p/11083466.html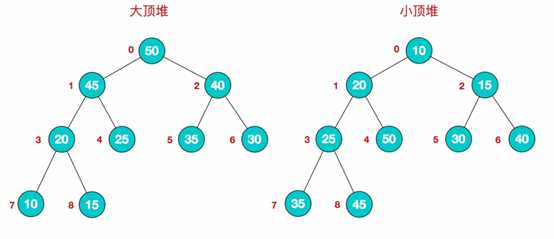

(1) 将无需序列构建成一个堆,根据升序降序需求选择大顶堆或小顶堆;
(2) 将堆顶元素与末尾元素交换,将最大元素"沉"到数组末端;
(3) 重新调整结构,使其满足堆定义,然后继续交换堆顶元素与当前末尾元素,反复执行调整+交换步骤,直到整个序列有序。

public class HeapSort {
public static void main(String[] args) {
Long startTime = System.currentTimeMillis();
//int[] array = new int[]{10, 1, 9, 2, 8, 3, 7, 4, 6, 5};
int[] array = new int[100000];
for (int i = 0; i ) {
array[i] = (int) (Math.random() * 100000);
}
heapSort(array);
Long endTime = System.currentTimeMillis();
System.out.println((endTime - startTime) + " " + array.length);
}
/**
* 堆排序
*
* @param array
*/
public static void heapSort(int[] array) {
// 构建大顶堆
int len = array.length;
for (int i = len / 2 - 1; i >= 0; i--) {
adjustHeap(array, i, len);
}
for (int j = len - 1; j > 0; j--) {
// 将顶上元素与最后元素交换,即最大的元素存放最后
swap(array, 0, j);
// 对剩下的j 个元素继续构建大顶堆
adjustHeap(array, 0, j);
//System.out.println(Arrays.toString(array));
}
}
/**
* 调整大顶堆(仅是调整过程,建立在大顶堆已构建的基础上)
*
* @param array
* @param i
* @param length
*/
public static void adjustHeap(int[] array, int i, int length) {
int temp = array[i];
for (int k = 2 * i + 1; k ) {
if (k + 1 ]) {
k++;
}
if (array[k] > temp) {
array[i] = array[k];
i = k;
} else {
break;
}
}
array[i] = temp;
}
/**
* 交换元素
*
* @param arr
* @param a
* @param b
*/
public static void swap(int[] arr, int a, int b) {
int temp = arr[a];
arr[a] = arr[b];
arr[b] = temp;
}
}