排序算法之归并排序
2020-12-13 04:13
标签:递归函数 开始 列表 针对 image 选择 while else div 一、原理 归并排序(Merge sort)是建立在归并操作上的一种有效的排序算法。将已有序的子序列合并,得到完全有序的序列。如下图: 归并过程: 两个指针的元素比较大小,小的元素就会被放入临时列表中,最后的结果就是: 算法步骤: (1)申请临时空间,使其大小为两个已经排序序列之和,该空间用来存放合并后的序列; (2)设定两个指针,最初位置分别为两个已经排序序列的起始位置,如上图的左侧2和右侧3的位置 (3)比较两个指针所指向的元素,选择相对小的元素放入到合并空间,并移动指针到下一位置; (4)重复步骤 3 直到某一指针达到序列尾; (5)将另一序列剩下的所有元素直接复制到合并序列尾。 二、实现 针对任意个前后有序的序列,将其合并为整个有序的序列,可以实现的代码如下: 上述算法进行的前提序列前后两段已经是有序的,对于任意一个序列如何使用这种算法呢?使用先分解后归并的思想。 实现代码: 排序算法之归并排序 标签:递归函数 开始 列表 针对 image 选择 while else div 原文地址:https://www.cnblogs.com/shenjianping/p/11104497.html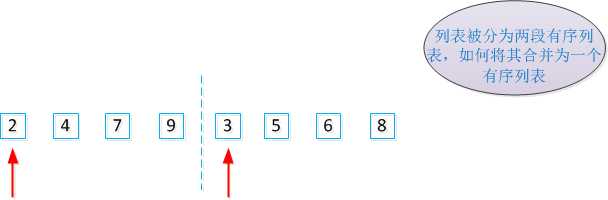
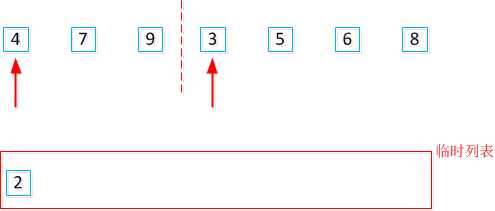
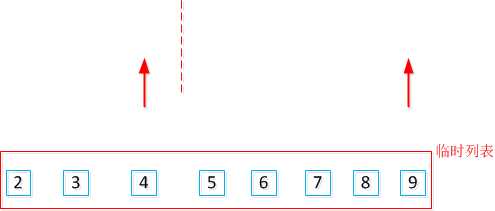
def merge(li,start,mid,last):
"""
:param li: 传入的序列
:param start: 序列第一个位置的索引
:param mid: 序列中间位置的索引
:param last: 序列最后一个元素的索引
:return:
"""
i=start #左边开始指针的位置
j=mid+1 #右边开始指针的位置
temp=[] #申请临时空间
while iand j#当两个指针都没有移动到序列尾部
if li[i]li[j]:
temp.append(li[i])
i+=1
else:
temp.append(li[j])
j+=1
while i#当右边的指针移动到尾部,将左侧的剩下元素全部拷贝到temp
temp.append(li[i])
i+=1
while j#当左边的指针移动到尾部,将右侧的剩下元素全部拷贝到temp
temp.append(li[j])
j+=1
li[start:last+1]=temp #将临时列表中的元素再赋给li列表,节约空间
li=[2,4,7,9,3,5,6,8]
merge(li,0,3,7)
print(li) #[2, 3, 4, 5, 6, 7, 8, 9]
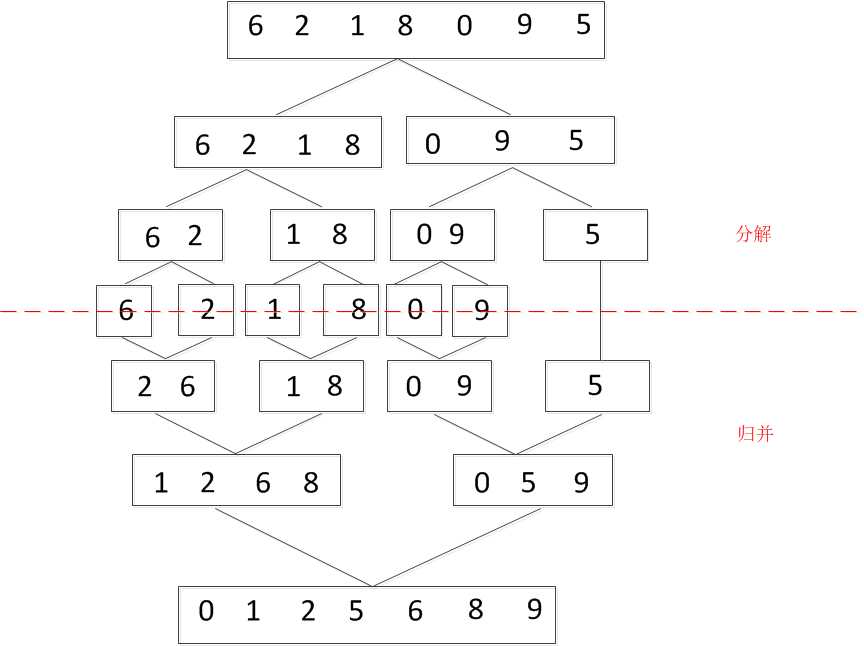
def merge(li,start,mid,last):
"""
:param li: 传入的序列
:param start: 序列第一个位置的索引
:param mid: 序列中间位置的索引
:param last: 序列最后一个元素的索引
:return:
"""
i=start #左边开始指针的位置
j=mid+1 #右边开始指针的位置
temp=[] #申请临时空间
while iand j#当两个指针都没有移动到序列尾部
if li[i]li[j]:
temp.append(li[i])
i+=1
else:
temp.append(li[j])
j+=1
while i#当右边的指针移动到尾部,将左侧的剩下元素全部拷贝到temp
temp.append(li[i])
i+=1
while j#当左边的指针移动到尾部,将右侧的剩下元素全部拷贝到temp
temp.append(li[j])
j+=1
li[start:last+1]=temp #将临时列表中的元素再赋给li列表,节约空间
def mergeSort(li,start,last):
if start