对tarjan——有向图缩点算法的理解
2020-12-13 04:27
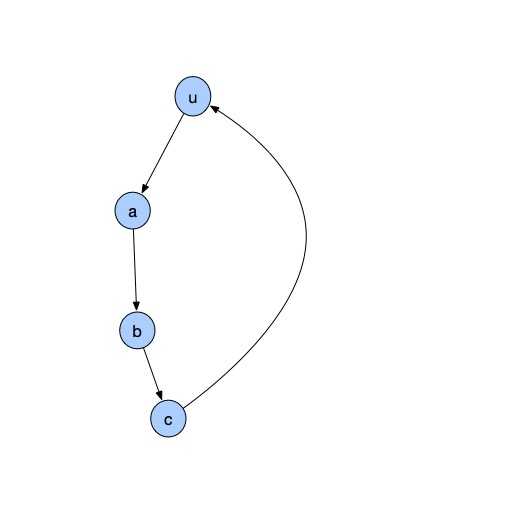
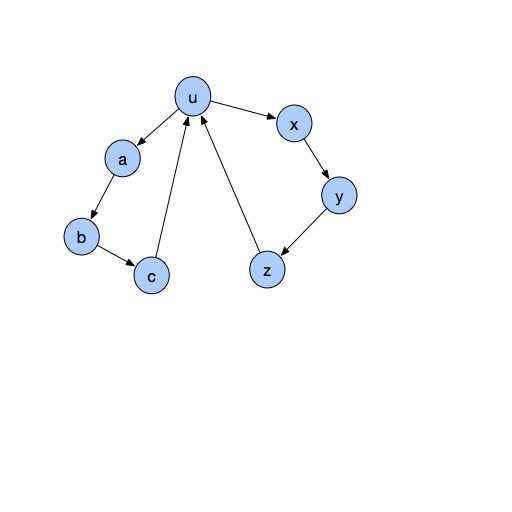
标签:先来 -- 有关 img tarjan info 就是 简单的 结构 开始学tarjan的时候,有关无向图的割点、桥、点双边双缩点都比较容易地理解了,唯独对有向图的缩点操作不甚明了。通过对luoguP2656_采蘑菇一题的解决,大致搞清了tarjan算法的正确性。 首先放出有向图缩点tarjan函数的写法: } while (x != u); 问题主要出在函数的第二部分。遍历完u点的所有边后,第一,为什么将(dfn[u] == low[u])作为构成强连通分量的判定条件?第二,为什么此刻留在栈中的在u之后遍历的点能够构成一个强连通分量? 我们先来考虑一个强连通分量的特征。当有向图中一些点构成的集合是强连通的,当且仅当这部分图满足其中任意两点u、v互通。容易联想到,具有这个特征的典型结构还有有向环;实际上,环是最简单的强连通图,而(感性上)任意一个强连通分量都可以理解成是若干个互通的简单环所构成的。这是一个很重要的想法。笔者认为把复杂的强连通分量简化为环来理解,可以较容易地说明tarjan算法的正确性。 现在我们用两个简单的示意图来说明问题。 如上图,图一表示最简单的环情况,u是当前tarjan函数的起点。我们首先递归地将a、b、c入栈,发现三者的low值都指向了其上的u点,而不是它们自身。tarjan算法对条件(dfn[u] == low[u])的阐述是:满足该条件的u,是某个强连通分量的“根”;换言之,以u为根的搜索子树共同构成一个强连通分量。那么,我们观察这个结论的正确性何在。 1、对于该子树内的两点,若满足i点的时间戳大于j点,则i一定可以通过“前向边”(搜索边)连通至j点,这是显然的。 2、那么,为什么j点又可以通往i点呢?这就是判断条件(dfn[u] == low[u])的由来。显然,j点可以经由最后c点返回u点的那一条边,再从根u沿着前向边到达任意一个i点。 同时,我们可以说明以u为根的原因:如果我们在脑补一条边c-->a,那么a、b、c三点也是强连通的,但是这个连通部分又与u强连通,那么这三点构成的集合便不能成为(极大)强连通分量,a不是“根”。反之,若以u为根的子树不能回溯到还在栈中的更高点而仅能到达u,则这个分量一定是完整的。 图二为子树含两个环的情况,可以认为是更复杂的强连通分量结构。依然,对子树中任意一点v都可以返回到u,然后到达分量中的任意一点,则两个环共同与u构成强连通分量。实际上,任意的强连通结构都符合这个特征,我们总能沿着某条路径回到根,然后到达任意点,而这正是强连通分量的定义。 最后,联想到维护栈的意义:若某些点已经被遍历过而不在栈中,则其参与构成的强连通分量必然已达到最大,不可能与栈中剩余点强连通。典型的例子是横叉边:由当前点可以回到上一个强连通分量中,而那个分量却不存在边能到达当前点,否则这个点早就在那个分量中就被前向边遍历过了。而对于子树中已经弹出的点,一定是各自构成了较小的强连通分量:因为一定存在某个子节点v,使得(dfn[v] == low[v]),即其子树不能回溯到更广的分量范围中。 可能写得有些啰嗦,不太好明白(只有我自己知道我在说什么),所以欢迎有问题或者其他想法的同学在评论区交流。 对tarjan——有向图缩点算法的理解 标签:先来 -- 有关 img tarjan info 就是 简单的 结构 原文地址:https://www.cnblogs.com/TY02/p/11110656.html