编译原理实战入门:用 JavaScript 写一个简单的四则运算编译器(二)语法分析
2020-12-13 04:28
标签:javascrip ref put 算法 需要 执行 new 运算符优先级 一个 以下规则从左往右看,表示左边的表达式还能继续往下细分成右边的表达式,一直细分到不可再分为止。 PS: 对输入的文本按照语法规则进行分析并确定其语法结构的一种过程,称为语法分析。 一般语法分析的输出为抽象语法树(AST)或语法分析树(parse tree)。但由于四则运算比较简单,所以这里采取的方案是即时地进行代码生成和错误报告,这样就不需要在内存中保存整个程序结构。 先来看看怎么分析一个四则运算表达式 首先匹配的是 如下图所示: 这里可能会有人有疑问,为什么一个表达式搞得这么复杂, 有很多算法可用来构建语法分析树,这里只讲两种算法。 递归下降分析法,也称为自顶向下分析法。按照语法规则一步步递归地分析 token 流,如果遇到非终结符,则继续往下分析,直到终结符为止。 递归下降分析法是简单高效的算法,LL(0)在此基础上多了一个步骤,当第一个 token 不足以确定元素类型时,对下一个字元采取“提前查看”,有可能会解决这种不确定性。 以上是对这两种算法的简介,具体实现请看下方的代码实现。 我们通常用的四则运算表达式是中缀表达式,但是对于计算机来说中缀表达式不便于计算。所以在代码生成阶段,要将中缀表达式转换为后缀表达式。 后缀表达式 后缀表达式,又称逆波兰式,指的是不包含括号,运算符放在两个运算对象的后面,所有的计算按运算符出现的顺序,严格从左向右进行(不再考虑运算符的优先规则)。 示例: 中缀表达式: 编译原理的理论知识像天书,经常让人看得云里雾里,但真正动手做起来,你会发现,其实还挺简单的。 如果上面的理论知识看不太懂,没关系,先看代码,再和理论知识结合起来看。 注意:这里需要引入上一篇文章词法分析的代码。 完整源码 编译原理实战入门:用 JavaScript 写一个简单的四则运算编译器(二)语法分析 标签:javascrip ref put 算法 需要 执行 new 运算符优先级 一个 原文地址:https://www.cnblogs.com/woai3c/p/11110519.html四则运算的语法规则(语法规则是分层的)
+ - * /
addExpression 对应 + - 表达式,mulExpression 对应 * / 表达式。语法分析
1 + 2 * 3。expression,由于目前 expression 往下分只有一种可能,即 addExpression,所以分解为 addExpression。
依次类推,接下来的顺序为 mulExpression、term、1(integerConstant)、+(op)、mulExpression、term、2(integerConstant)、*(op)、mulExpression、term、3(integerConstant)。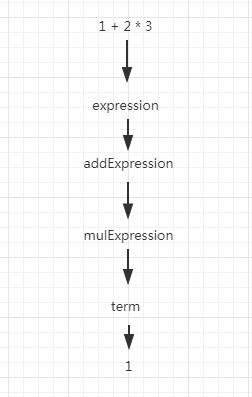
expression 下面有 addExpression,addExpression 下面还有 mulExpression。
其实这里是为了考虑运算符优先级而设的,mulExpr 比 addExpr 表达式运算级要高。1 + 2 * 3
compileExpression
???|?compileAddExpr
???|??|?compileMultExpr
???|??|??|?compileTerm
???|??|??|??|_?matches integerConstant push 1
?|??|??|_
? ?|??|?matches '+'
???|??|?compileMultExpr
???|??|??|?compileTerm
???|??|??|??|_?matches integerConstant push 2
???|??|??|?matches '*'
???|??|??|?compileTerm
??|??|??|??|_?matches integerConstant push 3
???|??|??|_?compileOp('*') *
???|??|_?compileOp('+') +
? |_递归下降分析法
LL(0)分析法
表达式代码生成
5 + 5 转换为后缀表达式:5 5 +,然后再根据后缀表达式生成代码。// 5 + 5 转换为 5 5 + 再生成代码
push 5
push 5
add代码实现
// 汇编代码生成器
function AssemblyWriter() {
this.output = ''
}
AssemblyWriter.prototype = {
writePush(digit) {
this.output += `push ${digit}\r\n`
},
writeOP(op) {
this.output += op + '\r\n'
},
//输出汇编代码
outputStr() {
return this.output
}
}
// 语法分析器
function Parser(tokens, writer) {
this.writer = writer
this.tokens = tokens
// tokens 数组索引
this.i = -1
this.opMap1 = {
'+': 'add',
'-': 'sub',
}
this.opMap2 = {
'/': 'div',
'*': 'mul'
}
this.init()
}
Parser.prototype = {
init() {
this.compileExpression()
},
compileExpression() {
this.compileAddExpr()
},
compileAddExpr() {
this.compileMultExpr()
while (true) {
this.getNextToken()
if (this.opMap1[this.token]) {
let op = this.opMap1[this.token]
this.compileMultExpr()
this.writer.writeOP(op)
} else {
// 没有匹配上相应的操作符 这里为没有匹配上 + -
// 将 token 索引后退一位
this.i--
break
}
}
},
compileMultExpr() {
this.compileTerm()
while (true) {
this.getNextToken()
if (this.opMap2[this.token]) {
let op = this.opMap2[this.token]
this.compileTerm()
this.writer.writeOP(op)
} else {
// 没有匹配上相应的操作符 这里为没有匹配上 * /
// 将 token 索引后退一位
this.i--
break
}
}
},
compileTerm() {
this.getNextToken()
if (this.token == '(') {
this.compileExpression()
this.getNextToken()
if (this.token != ')') {
throw '缺少右括号:)'
}
} else if (/^\d+$/.test(this.token)) {
this.writer.writePush(this.token)
} else {
throw '错误的 token:第 ' + (this.i + 1) + ' 个 token (' + this.token + ')'
}
},
getNextToken() {
this.token = this.tokens[++this.i]
},
getInstructions() {
return this.writer.outputStr()
}
}
const tokens = lexicalAnalysis('100+10*10')
const writer = new AssemblyWriter()
const parser = new Parser(tokens, writer)
const instructions = parser.getInstructions()
console.log(instructions) // 输出生成的汇编代码
/*
push 100
push 10
push 10
mul
add
*/
参考资料:计算机系统要素
上一篇:js数组+运算符
下一篇:【转】java中的反射
文章标题:编译原理实战入门:用 JavaScript 写一个简单的四则运算编译器(二)语法分析
文章链接:http://soscw.com/essay/29516.html