寻找图的强连通分量:tarjan算法简单理解
2020-12-13 05:04
标签:引入 sdn 有向图 深度优先 处理 保存 就是 初始 快速理解 1、简介 2、知识准备 3、快速理解tarjan算法的运行机制 (会被认为是2个环) b.一些不能构成环的点无法被考虑到,而他们本身就是强连通分量 (2不被认为是一个强连通分量) 所以Tarjan算法除了栈还引入了2个数组,分别是: 4、伪代码 6、延伸阅读 寻找图的强连通分量:tarjan算法简单理解 标签:引入 sdn 有向图 深度优先 处理 保存 就是 初始 快速理解 原文地址:https://www.cnblogs.com/Asterism12/p/11129773.html
tarjan是一种使用深度优先遍历(DFS)来寻找有向图强连通分量的一种算法。
栈、有向图、强连通分量、DFS。
提到DFS,能想到的是通过栈来储存沿途的点,可以找到所有的环。环本身就是联通的,所以环对于强连通分量来说环已经很接近最终答案了。要把找环变成找强连通管分量还要考虑:
a.在环外是不是有其他环在这个强连通分量内(极大性)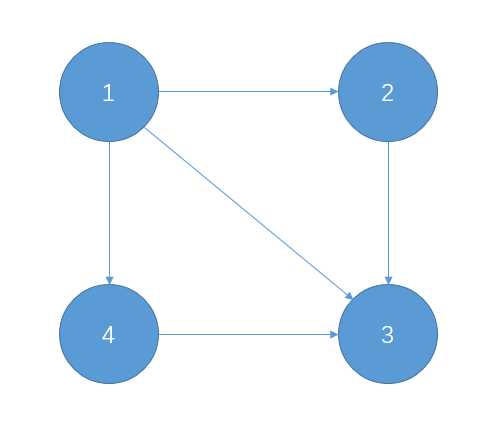
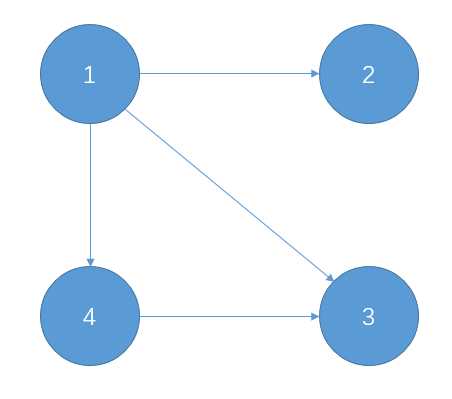
DFN[N]//节点的时间戳,用来标记节点访问的先后顺序(以及是否被访问过)
Low[N]//当前“环”里最先被访问到的节点,相当于当前这个强连通分量里的根
Tarjan的流程是:
DFS,每遇到一个未被访问过的节点就初始化DFN[i]=Low[i]=index++;
如果找到了环,就在遍历中用Low数组向上传递根的时间戳,直到找到一个点他的时间戳和根的时间戳一致,即DFN[i]=Low[i],这就说明这个点就是根。此时,栈内的所有在根后面的点(包括根)就组成一个强连通分量。index=0;
tarjan(u)
{
DFN[u]=low[u]=index++;
u入栈;
for(遍历每条边(u,v))
{
if(v未被访问)
{
tarjan(v);//DFS
low[u]=min(low(u),DFN(v));//将下方的时间戳向上传递
}
else if(v在栈内)
{
low[u]=min(low[u],DFN(v));//找到环,比较当前保存的根的时间戳和v的时间戳,取较早的那个作为根
}
if(DFN(u)==low[u])
{
//回到了根节点,此时栈内从u往后的节点都是该强连通分量的节点
//找到了强连通分量,逐个退栈,输出
}
}
}
5、进一步说明
a.对于问题a,为什么能找到强连通分量内其他的环?
DFS的问题在于,找到了环立即处理而不考虑其他环;Tarjan算法把输出交给根节点处理,在到根节点之前,算法已经遍历的根节点下的所有节点,自然也把所有环放入了栈。
b.对于问题b,为什么考虑到了不能构成环的那些节点?
对于这些节点,DFN(u)==low[u],相当于他们本身就是强连通分量的根节点。
如果您仍然有疑问,可以参考https://blog.csdn.net/qq_34374664/article/details/77488976