知道堆排序吗?
2020-12-13 05:40
标签:最大堆 temp 算法 font com api 其他 堆排 怎么 堆排序介绍 堆排序是指利用堆积树(堆)这种数据结构所设计的一种排序算法,它是选择排序的一种。 可以利用数组的特点快速定位指定索引的元素。堆分为大根堆和小根堆,是完全二叉树。 什么是完全二叉树呢?还有满二叉树又是怎么的一种二叉树呢?还有完满二叉树? 下面用图来说话: 简单来说: 堆排序是将数据看成是完全二叉树、根据完全二叉树的特性来进行排序的一种算法 最大堆要求节点的元素都要不小于其孩子,最小堆要求节点元素都不大于其左右孩子 那么处于最大堆的根节点的元素一定是这个堆中的最大值 完全二叉树有个特性: 堆排序代码实现 : 值得注意的是: 在上面体验堆排序时,我们是左子树和右子数都是已经有 显然,一个普通的数组并不能有这种条件(父>子),因此,我们往往是从数组最后一个元素来进行建堆 接下来不断建堆,然后让数组最后一位与当前堆顶(数组第一位)进行交换即可排序: 知道堆排序吗? 标签:最大堆 temp 算法 font com api 其他 堆排 怎么 原文地址:https://www.cnblogs.com/yslf/p/11145867.html
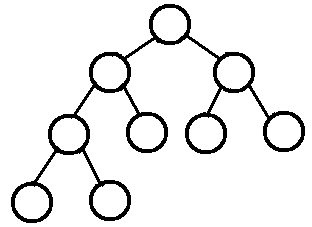
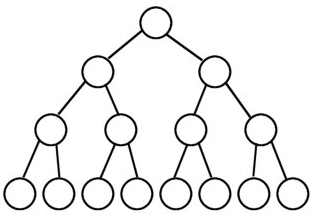
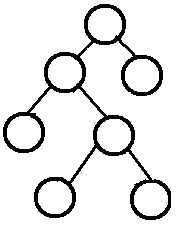
左边子节点位置 = 当前父节点的两倍 + 1,右边子节点位置 = 当前父节点的两倍 + 2 1 /**
2 * 建堆
3 *
4 * @param arrays 看作是完全二叉树
5 * @param currentRootNode 当前父节点位置
6 * @param size 节点总数
7 */
8 public static void heapify(int[] arrays, int currentRootNode, int size) {
9
10 if (currentRootNode size) {
11 //左子树和右字数的位置
12 int left = 2 * currentRootNode + 1;
13 int right = 2 * currentRootNode + 2;
14
15 //把当前父节点位置看成是最大的
16 int max = currentRootNode;
17
18 if (left size) {
19 //如果比当前根元素要大,记录它的位置
20 if (arrays[max] arrays[left]) {
21 max = left;
22 }
23 }
24 if (right size) {
25 //如果比当前根元素要大,记录它的位置
26 if (arrays[max] arrays[right]) {
27 max = right;
28 }
29 }
30 //如果最大的不是根元素位置,那么就交换
31 if (max != currentRootNode) {
32 int temp = arrays[max];
33 arrays[max] = arrays[currentRootNode];
34 arrays[currentRootNode] = temp;
35
36 //继续比较,直到完成一次建堆
37 heapify(arrays, max, size);
38 }
39 }
40 }
父>子这么一个条件的了。 1 /**
2 * 完成一次建堆,最大值在堆的顶部(根节点)
3 */
4 public static void maxHeapify(int[] arrays, int size) {
5
6 // 从数组的尾部开始,直到第一个元素(角标为0)
7 for (int i = size - 1; i >= 0; i--) {
8 heapify(arrays, i, size);
9 }
10
11 }
1 for (int i = 0; i ) {
2
3 //每次建堆就可以排除一个元素了
4 maxHeapify(arrays, arrays.length - i);
5
6 //交换
7 int temp = arrays[0];
8 arrays[0] = arrays[(arrays.length - 1) - i];
9 arrays[(arrays.length - 1) - i] = temp;
10
11 }