kmp算法
2020-12-13 06:03
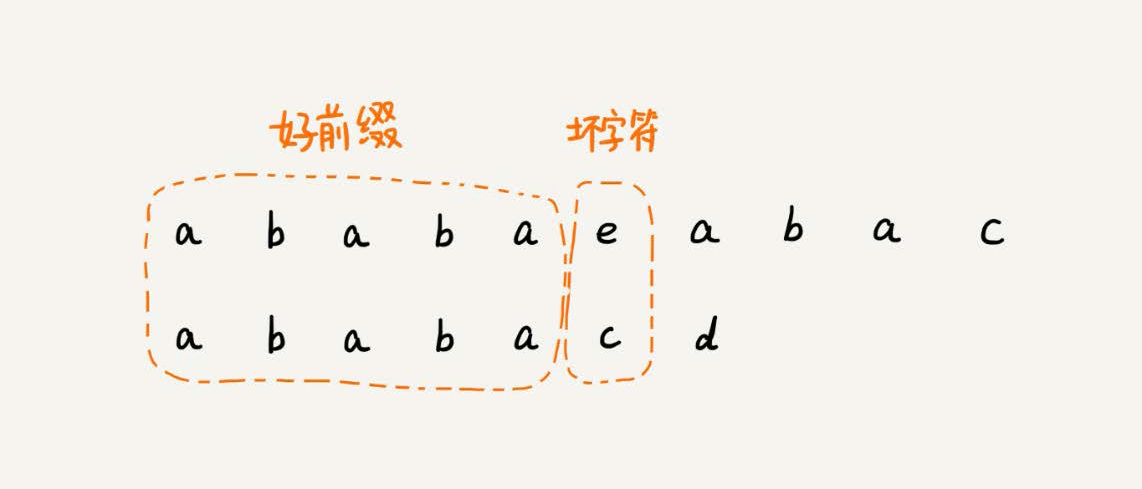
标签:number 复杂 实现 大小 modify 算法 cti 框架 长度 在字符串A中查找字符串B,那字符串A就是主串,字符串B就是模式串 假设主串是a,模式串是b。kmp算法的核心思想就是在模式串与主串匹配的过程中,当遇到不可匹配的字符的时候,找到一些规律,可以将模式串往后多滑动几位,跳过那些肯定不会匹配的情况。 在模式串和主串匹配的过程中,把不能匹配的那个字符仍然叫作坏字符,把已经匹配的那段字符串叫作好前缀。 当遇到坏字符的时候,就要把模式串往后滑动,在滑动的过程中,只要模式串和好前缀有上下重合,前面几个字符的比较,就相当于拿好前缀的后缀子串,跟模式串的前缀子串在比较。那怎么比较呢? KMP算法就是在试图寻找一种规律:在模式串和主串匹配的过程中,当遇到坏字符后,对于已经比对过的好前缀,能否找到一种规律,将模式串一次性滑动很多位? 只需要拿好前缀本身,在它的后缀子串中,查找最长的那个可以跟好前缀的前缀子串匹配的。假设最长的可匹配的那部分前缀子串是{v},长度是k。把模式串一次性往后滑动j-k位,相当于,每次遇到坏字符的时候,就把j更新为k,i不变,然后继续比较。 为了表述起来方便,把好前缀的所有后缀子串中,最长的可匹配前缀子串的那个后缀子串,叫作最长可匹配后缀子串;对应的前缀子串,叫作最长可匹配前缀子串。 求好前缀的最长可匹配前缀和后缀子串,这个问题不涉及主串,只通过模式串本身就能求解。所以,我们事先预处理计算好,在模式串和主串匹配的过程中,直接拿过来用。 我们定义一个next数组用来存储模式串中每个前缀(这些前缀都有可能是好前缀)的最长可匹配前缀子串的结尾字符下标。它有个名字,叫失效函数(failure function)。 数组的下标是每个前缀结尾字符下标,数组的值是这个前缀的最长可以匹配前缀子串的结尾字符下标。 假设next数组已经计算好了,先写出KMP算法的框架代码。KMP算法基本原理







// a, b分别是主串和模式串;n, m分别是主串和模式串的长度。
public static int kmp(char[] a, int n, char[] b, int m) {
int[] next = getNexts(b, m);
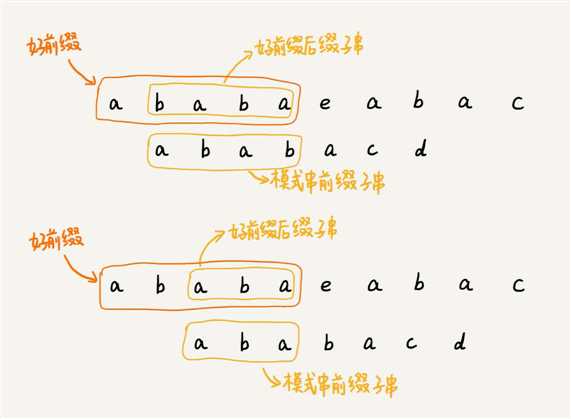
int j = 0;
for (int i = 0; i n; ++i) {
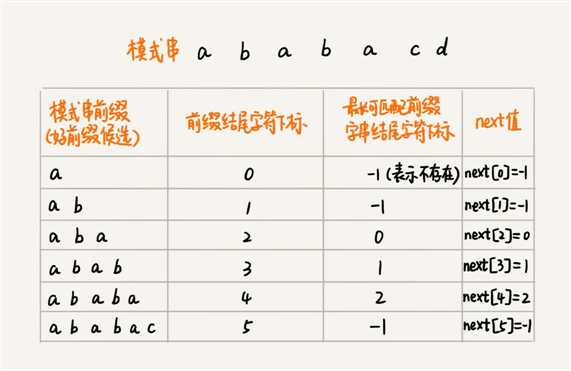
while (j > 0 && a[i] != b[j]) { // 一直找到a[i]和b[j]相等
j = next[j - 1] + 1;
}
if (a[i] == b[j]) {
++j;
}
if (j == m) { // 找到匹配模式串的了
return i - m + 1;
}
}
return -1;
}
失效函数计算方法

我们按照下标从小到大,依次计算next数组的值。当我们要计算next[i]的时候,前面的next[0],next[1],……,next[i-1]应该已经计算出来了。利用已经计算出来的next值,我们可以快速推导出next[i]的值。
如果next[i-1]=k-1,也就表示,子串b[0, k-1]是b[0, i-1]的最长可匹配前缀子串。如果子串b[0, k-1]的下一个字符b[k],与b[0, i-1]的下一个字符b[i]匹配,那子串b[0,k]就是b[0, i]的最长可匹配前缀子串。所以,next[i]等于k。但是,当b[0, k-1]的下一字符b[k]跟b[0, i-1]的下一个字符b[i]不相等时?如何得到next[i]呢?
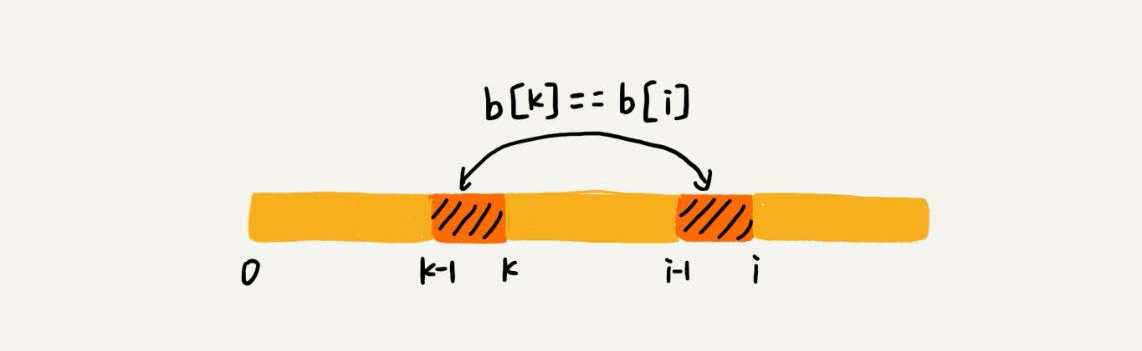

假设b[0, i]的最长可匹配后缀子串是b[r, i]。如果把最后一个字符去掉,那b[r, i-1]肯定是b[0, i-1]的可匹配后缀子串,但不一定是最长可匹配后缀子串。所以,既然b[0, i-1]最长可匹配后缀子串对应的模式串的前缀子串的下一个字符并不等于b[i],那么我们就可以考察b[0, i-1]的次长可匹配后缀子串b[x, i-1]对应的可匹配前缀子串b[0, i-1-x]的下一个字符b[i-x]是否等于b[i]。如果等于,那b[x, i]就是b[0, i]的最长可匹配后缀子串。
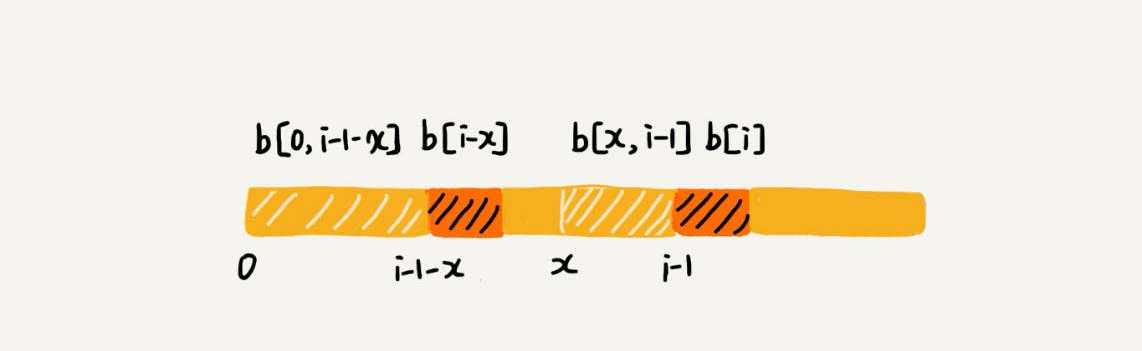

那么如何求次长可匹配后缀子串呢?次长可匹配后缀子串肯定被包含在最长可匹配后缀子串中,而最长可匹配后缀子串又对应最长可匹配前缀子串b[0, y]。于是,查找b[0, i-1]的次长可匹配后缀子串,这个问题就变成,查找b[0, y]的最长匹配后缀子串的问题了。
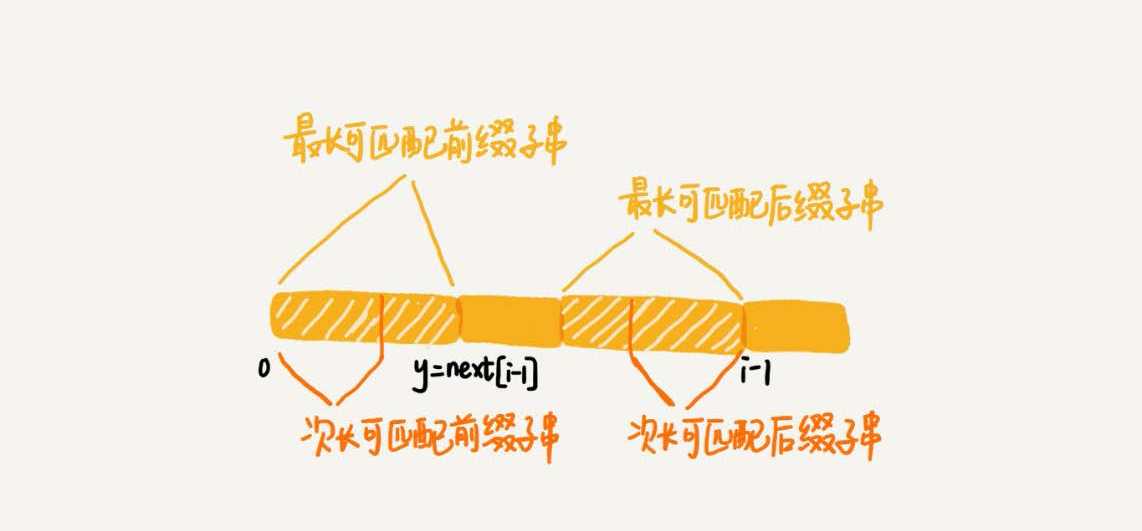

按照这个思路,可以考察完所有的b[0, i-1]的可匹配后缀子串b[y, i-1],直到找到一个可匹配的后缀子串,它对应的前缀子串的下一个字符等于b[i],那这个b[y,i]就是b[0, i]的最长可匹配后缀子串。
结合前面KMP算法的框架代码,和下面求失效函数的代码就是整个KMP算法的代码实现。
// b表示模式串,m表示模式串的长度
private static int[] getNexts(char[] b, int m) {
int[] next = new int[m];
next[0] = -1;
int k = -1;
for (int i = 1; i m; ++i) {
while (k != -1 && b[k + 1] != b[i]) {
k = next[k];
}
if (b[k + 1] == b[i]) {
++k;
}
next[i] = k;
}
return next;
KMP算法复杂度分析
对于空间复杂度,KMP算法只需要一个额外的next数组,数组的大小跟模式串相同。所以空间复杂度是O(m),m表示模式串的长度。
KMP算法的时间复杂度是O(m+n)。
kmp算法
标签:number 复杂 实现 大小 modify 算法 cti 框架 长度
原文地址:https://www.cnblogs.com/mrpeng2333/p/11164597.html