堆排序算法学习小记
2020-12-13 13:58
2.堆的概念
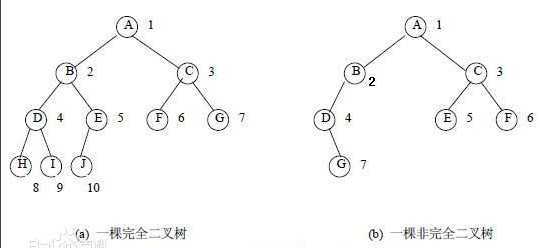
堆(英语:heap)是计算机科学中一类特殊的数据结构的统称。堆通常是一个可以被看做一棵树的数组对象。堆总是满足下列性质:
a.堆中某个节点的值总是不大于或不小于其父节点的值;
b.堆总是一棵完全二叉树。
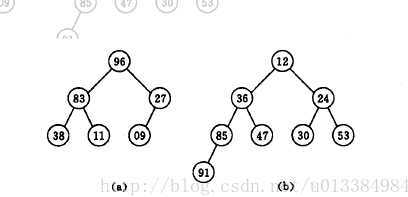
如果某个节点的值总是小于其父节点的值,称为大根堆(a),如果总是大于其父节点的值,称为小根堆(b)。
3.堆排序原理
a.将排序元素构建成堆(升序采用大顶堆,降序采用小顶堆)
b.取出堆顶元素
c.将剩下元素继续构造成堆
重复b c 步骤即可实现堆排序,下面以array=[4,6,8,5,9]数组的升序排序具体说明过程
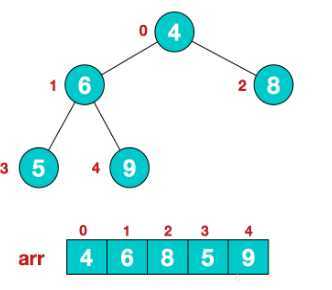
第一步:将数组元素映射成完全二叉树,如上图
第二步:找出完全二叉树中序号最大的非叶子节点(这里比较难理解),这个数+1也是这棵数的非叶子节点数量,下面给出推导过程:
可以分两种情形考虑:
①树的最后一个非叶子节点若只有左孩子
②树的最后一个非叶子节点有左右两个孩子
完全二叉树的性质之一是:如果节点序号为i,在它的左孩子序号为2*i+1,右孩子序号为2*i+2。
对于①左孩子的序号为n-1,则n-1=2*i-1,推出i=n/2-1;
对于②左孩子的序号为n-2,在n-2=2*i-1,推出i=(n-1)/2-1;右孩子的序号为n-1,则n-1=2*i+2,推出i=(n-1)/2-1;
很显然,当完全二叉树最后一个节点是其父节点的左孩子时,树的节点数为偶数;当完全二叉树最后一个节点是其父节点的右孩子时,树的节点数为奇数。
根据java语法的特征,整数除不尽时向下取整,则若n为奇数时(n-1)/2-1=n/2-1。
因此对于②最后一个非叶子节点的序号也是n/2-1。
对于上面给出的完全二叉树结构,根据上面的推导,可以计算出最后一个非叶子节点的 序号 lastNoChildNodeIndex = arr.lenth/2-1=5/2-1=1,即这棵树中序号为0和1的节点均为非叶子节点。
第三步:开始将这棵完全二叉树调整为最大堆,从最后一个非叶子节点开始调整,依次往序号较低的叶子节点进行,上面的树有0,1两个叶子节点,首先调整序号为1的叶子节点
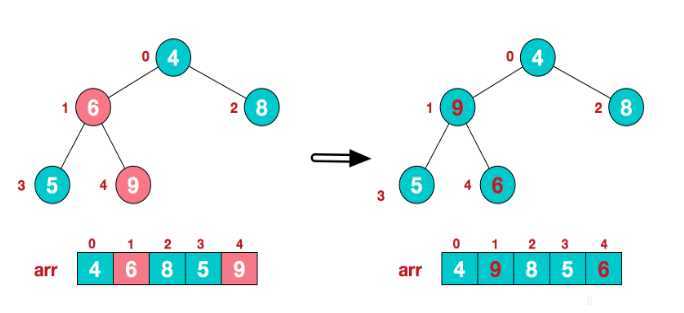
调整思路:序号为1的叶子节点值为6,它的两个子节点分别为5和9,明显,三个值中,最大的值为9,要满足最大堆,9和6交换。按理说,交换值后,需要考虑序号4即6的位置是否满足最大堆要求,但是由于序号4处是叶子节点,所以满足要求。
第四步:调整序号为0的非叶子节点
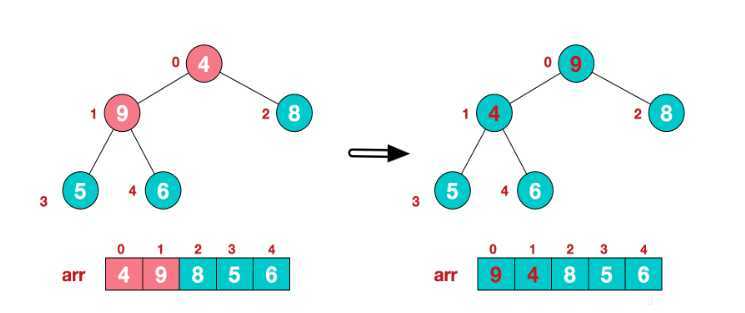
调整思路:
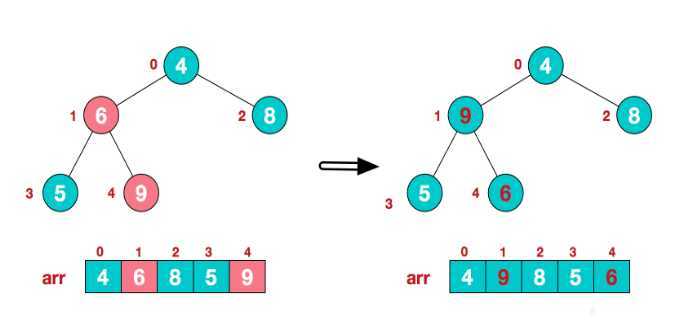
0号节点的值以及两个子节点三个值中,明显9最大,交换4和9的值,此时,被交换过的节点1是非叶子节点,且不满足最大堆要求,下面继续调整节点1使其满足最大堆的要求。
第五步:节点1的三个值中,明显6的值最大,交换6和4的值。
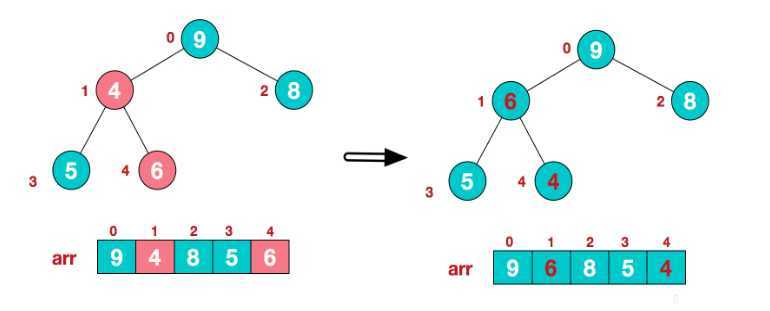
到这里一个最大堆就建立起来了。堆顶元素9即为整个数组的最大值。
第六步:将9和4进行交换,其实就是把9放在树的末尾节点,9后面就不参与排序了。
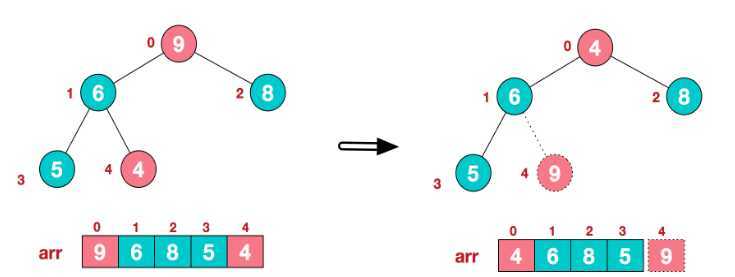
第七步:将剩下的节点用上述方式重新调整为最大堆
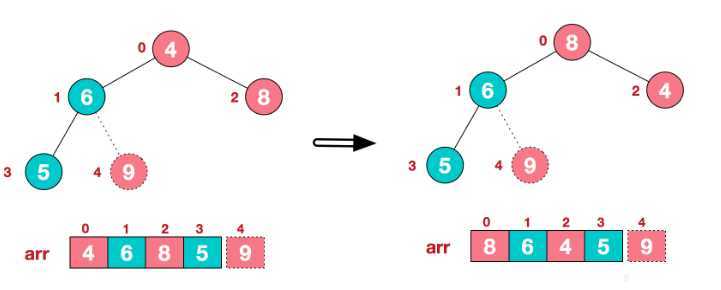
第八步:将堆顶元素8和最后的子节点元素5交换,此时,第二大元素8产生,交换后不再参与排序。
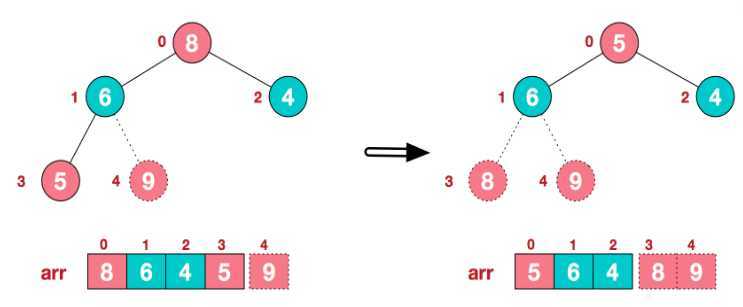
重复上面上述的构建最大堆,将最大元素交换到树节点尾,最后得到的结果如下:
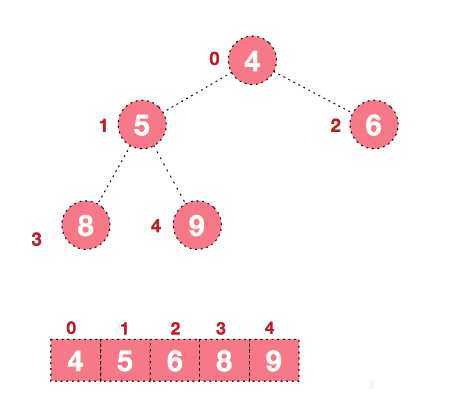
到此,完成了所有排序。
4.堆排序java代码实现
public class heapSorted { public static void main(String[] args) { int[] arr = {4, 6, 8, 5, 9}; for(int i = 0;i){ System.out.println(arr[i]); } arr = sortHeap(arr); for(int i = 0;i){ System.out.println(arr[i]); } } private static int[] sortHeap(int[] arr) { int len = arr.length; //构建最大堆 buildMaxHeap(arr, len); for (int i = len - 1; i > 0; i--) { //堆顶元素(序号为0)和当前堆的最后一个节点(序号i)交换 swap(arr, 0, i); //堆元素总数减一,即将当前树结构最后一个节点排除,不参与下一轮堆结构构建 len--; //重新构建大顶堆 reBuildHeap(arr, 0, len); } return arr; } /** * 构建大顶堆 * @param arr * @param len */ private static void buildMaxHeap(int[] arr, int len) { //(int) Math.floor(len >> 1) = len/2-1 即最大非叶子节点的序号 for (int i = (int) Math.floor(len >> 1); i >= 0; i--) { //从最大非叶子节点开始,依次调整每个非叶子节点,使其满足最大堆要求(比如说最大非叶子节点序号为3,那么一次要调整的非叶子节点为3、2、1、0) //调整完毕,最大堆就构建完成 reBuildHeap(arr, i, len); } } /** * 堆调整 * * @param arr * @param i * @param len */ private static void reBuildHeap(int[] arr, int i, int len) { //1. i为传进来的非子树节点的序号 //2. len为排序数组的长度 //3. left为i节点的左子树节点序号 int left = 2 * i + 1; //4. right为i节点的右子树节点序号 int right = 2 * i + 2; //5. largest为i、left、right三个节点中值最大的节点序号,暂时假定i节点值最大 int largest = i; //6.如果左节点存在并且左节点的值大于最大值节点(目前为i)的值,则将左节点序号赋给值最大节点序号 if (left arr[largest]) { largest = left; } //7.如果右节点存在并且右节点的值大于最大值节点的值,则将右节点序号赋给值最大节点序号 if (right arr[largest]) { largest = right; } //8.上述两个判断,其实就是为了找到三个节点中,值最大的序号的值largest; if (largest != i) { //9.i和largest不相等,说明i,right,left三个节点中,其中一个子节点(left或者right)比父节点i大,因为是大顶堆,此时要交换父节点和最大子节点的值 swap(arr, i, largest); //10.由于交换了父亲节点和其中一个子的位置,所以被交换成父亲值的子节点可能不满足最大堆的要求,因此重建该子节点的堆结构 //注意:此时的largest序号处变成了父亲节点的值,也就是说,他已经不再是最大值!! reBuildHeap(arr, largest, len); } } /** * 值交换函数 * * @param arr * @param i * @param j */ private static void swap(int[] arr, int i, int j) { int temp = arr[i]; arr[i] = arr[j]; arr[j] = temp; } }
5.总结
要完全理解堆排序需要深刻搞懂一下几点
a.什么是堆
b.堆排序的思想
c.序号最大的非叶子节点的计算原理
d.怎么将堆顶元素提取出来
f.提取出堆顶元素后,剩下的元素怎么再构建成堆
备注:文章中的图都是从网上找的,代码也是参考敲了一遍,理解了再敲一遍更容易理解~