Strassen算法及其python实现
2020-12-13 14:21
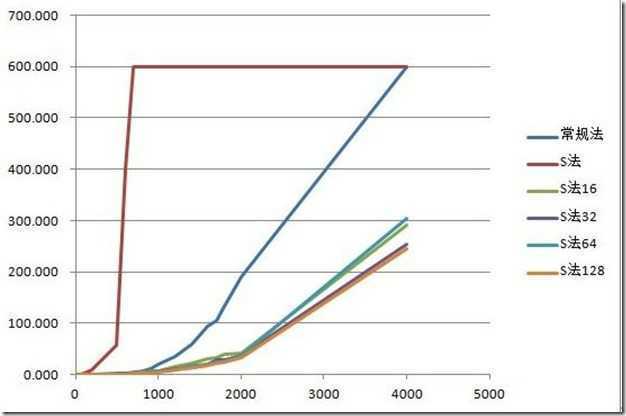
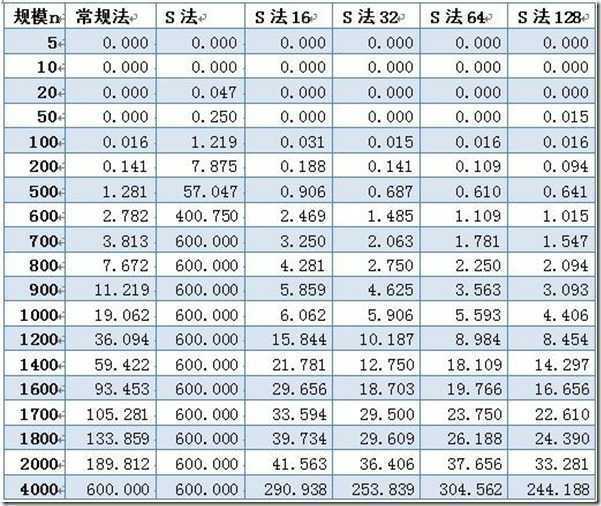
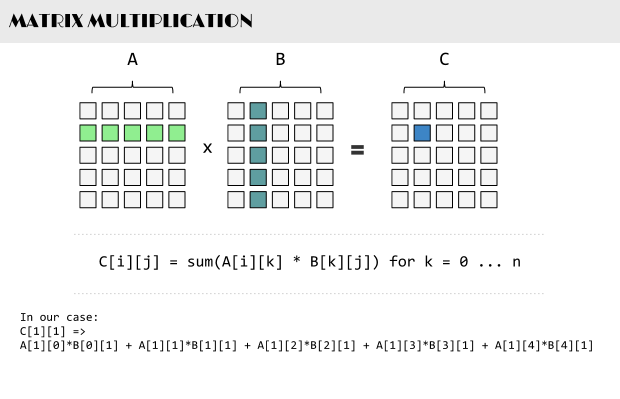
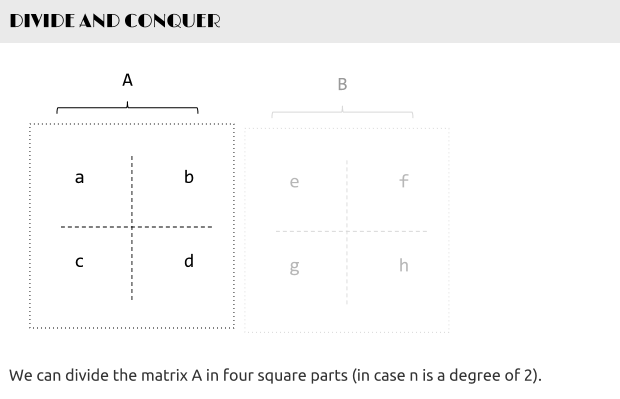
标签：描述 and 设置 pen line 矩阵相乘 lob 渐进 div 请编程实现矩阵乘法，并考虑当矩阵规模较大时的优化方法。 根据wikipedia上的介绍：两个矩阵的乘法仅当第一个矩阵B的列数和另一个矩阵A的行数相等时才能定义。如A是m×n矩阵和B是n×p矩阵，它们的乘积AB是一个m×p矩阵，它的一个元素其中 1 ≤ i ≤ m, 1 ≤ j ≤ p。 值得一提的是，矩阵乘法满足结合律和分配率，但并不满足交换律，如下图所示的这个例子，两个矩阵交换相乘后，结果变了： 下面咱们来具体解决这个矩阵相乘的问题。 其实，通过前面的分析，我们已经很明显的看出，两个具有相同维数的矩阵相乘，其复杂度为O（n^3），参考代码如下： 在解法一中，我们用了3个for循环搞定矩阵乘法，但当两个矩阵的维度变得很大时，O（n^3）的时间复杂度将会变得很大，于是，我们需要找到一种更优的解法。 一般说来，当数据量一大时，我们往往会把大的数据分割成小的数据，各个分别处理。遵此思路，如果丢给我们一个很大的两个矩阵呢，是否可以考虑分治的方法循序渐进处理各个小矩阵的相乘，因为我们知道一个矩阵是可以分成更多小的矩阵的。 如下图，当给定一个两个二维矩阵A B时： 这两个矩阵A B相乘时，我们发现在相乘的过程中，有8次乘法运算，4次加法运算： 矩阵乘法的复杂度主要就是体现在相乘上，而多一两次的加法并不会让复杂度上升太多。故此，我们思考，是否可以让矩阵乘法的运算过程中乘法的运算次数减少，从而达到降低矩阵乘法的复杂度呢？答案是肯定的。 1969年，德国的一位数学家Strassen证明O（N^3）的解法并不是矩阵乘法的最优算法，他做了一系列工作使得最终的时间复杂度降低到了O(n^2.80)。 他是怎么做到的呢？还是用上文A B两个矩阵相乘的例子，他定义了7个变量： 如此，Strassen算法的流程如下： 表面上看，Strassen算法仅仅比通用矩阵相乘算法好一点，因为通用矩阵相乘算法时间复杂度是 对以下要求，计算结果为： 性能分析： 数据取600位上界，即超过10分钟跳出。可以看到使用Strassen算法时，耗时不但没有减少，反而剧烈增多，在n=700时计算时间就无法忍受。仔细研究后发现，采用Strassen算法作递归运算，需要创建大量的动态二维数组，其中分配堆内存空间将占用大量计算时间，从而掩盖了Strassen算法的优势。于是对Strassen算法做出改进，设定一个界限。当n
改进后算法优势明显，就算时间大幅下降。之后，针对不同大小的界限进行试验。在初步试验中发现，当数据规模小于1000时，下界S法的差别不大，规模大于1000以后，n取值越大，消耗时间下降。最优的界限值在32～128之间。 因为计算机每次运算时的系统环境不同（CPU占用、内存占用等），所以计算出的时间会有一定浮动。虽然这样，试验结果已经能得出结论Strassen算法比常规法优势明显。使用下界法改进后，在分治效率和动态分配内存间取舍，针对不同的数据规模稍加试验可以得到一个最优的界限。 小结： 1）采用Strassen算法作递归运算，需要创建大量的动态二维数组，其中分配堆内存空间将占用大量计算时间，从而掩盖了Strassen算法的优势 2）于是对Strassen算法做出改进，设定一个界限。当n
3）矩阵乘法一般意义上还是选择的是朴素的方法，只有当矩阵变稠密，而且矩阵的阶数很大时，才会考虑使用Strassen算法。 ref:https://www.jianshu.com/p/dc67e4a3c841 Strassen算法及其python实现 标签：描述 and 设置 pen line 矩阵相乘 lob 渐进 div 原文地址：https://www.cnblogs.com/wind-chaser/p/11559525.html题目描述
思路分析
解法一、暴力解法
1 //矩阵乘法，3个for循环搞定
2 void Mul(int** matrixA, int** matrixB, int** matrixC)
3 {
4 for(int i = 0; i 2; ++i)
5 {
6 for(int j = 0; j 2; ++j)
7 {
8 matrixC[i][j] = 0;
9 for(int k = 0; k 2; ++k)
10 {
11 matrixC[i][j] += matrixA[i][k] * matrixB[k][j];
12 }
13 }
14 }
15 }
解法二、Strassen算法
；
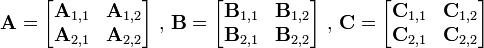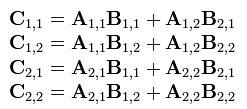
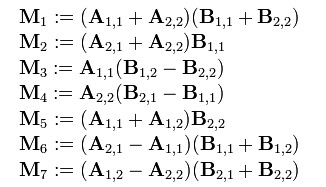
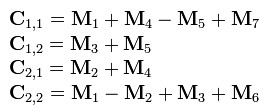
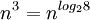，而Strassen算法复杂度只是
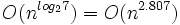。但随着n的变大，比如当n >> 100时，Strassen算法是比通用矩阵相乘算法变得更有效率。 1 # coding=utf-8
2 # copyright@zhangwenchi at 2019/9/21
3 import numpy as np
4
5
6 num_addorsub=0
7 num_mul=0
8 num_assign=0
9
10 def read_matrix(file_path):
11 input_matrix = list()
12 with open(file_path, ‘r‘) as f:
13 txt = f.read()
14 for line in txt.split(‘\n‘):
15 input_matrix.extend(line.split())
16 matrix = [list() for i in range(0, 6)]
17 for i in range(0, 6):
18 for j in range(0, 6):
19 matrix[i].append(float(input_matrix[i * 6 + j]))
20 return matrix
21
22 def matrix_add(matrix_a, matrix_b):
23 ‘‘‘
24 :param matrix_a:
25 :param matrix_b:
26 :return:matrix_c=matrix_a+matrix_b
27 ‘‘‘
28 rows = len(matrix_a) # get numbers of rows
29 columns = len(matrix_a[0]) # get numbers of cols
30 matrix_c = [list() for i in range(rows)] # build matrix 2d list
31 for i in range(rows):
32 for j in range(columns):
33 matrix_c_temp = matrix_a[i][j] + matrix_b[i][j]
34 global num_addorsub,num_assign
35 num_addorsub=num_addorsub+1
36 num_assign = num_assign+1
37 matrix_c[i].append(matrix_c_temp)
38 return matrix_c
39
40
41 def matrix_minus(matrix_a, matrix_b):
42 ‘‘‘
43 :param matrix_a:
44 :param matrix_b:
45 :return:matrix_c=matrix_a-matrix_b
46 ‘‘‘
47 rows = len(matrix_a)
48 columns = len(matrix_a[0])
49 matrix_c = [list() for i in range(rows)]
50 for i in range(rows):
51 for j in range(columns):
52 matrix_c_temp = matrix_a[i][j] - matrix_b[i][j]
53 global num_addorsub,num_assign
54 num_addorsub = num_addorsub + 1
55 num_assign=num_assign+1
56 matrix_c[i].append(matrix_c_temp)
57 return matrix_c
58
59
60 def matrix_divide(matrix_a, row, column):
61 ‘‘‘
62 :param matrix_a:
63 :param row:
64 :param column:
65 :return: matrix_b=matrix_a(row,column) to divide matrix_a
66 ‘‘‘
67 length = len(matrix_a)
68 matrix_b = [list() for i in range(length // 2)]
69 k = 0
70 for i in range((row - 1) * length // 2, row * length // 2):
71 for j in range((column - 1) * length // 2, column * length // 2):
72 matrix_c_temp = matrix_a[i][j]
73 matrix_b[k].append(matrix_c_temp)
74 k += 1
75 return matrix_b
76
77
78 def matrix_merge(matrix_11, matrix_12, matrix_21, matrix_22):
79 ‘‘‘
80 :param matrix_11:
81 :param matrix_12:
82 :param matrix_21:
83 :param matrix_22:
84 :return:mariix merged by 4 parts above
85 ‘‘‘
86 length = len(matrix_11)
87 matrix_all = [list() for i in range(length * 2)] # build a matrix of double rows
88 for i in range(length):
89 # for each row. matrix_all list contain row of matrix_11 and matrix_12
90 matrix_all[i] = matrix_11[i] + matrix_12[i]
91 for j in range(length):
92 # for each row. matrix_all list contain row of matrix_21 and matrix_22
93 matrix_all[length + j] = matrix_21[j] + matrix_22[j]
94 return matrix_all
95
96
97 def strassen(matrix_a, matrix_b):
98 ‘‘‘
99 :param matrix_a:
100 :param matrix_b:
101 :return:matrix_a * matrix_b
102 ‘‘‘
103 rows = len(matrix_a)
104 if rows == 1:
105 matrix_all = [list() for i in range(rows)]
106 matrix_all[0].append(matrix_a[0][0] * matrix_b[0][0])
107 elif(rows % 2 ==1):
108 matrix_a_np = np.array(matrix_a)
109 matrix_b_np = np.array(matrix_b)
110 matrix_all = np.dot(matrix_a_np,matrix_b_np)
111 global num_mul,num_addorsub
112 num_mul = num_mul + 27
113 num_addorsub=num_addorsub + 18
114 else:
115 # 10 first parts of computing
116 s1 = matrix_minus((matrix_divide(matrix_b, 1, 2)), (matrix_divide(matrix_b, 2, 2)))
117 s2 = matrix_add((matrix_divide(matrix_a, 1, 1)), (matrix_divide(matrix_a, 1, 2)))
118 s3 = matrix_add((matrix_divide(matrix_a, 2, 1)), (matrix_divide(matrix_a, 2, 2)))
119 s4 = matrix_minus((matrix_divide(matrix_b, 2, 1)), (matrix_divide(matrix_b, 1, 1)))
120 s5 = matrix_add((matrix_divide(matrix_a, 1, 1)), (matrix_divide(matrix_a, 2, 2)))
121 s6 = matrix_add((matrix_divide(matrix_b, 1, 1)), (matrix_divide(matrix_b, 2, 2)))
122 s7 = matrix_minus((matrix_divide(matrix_a, 1, 2)), (matrix_divide(matrix_a, 2, 2)))
123 s8 = matrix_add((matrix_divide(matrix_b, 2, 1)), (matrix_divide(matrix_b, 2, 2)))
124 s9 = matrix_minus((matrix_divide(matrix_a, 1, 1)), (matrix_divide(matrix_a, 2, 1)))
125 s10 = matrix_add((matrix_divide(matrix_b, 1, 1)), (matrix_divide(matrix_b, 1, 2)))
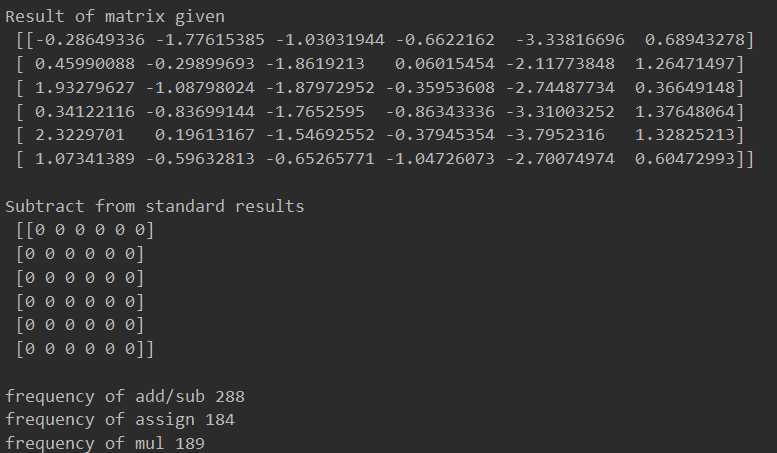
126 # 7 second parts of computing
127 p1 = strassen(matrix_divide(matrix_a, 1, 1), s1)
128 p2 = strassen(s2, matrix_divide(matrix_b, 2, 2))
129 p3 = strassen(s3, matrix_divide(matrix_b, 1, 1))
130 p4 = strassen(matrix_divide(matrix_a, 2, 2), s4)
131 p5 = strassen(s5, s6)
132 p6 = strassen(s7, s8)
133 p7 = strassen(s9, s10)
134 # 4 final parts of result
135 c11 = matrix_add(matrix_add(p5, p4), matrix_minus(p6, p2))
136 c12 = matrix_add(p1, p2)
137 c21 = matrix_add(p3, p4)
138 c22 = matrix_minus(matrix_add(p5, p1), matrix_add(p3, p7))
139 matrix_all = matrix_merge(c11, c12, c21, c22)
140 global num_assign
141 num_assign =num_assign+22
142 return matrix_all
143
144
145 def main():
146 # read data
147 A = read_matrix(‘matrixA.txt‘)
148 B = read_matrix(‘matrixB.txt‘)
149
150 # compute A*B
151 C = strassen(A,B)
152 print("\nResult of matrix given\n",np.array(C))
153
154 # verificate A*B
155 C_verification=np.dot(A,B)
156 print("\nSubtract from standard results\n",np.array((C-C_verification),dtype=int))
157
158 # statistical data
159 print("\nfrequency of add/sub",num_addorsub)
160 print("frequency of assign", num_assign)
161 print("frequency of mul", num_mul)
162
163 new_matrixA = np.random.random_integers(-5,5,size=(8, 8))
164 print("\nRandom Matrix A:\n", new_matrixA)
165 new_matrixB = np.random.random_integers(-5,5,size=(8, 8))
166 print("\nRandom Matrix B:\n", new_matrixB)
167
168 AdotB=strassen(new_matrixA, new_matrixB)
169 print("\n A*B Result of matrixs by generate randomly\n",np.array(AdotB))
170
171 BdotA = strassen(new_matrixB, new_matrixA)
172 print("\n B*A Result of matrixs by generate randomly\n", np.array(BdotA))
173
174 result=new_matrixA
175 for i in range(0,2019):
176 result=strassen(result,new_matrixA)
177 print("\n A^2019 Result of matrixs by generate randomly\n",np.array(result))
178 if __name__ == ‘__main__‘:
179 main()
