Kruskal算法 (克鲁斯卡尔)
2020-12-13 15:13
标签:font 依次 amp color int 放弃 auto 必须 顶点 Kruskal算法是一种用来查找最小生成树的算法。 树:如果一个无向连通图中不存在回路,则这种图称为树。 生成树 :无向连通图G的一个子图如果是一颗包含G的所有顶点的树,则该子图称为G的生成树。 生成树是连通图的极小连通子图。这里所谓极小是指:若在树中任意增加一条边,则将出现一条回路;若去掉一条边,将会使之变成非连通图。 最小生成树:对无向连通图的生成树,各边的权值总和称为生成树的权,权最小的生成树称为最小生成树。 构成生成树的准则有三条: ① 必须只使用该网络中的边来构造最小生成树。 ② 必须使用且仅使用n-1条边来连接网络中的n个顶点 ③ 不能使用产生回路的边。 ① 将原图中每条边的权值进行从小到大排序。 ② 从小到大依次判断每条边。 若当前边不会与当前的最小生成树形成回路,则将当前边加入当前的最小生成树。 反之,则放弃该边,继续判断下一条边。 直到选择了(顶点数-1)条边为止,此时的生成树为最小生成树。(一般利用并查集判断是否形成回路) ① 排序 ②从小到大判断每条边。 代码 Kruskal算法 (克鲁斯卡尔) 标签:font 依次 amp color int 放弃 auto 必须 顶点 原文地址:https://www.cnblogs.com/VividBinGo/p/11576064.html定义
准备
实现
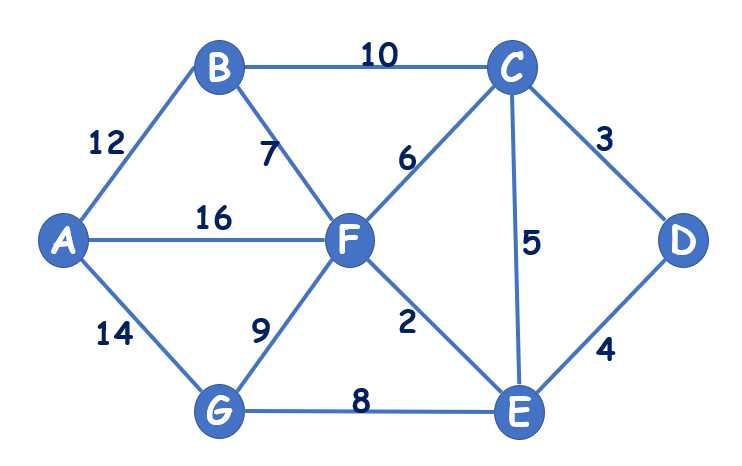
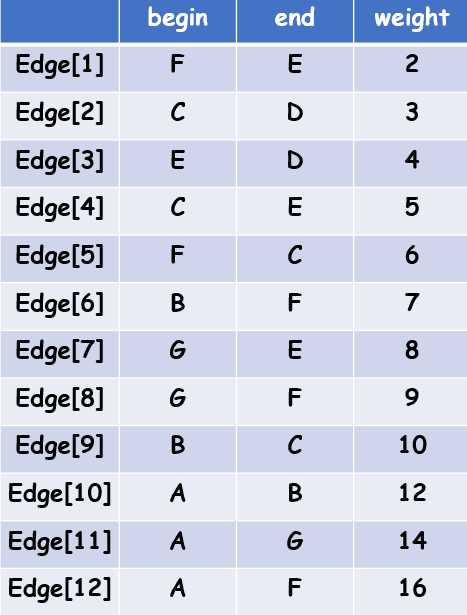
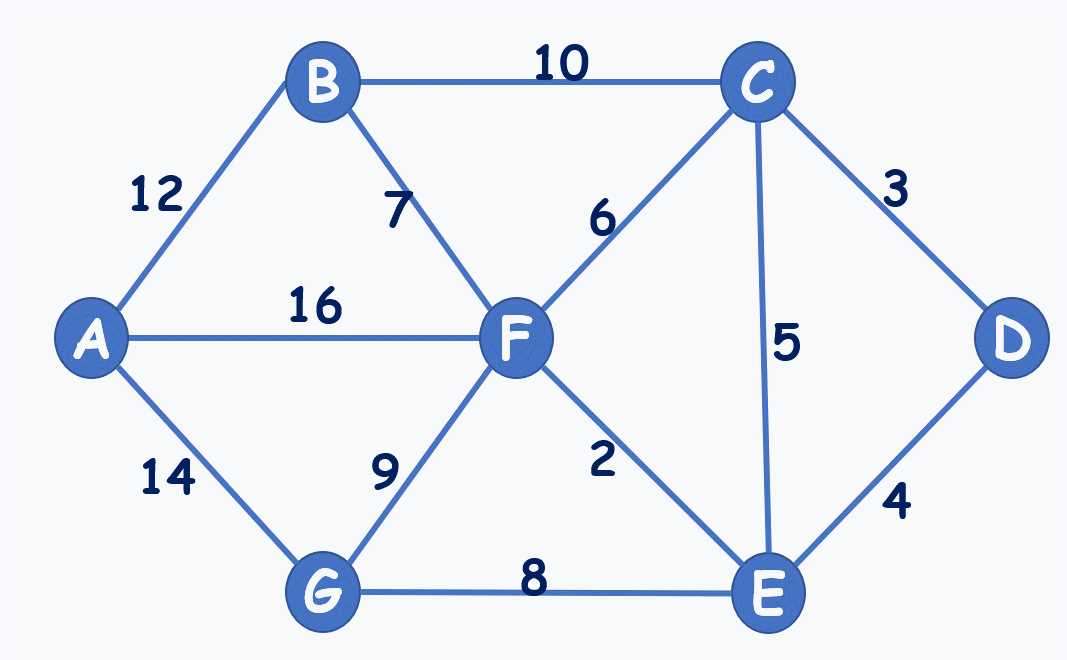
#include