图论基础——邻接链表存图+拓扑排序
2020-12-13 16:12
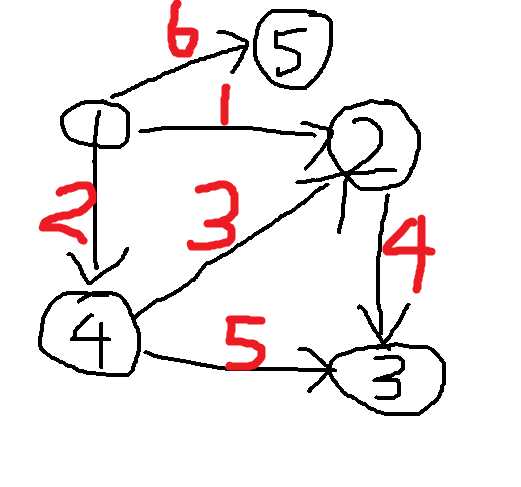
标签:有向无环图 body scan 链式存储 情况 dir ext image width 邻接链表存图,在这里其实是用数组进行模拟的 又叫做链式存储法,本来是要用链表实现的,但大多数情况下只需要用数组模拟即可 例: 话不多说,直接上代码 注:e[i]为一个结构体,负责记录每一条边的信息 总的来说,这是一种存图的方法,更是图论的基础 拓扑排序 拓扑排序是对有向无环图(Directed Acyclic Graph简称DAG)求出一个顶点序列,使其满足:对于任意边(u,v)?E,u在序列的位置总在v之前。 另外在需要最大和最小拓扑序时,就要用到优先队列来存入 代码主体差不多,只是优先队列定义与栈不同罢了 图论基础——邻接链表存图+拓扑排序 标签:有向无环图 body scan 链式存储 情况 dir ext image width 原文地址:https://www.cnblogs.com/jhl0824/p/11618429.html
u(边的起点)
v(边的终点)
w(边的权值)
4
2
1
1
2
3
1
4
1
1
5
2
4
3
4
2
3
1
for(int i=1;i)
{
scanf("%d%d%d",&u1,&v1,&w1);
e[i].u =u1;//赋给第i条边的起点
e[i].v =v1;//赋给第i条边的终点
e[i].w =w1;//赋给第i条边的权值
e[i].next =head[u1];//现在这条边的上一条边=现在这条边的起点的上一条边(u1是起点)
head[u1]=i;//于是,对于以后的边来说,现在这条边就是起点的上一条边 }
struct Node{
int u;//边的起点
int v;//边的终点
int w;//边的权值
int next;//边的上一条边(用于连接)
}e[边的最大条数];
bool topsort()//拓扑排序,有拓扑序返回真,否则返回假
{
int p,q;
for(int i=1;i//先找到入度为0的节点入栈
{
if(!d[i])s.push(i);//d[i]表示i点的入度,在加边的时候初始化d[i]
}
while(!s.empty())//当栈非空进行操作
{
p=s.top();//记录栈顶节点
s.pop();//弹出栈顶节点
ans[cnt++]=p;//将弹出节点存储到结果数组,并计数
for(int i=head[p];i!=-1;i=e[i].next)//清除该节点的出度
{
q=e[i].v;
if(!(--d[q]))s.push(q);//如果又发现入度为0的节点,继续入栈
}
}
if(cntreturn false;//当有节点没入栈,则说明存在环
return true;
}