[CSP-S模拟测试]:Rectangle（模拟+树状数组）

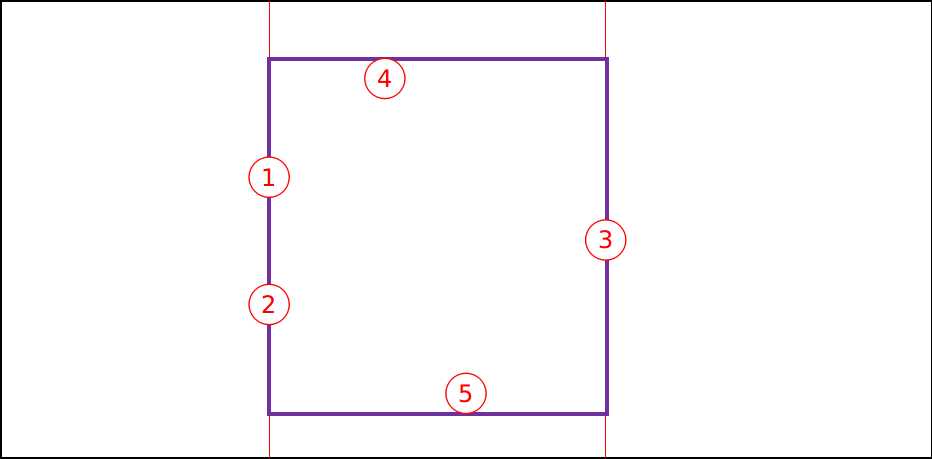
标签：out   rectangle   space   flag   顶点   没有   $0   坐标   sla   

题目描述

平面上有$n$个点，第$i$个点的坐标为$X_i,Y_i$。对于其中的一个非空点集$S$，定义$f(S)$为一个最小矩形，满足：
$\bullet$覆盖$S$中所有的点（在边界上也算覆盖）；
$\bullet$边与坐标轴平行。
求所有不同的$f(S)$的面积和对$10^9+7$取模的结果。两个矩形被认为是不同的，当且仅当它们顶点坐标不同。

输入格式

从文件$rectangle.in$中读入数据。
第一行一个整数$n$。
接下来$n$行，每行两个整数$X_i,Y_i$。

输出格式

输出到文件$rectangle.out$中。
一行一个整数表示答案。

样例

样例输入：

4
1 2
3 1
4 4
5 1

样例输出：

45

数据范围与提示

样例解释：

有$8$个面积大于$0$的不同矩形，以下是它们左下角和右上角的坐标：
$(1,1),(3,2);(1,1),(4,4);(1,1),(5,2);(1,1),(5,4)$
$(1,2),(4,4);(3,1),(4,4);(3,1),(5,4);(4,1),(5,4)$

数据范围：

对于所有数据，满足$2\leqslant n\leqslant 10^4,1\leqslant X_i,Y_i\leqslant 2500$，没有重复的点。
$\bullet Subtask1(13\%)$，$n\leqslant 18$。
$\bullet Subtask2(9\%)$，$n\leqslant 50$。
$\bullet Subtask3(25\%)$，$n\leqslant 300$。
$\bullet Subtask4(21\%)$，$n\leqslant 2500,X_i\neq X_j,Y_i\neq Y_j$。
$\bullet Subtask5(19\%)$，$n\leqslant 2500$。
$\bullet Subtask6(13\%)$，没有特殊的约束。

题解

先来考虑$21\%$的$X_i\neq X_j,Y_i\neq Y_j$的情况。

我们可以$n^2$枚举左右边界，那么设边界上的点为$(L,y_1)$和$(R,y_2)$。

那么只有位于$(L,R)$且纵坐标$>\max(y_1,y_2)$和$

现在来考虑一般情况，每个$L$和$R$上可能有很多的点，我们依次枚举计数即可。

但是可能会出现如下图中的情况：

显然，我们在统计答案点$1,3$和点$2,3$的贡献的时候会将紫色矩阵算重，不用担心，我们只需要将纵坐标最靠下的统计就好了。

代码实现稍繁琐。

时间复杂度：$\Theta(nm\log m)$。

期望得分：$100$分。

实际得分：$100$分。

代码时刻

#include
using namespace std;
const int mod=1000000007;
int n;
int Map[2501][2501];
int tr[2][2501][2501];
bool vis[2501][2501];
long long ans;
int lowbit(int x){return x&-x;}
void add(int id,int k,int x,int w)
{
	for(int i=x;i

rp++

[CSP-S模拟测试]:Rectangle（模拟+树状数组）

标签：out   rectangle   space   flag   顶点   没有   $0   坐标   sla   

原文地址：https://www.cnblogs.com/wzc521/p/11619495.html