堆排序(选择排序)
2020-12-13 16:26
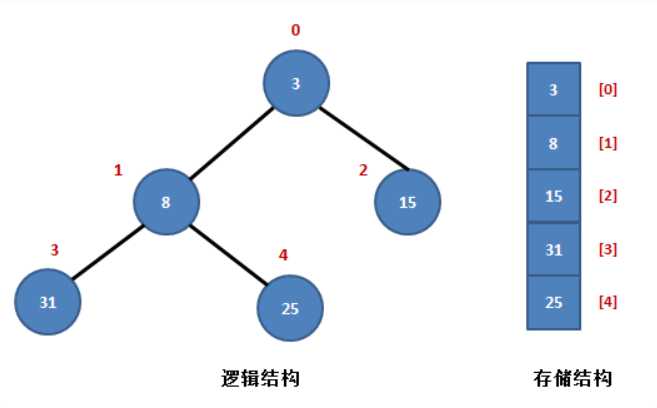
标签:交换 排序 img ima src 处理 str http alt 堆是一棵顺序存储的完全二叉树。 其中每个结点的关键字都不大于其孩子结点的关键字,这样的堆称为小根堆。 其中每个结点的关键字都不小于其孩子结点的关键字,这样的堆称为大根堆。 举例来说,对于n个元素的序列{R0, R1, ... , Rn}当且仅当满足下列关系之一时,称之为堆: (1) Ri 且 Ri 小根堆) (2) Ri >= R2i+1 且 Ri >= R2i+2 (大根堆) 其中i=1,2,…,n/2向下取整; 如上图所示,序列R{3, 8, 15, 31, 25}是一个典型的小根堆。 堆中有两个父结点,元素3和元素8。 元素3在数组中以R[0]表示,它的左孩子结点是R[1],右孩子结点是R[2]。 元素8在数组中以R[1]表示,它的左孩子结点是R[3],右孩子结点是R[4],它的父结点是R[0]。可以看出,它们满足以下规律: 设当前元素在数组中以R[i]表示,那么, (1) 它的左孩子结点是:R[2*i+1]; (2) 它的右孩子结点是:R[2*i+2]; (3) 它的父结点是:R[(i-1)/2]; (4) R[i]
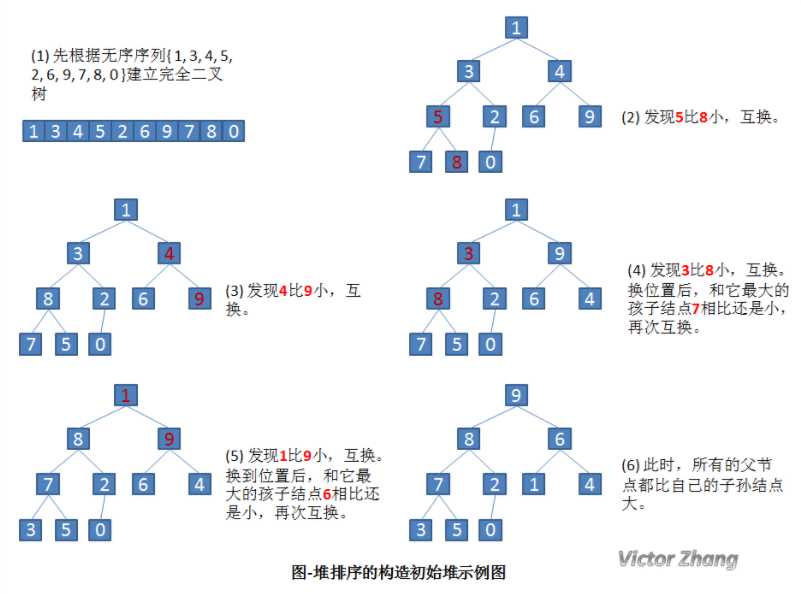
2 重点 首先,按堆的定义将数组R[0..n]调整为堆(这个过程称为创建初始堆),交换R[0]和R[n]; 然后,将R[0..n-1]调整为堆,交换R[0]和R[n-1]; 如此反复,直到交换了R[0]和R[1]为止。 以上思想可归纳为两个操作: (1)根据初始数组去构造初始堆(构建一个完全二叉树,保证所有的父结点都比它的孩子结点数值大)。 (2)每次交换第一个和最后一个元素,输出最后一个元素(最大值),然后把剩下元素重新调整为大根堆。 当输出完最后一个元素后,这个数组已经是按照从小到大的顺序排列了。 先通过详细的实例图来看一下,如何构建初始堆。 设有一个无序序列 { 1, 3, 4, 5, 2, 6, 9, 7, 8, 0 }。 构造了初始堆后,我们来看一下完整的堆排序处理: 还是针对前面提到的无序序列 { 1, 3, 4, 5, 2, 6, 9, 7, 8, 0 } 来加以说明。 堆排序(选择排序) 标签:交换 排序 img ima src 处理 str http alt 原文地址:https://www.cnblogs.com/carpeak/p/11619849.html1 堆的概念