算法-03 | 深度优先DFS| 广度优先BFS
2020-12-20 02:36
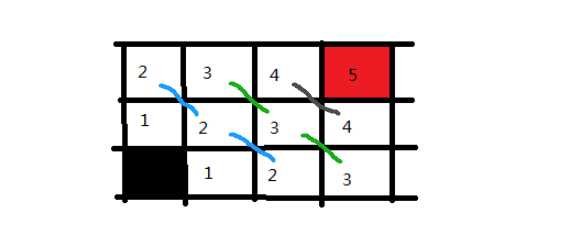
标签:level ext 选择 回溯思想 ase ide was git 回溯 在树(图/状态集)中寻找特定节点 深度优先搜索算法和广度优先搜索算法都是基于“图”这种数据结构。 图上的搜索算法就是,在图中找出从一个顶点出发,到另一个顶点的路径。图上的搜索算法有深度优先、广度优先搜索算法,和A*A∗、IDA*IDA∗ 等启发式搜索算法。 广度优先搜索和深度优先搜索是图上的两种最常用、最基本的搜索算法,仅适用于状态空间不大的搜索。它们比A*A∗、IDA*IDA∗ 等启发式搜索算法要简单粗暴,没有什么优化,所以也叫作暴力搜索算法。 广度优先搜索,采用地毯式层层推进,从起始顶点开始,依次往外遍历。广度优先搜索需要借助队列来实现,遍历得到的路径就是起始顶点到终止顶点的最短路径。 深度优先搜索,采用回溯思想,适合用递归或栈来实现。遍历得到的路径并不是最短路径。 深度优先和广度优先搜索的时间复杂度都是 O(E),空间复杂度都是 O(V)。其中E代表边,O代表顶点。 - 深度优先:depth first search 还有是按照优先级优先进行搜索,(可按现实场景进行定义,更适合于现实中很多的业务场景。这种算法称为 启发式搜索) “走迷宫”。假设你站在迷宫的某个岔路口,然后想找到出口。你随意选择一个岔路口来走,走着走着发现走不通的时候,你就回退到上一个岔路口,重新选择一条路继续走,直到最终找到出口。这种走法就是一种深度优先搜索策略。实线箭头表示遍历,虚线箭头表示回退。但深度优先搜索最先找出来的路径,并不是顶点 s 到顶点 t 的最短路径。深度优先搜索用的是回溯思想,回溯思想非常适合用递归来实现。 黑色表起始点,红色表终点。按照左下右上的方向顺序走,即,如果左边可以走,我们先走左边。然后递归下去,没达到终点或者走不通了,回溯上一个位置...... 首先往左走,走不通了就回溯到上一步(左右都走过了再回溯)、上一步到起点,按左下右上的顺序走。 遍历顺序 : 用栈 DFS python代码模板 广度优先搜索(Breadth-First-Search),简称 BFS。它是一种“地毯式”层层推进的搜索策略,即先查找离起始顶点最近的,然后是次近的,依次往外搜索: 广度优先搜索较之深度优先搜索之不同在于,深度优先搜索旨在不管有多少条岔路,先一条路走到底,不成功就返回上一个路口然后就选择下一条岔路,而广度优先搜索旨在面临一个路口时,把所有的岔路口都记下来,然后选择其中一个进入,然后将它的分路情况记录下来,然后再返回来进入另外一个岔路,并重复这样的操作。 顺序遍历: 用队列 BFS的python代码模板: https://www.geeksforgeeks.org/difference-between-bfs-and-dfs/ A Tree is typically traversed in two ways: All four traversals require O(n) time as they visit every node exactly once. here is difference in terms of extra space required. https://xiaqiu2233.github.io/2017/10/04/%E4%BA%8C%E5%8F%89%E6%A0%91%E7%9A%84%E5%B9%BF%E5%BA%A6%E5%92%8C%E6%B7%B1%E5%BA%A6%E4%BC%98%E5%85%88%E9%81%8D%E5%8E%86%EF%BC%88%E5%85%88%E5%BA%8F%E3%80%81%E4%B8%AD%E5%BA%8F%E3%80%81%E5%90%8E%E5%BA%8F%EF%BC%89/ https://www.geeksforgeeks.org/bfs-vs-dfs-binary-tree/ 算法-03 | 深度优先DFS| 广度优先BFS 标签:level ext 选择 回溯思想 ase ide was git 回溯 原文地址:https://www.cnblogs.com/shengyang17/p/13264349.html1. 搜索算法
搜索 -- 遍历
- 广度优先:breadth first search2. 深度优先搜索
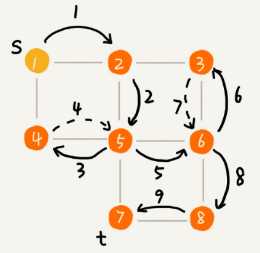
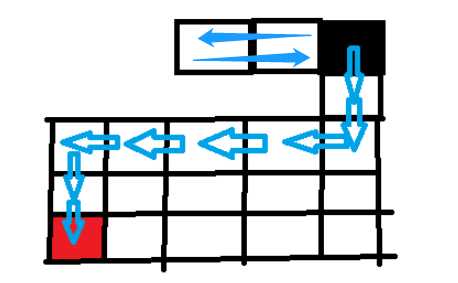
深度优先搜索 Depth-First-Search
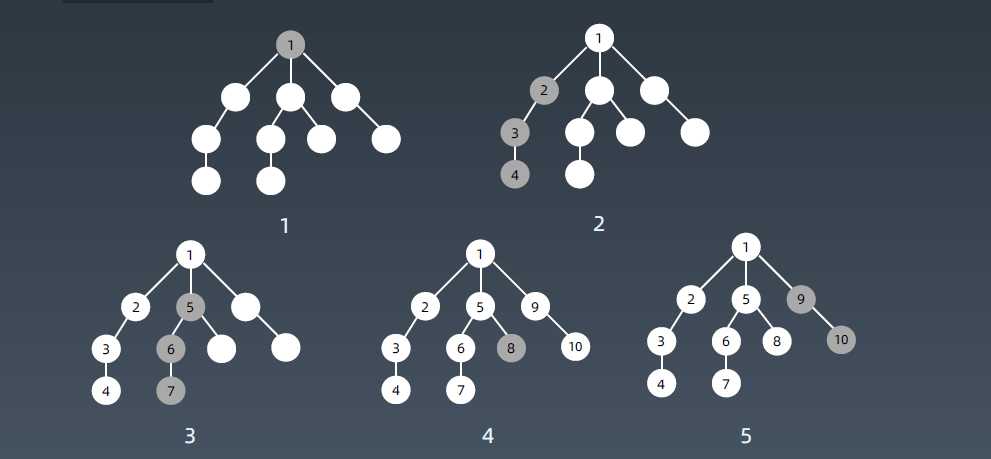
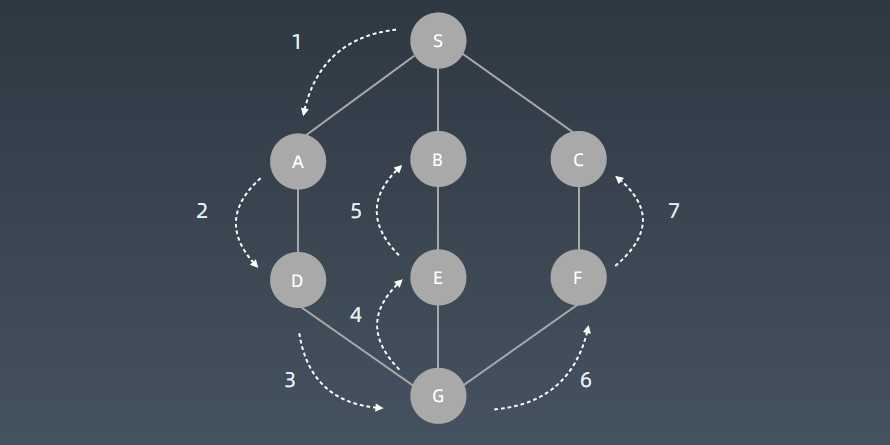


DFS 代码 - 递归写法
visited = set()
def dfs(node, visited):
if node in visited: # terminator
# already visited
return
visited.add(node)
# process current node here.
...
for next_node in node.children():
if not next_node in visited:
dfs(next_node, visited)
DFS 代码 - 非递归写法
def DFS(self, tree):
if tree.root is None:
return []
visited, stack = [], [tree.root]
while stack:
node = stack.pop()
visited.add(node)
process (node)
nodes = generate_related_nodes(node)
stack.push(nodes)
# other processing work
...
3. 广度优先搜索 Breadth-First-Search
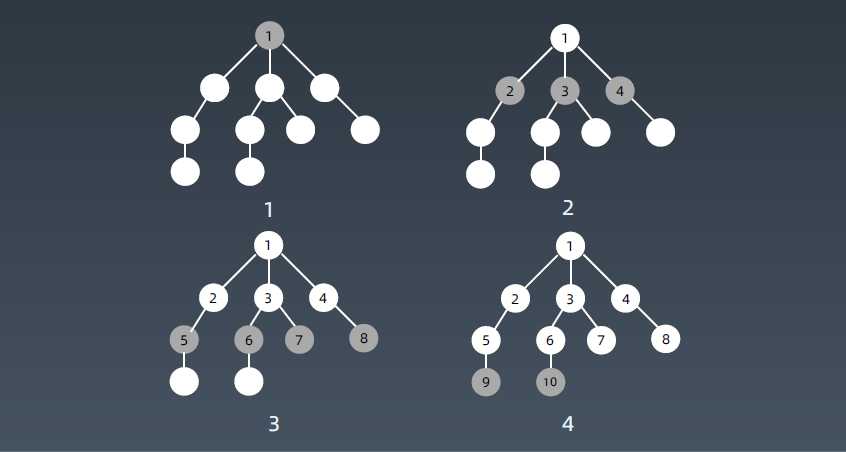
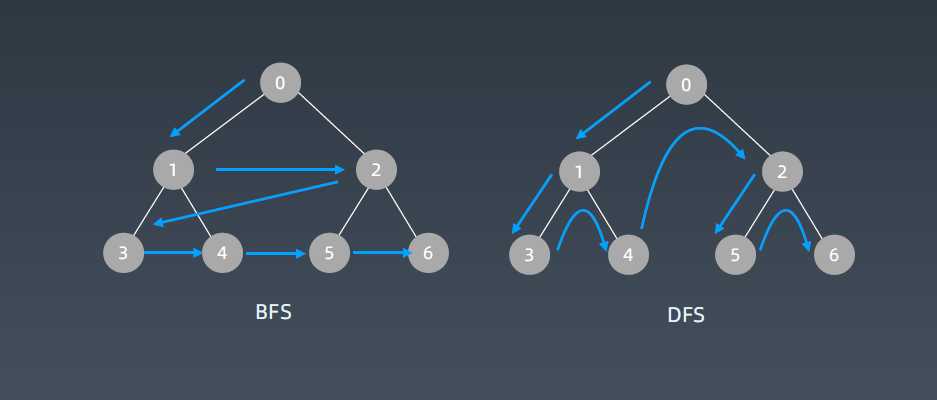


BFS 代码
def BFS(graph, start, end):
queue = []
queue.append([start])
visited.add(start)
while queue:
node = queue.pop()
visited.add(node)
process(node)
nodes = generate_related_nodes(node)
queue.push(nodes)
# other processing work
...
DFS 代码 - 递归写法
visited = set()
def dfs(node, visited):
visited.add(node)
# process current node here.
...
for next_node in node.children():
if not next_node in visited:
dfs(next node, visited)
4. DFS| BFS 与 Tree的遍历的关系
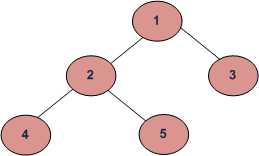
BFS and DFSs of above Tree
Breadth First Traversal : 1 2 3 4 5
Depth First Traversals:
Preorder Traversal : 1 2 4 5 3
Inorder Traversal : 4 2 5 1 3
Postorder Traversal : 4 5 2 3 1
下一篇:C语言计算阶乘和