Boyer-Moore算法
2021-02-19 21:21
标签:优化 == index 规则 存在 原则 com 相同 线性 部分资料来自:https://blog.csdn.net/no_heart2019/article/details/96564763 https://blog.csdn.net/qzp1991/article/details/42663969 https://blog.csdn.net/v_JULY_v/article/details/6545192 https://blog.csdn.net/qq_21201267/article/details/92799488 BM算法被认为是亚线性串匹配算法,它在最坏情况下找到模式所有出现的时间复杂度为O(mn),在最好情况下执行匹配找到模式所有出现的时间复杂度为O(n/m)。 尤其在空格较多的文本中,比KMP算法的实际效能高。 BM算法从模式串的尾部开始匹配,即从后往前 这是BM算法的核心,他有两种跳转方式,分别对应两种规则,而每次跳转多少取决于这两种跳转规则的最大值 当文本串中的某个字符跟模式串的某个字符不匹配时,我们称文本串中的这个失配字符为坏字符,此时模式串需要向右移动 移动的位数 = 坏字符在模式串中的位置 - 坏字符在模式串中最右出现的位置 此外,如果"坏字符"不包含在模式串之中,则最右出现位置为-1。 S失配,而模式串中S的出现在-1(即没有,w的下标为0) 减去相对位置差S->6(当前坏字符位置), S‘->-1(模式串位置), 6-(-1)==7 所以我们后移7步,得到: 如何理解?我们要让字符串匹配成功的必要条件是让这个坏字符要满足情况,所以你肯定优先找到模式串对应的字符与之匹配,让之先满足情况 其次为了防止漏了正确答案,取的是最右位置 如果是不存在,位置给-1,它就整串下移了 这也就是为什么文本中效率比较高,文本空格多,让坏字符出现的可能性更大,频率更高,跳转性以及跳转幅度很可观 进一步使用坏字符原则我们可以得到: 好后缀,指的就是当前以及匹配上的子串 先看图,下面的图很清晰的展现了好后缀规则,我们现在有好后缀bc 通过上图,我们可以总结出来,此规则是: 从好后缀中的所有后缀子串中,找一个最长的的后缀v,并且使得它在模式串中存在相同的子串v‘,v!=v‘,如图: 而后移位数,与坏字符规则类似,当字符失配时,后移位数=v‘的位置-v的位置 注意他和kmp的next不同,思路有相似之处 那么BM算法的核心来了,那么如何求好后缀中最长满足条件的子串嘞? 请看下面预处理部分 坏字符,存每个字符出现在最右边的位置,后移步数可能算出来是负的,但是好规则取值一定是正的,取完max无影响 而好后缀的求解并不像KMP中next数组递推去求解,它求起来细节特别多 首先是暴力求解如下内容,这里复杂度要看模式串情况 注意这里,当好后缀有多个可行的前缀位置,我们从前往后找会产生覆盖,从而我们取的是这些位置当中最右的 很多情况下,好后缀不一定有对应前缀,但它的后缀子串有 所以为了跳转方便,我们不妨进一步再处理一下,suffix为-1的好后缀它们所包含的最长可行子后缀的情况 取好规则与坏规则最大者 注意一下suffix为-1的情况以及匹配成功该如何处理(详见代码) 之前讲了最坏情况下找到模式所有出现的时间复杂度为O(mn),why? 比如说,一个最拉跨例子aaaaaaa匹配aaaaaa...复杂度起飞,不仅预处理会拉垮,而且匹配时也会拉垮 但是在正常文本匹配,如文章中找单词,BM效率优于KMP Boyer-Moore算法 标签:优化 == index 规则 存在 原则 com 相同 线性 原文地址:https://www.cnblogs.com/et3-tsy/p/12683792.htmlBM(Boyer-Moore)
两个规则
坏字符规则(文本中效率高的体现点)


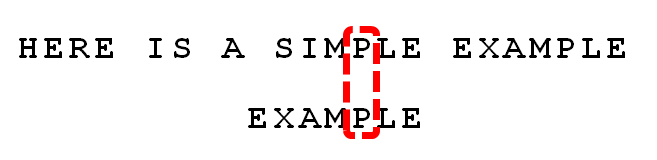
好后缀规则
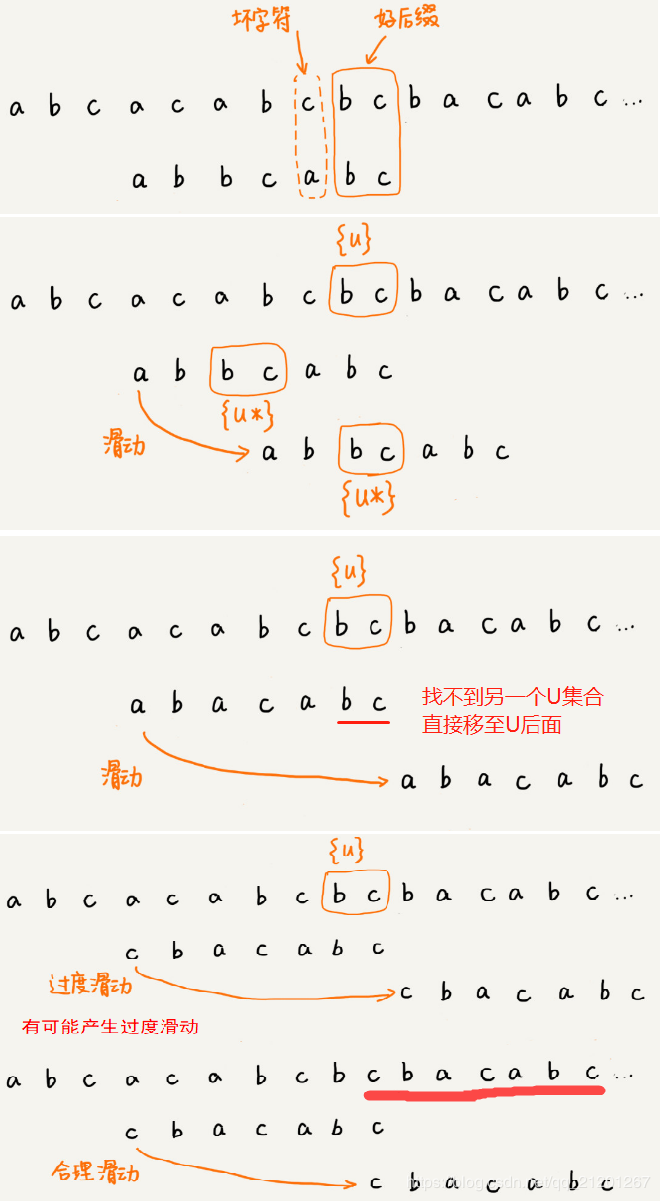
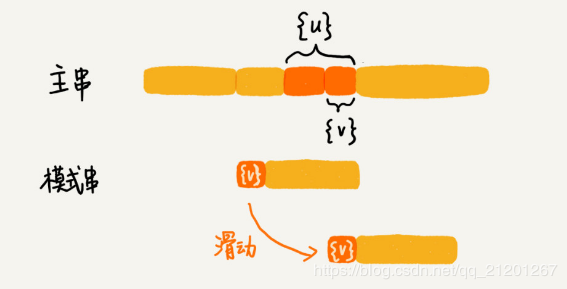
预处理
坏字符
好字符

for(int i=0;iint curpos=-1;
for(int i=1;i匹配
不足
代码
/*
BM算法
统计目标串中模式串的个数
*/
#include
上一篇:java 抽象类和接口
下一篇:Rx Swift5更新