算法图解——找出整形数组里出现一次的两个数
2021-06-05 15:01
标签:pre 结果 解法 很多 数组 后序 span mic return 最近参加了huawei的一个比赛,初赛刚结束,结果未知。虽然过程艰辛,经常搞到夜里1点,但是学到的知识还是挺多的。在学校没有参加很多的比赛也是一种遗憾,不得不说在学校自己的时间是真的多啊。感慨一番,继续造题。加油! 一个整型数组 nums 里除两个数字之外,其他数字都出现了两次。请写程序找出这两个只出现一次的数字。要求时间复杂度是O(n),空间复杂度是O(1)。 示例 1: 输入:nums = [4,1,4,6] 输出:[1,6] 或 [6,1] 示例 2: 输入:nums = [1,2,10,4,1,4,3,3] 输出:[2,10] 或 [10,2] 限制:2
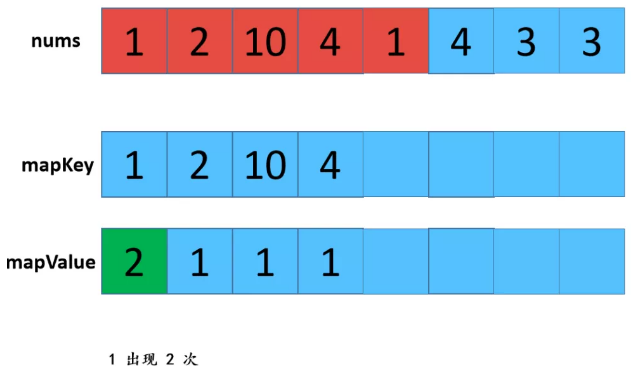
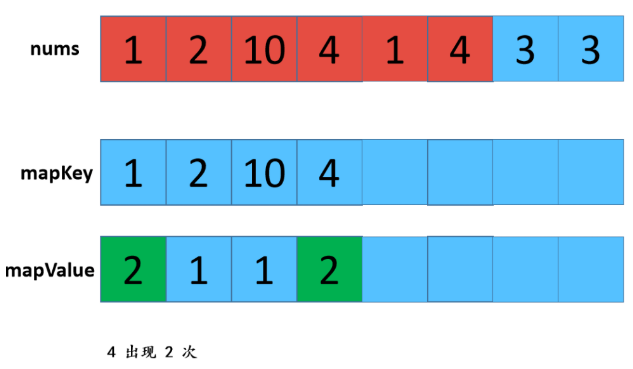
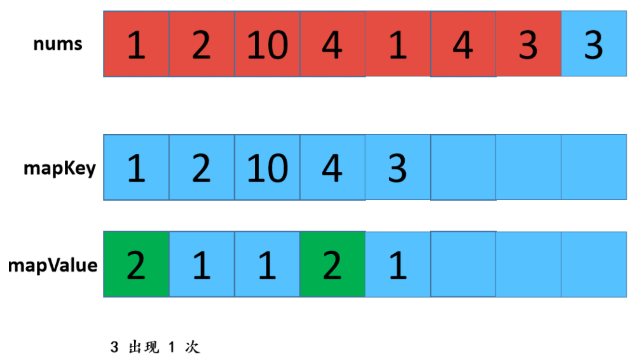
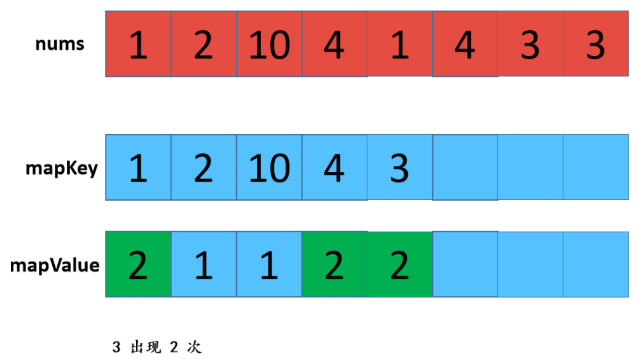
利用HashMap,优缺点:查找效率高,但是有额外空间。 步骤: 1:遍历数组,存放到map中,map中的key是数组中的值,value是该值出现的次数,在这里学到了一个新方法就是hashmap的getOrDefault(); 2:遍历数组,从map中查找对应数值的次数,如果是1则取出,放置返回数组res中。 不知听懂否?没听懂不要紧,“乔哥”(微信公众号:程序员乔戈里)给出了图示: 以上就是遍历数组,将值和值对应出现的次数放在了map中。接下来,就是遍历数组,取出次数为1的数值了。 由于节省篇幅,想看详解的可点击文末链接(每一个步骤都有详细图解噢),再次致谢乔哥,小夕和皮皮。 在这里我只放两张典型的图(出现一次的,出现两次的)。 OK,话不多说。看具体实现: 这个就不放注释了哈: 上面我们也说了,这样虽然能解题,但是我们显然是不满足(条件的),哈哈哈。那么还有其他思路嘛? 刷过剑指offer的童鞋看到这道题应该会稍微熟悉,因为在那本书中,有一个类似的题,说它类似是因为,它的题中是要求出数组中出现一次的单个数值,和这道题不一样的就是这里人家有两个次数为1的值。 但那道题可以利用异或的思路求解,何为异或?就是"^"它了,没错。 相同数字异或为0,不同数字异或为1。那道题的解法是:遍历数组,异或全部元素,最后剩下的就是出现一次的数值,因为出现两次的都异或为0了。 咦?那么我们是不是可以这样想?既然这道题的数组中有两个出现次数为1的数值,那么,如果我们能够把这俩数值分到不同的数组中(也就是一分为二),然后我们在利用该思路,分别对这两个数组进行遍历异或操作,不就可以得到这两个数值了吗? 是滴,没错。所以关键就是如何分组。 思路是这样的:假设遍历完数组后,得到的是a^b,那么我们可以知道a^b这个值中,二进制中,位数为1的位置代表了a和b这两个值的二进制值在该位置的不同(0和1),因为只有该位不同a^b在该位才会为1(根据异或规则)。 那好,我们就根据这个,将a和b分到不同的两个数组中,即:在该位为0的分到一个数组,在该位为1的分到另一个数组。 然后,遍历每个数组,异或数组中所有元素即可。 好了,文字描述完了,还不懂的话请看图解(感谢小夕提供的图解): 好的,中间省略.... 结果分别异或两组数组,可得到 5 和 10 。 再次总结步骤: 【参考及致谢】 1、小夕深夜联系两名知名博主开始搞事情,一起怒刷一道阿里高频面试题,击败100%的用户! Over....... 算法图解——找出整形数组里出现一次的两个数 标签:pre 结果 解法 很多 数组 后序 span mic return 原文地址:https://www.cnblogs.com/gjmhome/p/14624683.html题目:
来源:力扣(LeetCode)
链接:https://leetcode-cn.com/problems/shu-zu-zhong-shu-zi-chu-xian-de-ci-shu-lcof
著作权归领扣网络所有。商业转载请联系官方授权,非商业转载请注明出处。
解析
思路1:

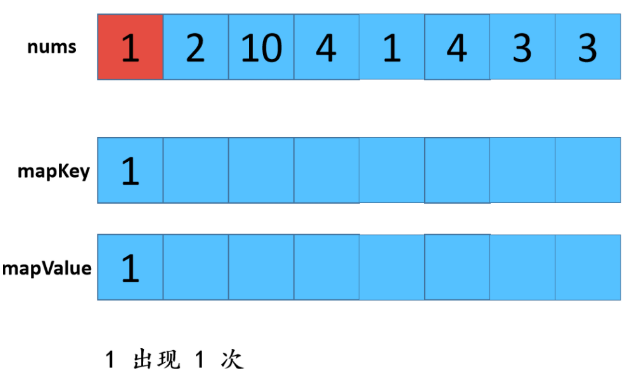
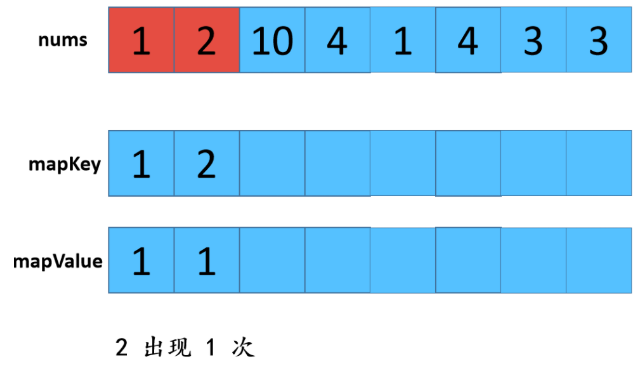
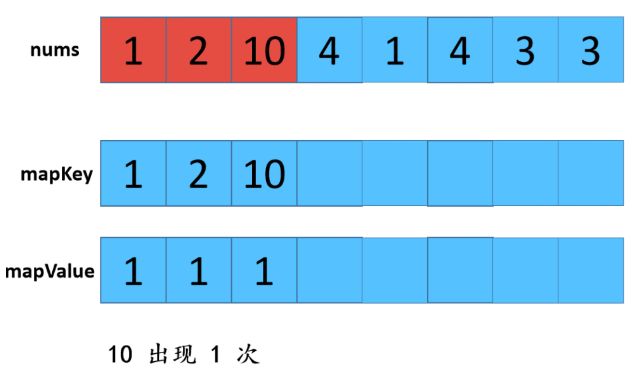
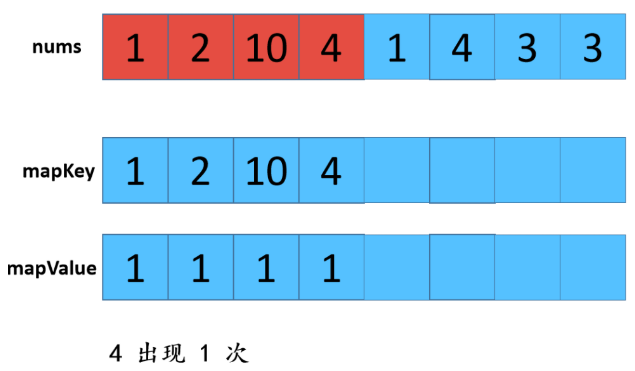
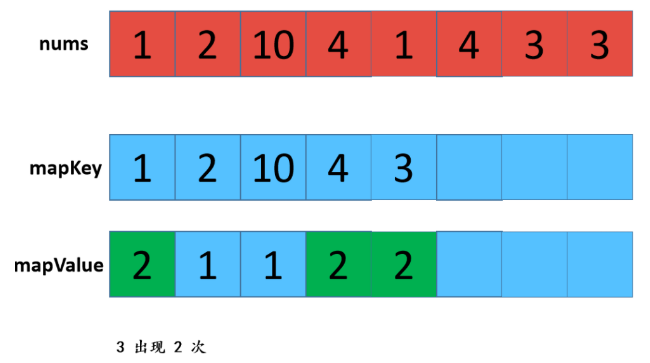
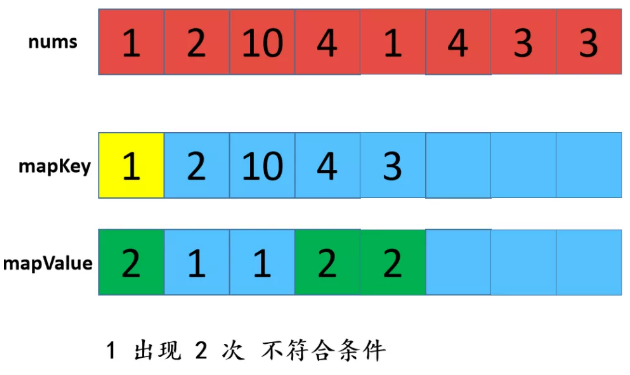
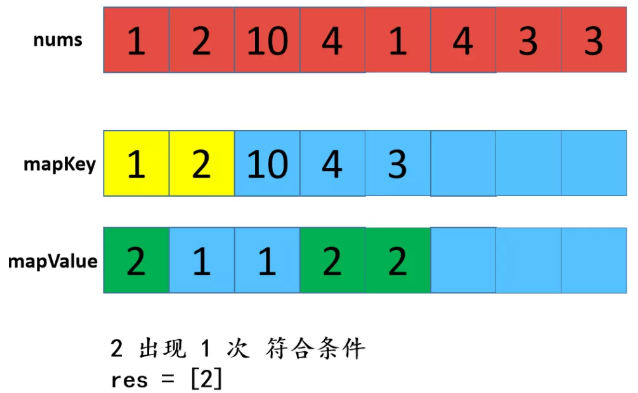
代码实现
class Solution {
public int[] singleNumbers(int[] nums) {
Map
拔高优化

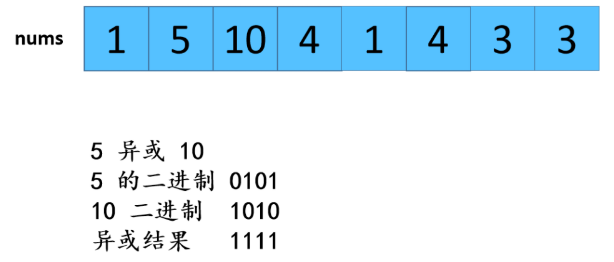

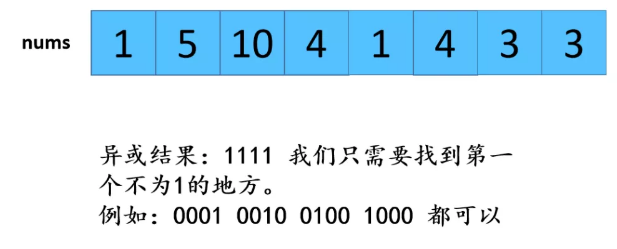



详细思路
代码实现
class Solution {
public int[] singleNumbers(int[] nums) {
//用于将所有的数异或起来
int k = 0;
for(int num: nums) {
k ^= num;
}
//获得k中最低位的1
int mask = 1;
while((k & mask) == 0) {//进行与操作
mask ;
}
int a = 0;//省去了两个数组的定义,直接在后序遍历中就进行异或操作
int b = 0;
for(int num: nums) {
if((num & mask) == 0) {
a ^= num;
} else {
b ^= num;
}
}
return new int[]{a, b};
}
}