【数据结构与算法】 通俗易懂讲解 二叉堆
2021-03-15 10:35
标签:结构 int 技术栈 服务器 详细介绍 alt 添加 整理 排列 堆(heap)又被为优先队列(priority queue)。尽管名为优先队列,但堆并不是队列。回忆一下,在队列中,我们可以进行的限定操作是dequeue和enqueue。dequeue是按照进入队列的先后顺序来取出元素。而在堆中,我们不是按照元素进入队列的先后顺序取出元素的,而是按照元素的优先级取出元素。 这就好像候机的时候,无论谁先到达候机厅,总是头等舱的乘客先登机,然后是商务舱的乘客,最后是经济舱的乘客。每个乘客都有头等舱、商务舱、经济舱三种个键值(key)中的一个。头等舱->商务舱->经济舱依次享有从高到低的优先级。 再比如,封建社会的等级制度,也是一个堆。在这个堆中,国王、贵族、骑士和农民是从高到低的优先级。 前面讲了二叉堆是完全二元树或者是近似完全二元树实现的堆结构,关于二叉树,详细介绍请见前面文章二叉搜索树(请戳我),二叉堆按照数据的排列方式可以分为两种:最大堆和最小堆。 二叉堆一般都通过"数组"来实现。数组实现的二叉堆,父节点和子节点的位置存在一定的关系。有时候,我们将"二叉堆的第一个元素"放在数组索引0的位置,有时候放在1的位置。当然,它们的本质一样(都是二叉堆),只是实现上稍微有一丁点区别。注意:本文二叉堆的实现统统都是采用"二叉堆第一个元素在数组索引为0"的方式! MaxHeap是最大堆的对应的类。它包括的核心内容是"添加"和"删除",理解这两个算法,二叉堆也就基本掌握了。下篇文章对它们进行介绍。 精心整理 | 历史干货文章目录 码农有道,为您提供通俗易懂的技术文章,让技术变的更简单! 【数据结构与算法】 通俗易懂讲解 二叉堆 标签:结构 int 技术栈 服务器 详细介绍 alt 添加 整理 排列 原文地址:https://blog.51cto.com/15006953/2552029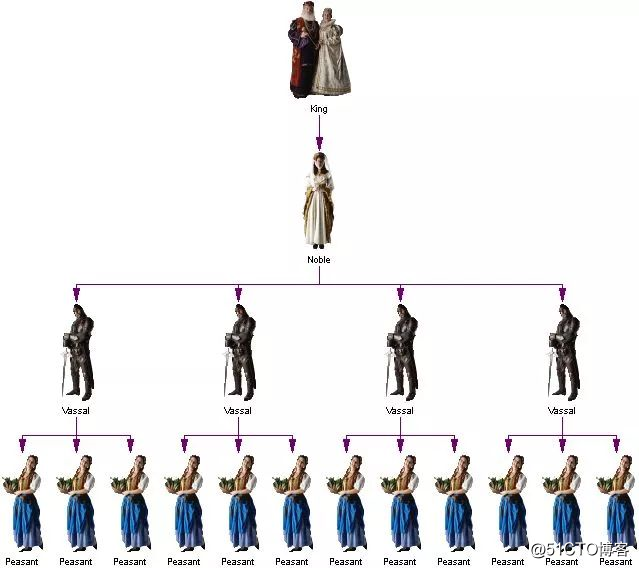
Linux内核中的调度器(scheduler)会按照各个进程的优先级来安排CPU执行哪一个进程。计算机中通常有多个进程,每个进程有不同的优先级(该优先级的计算会综合多个因素)。内核会找到优先级最高的进程,并执行。如果有优先级更高的进程被提交,那么调度器会转而安排该进程运行。优先级比较低的进程则会等待。“堆”是实现调度器的理想数据结构。
堆的一个经典的实现是完全二叉树(complete binary tree)。这样实现的堆成为二叉堆(binary heap)。二叉堆介绍-
最大堆:父结点的键值总是大于或等于任何一个子节点的键值;如下图左
最小堆:父结点的键值总是小于或等于任何一个子节点的键值。如下图右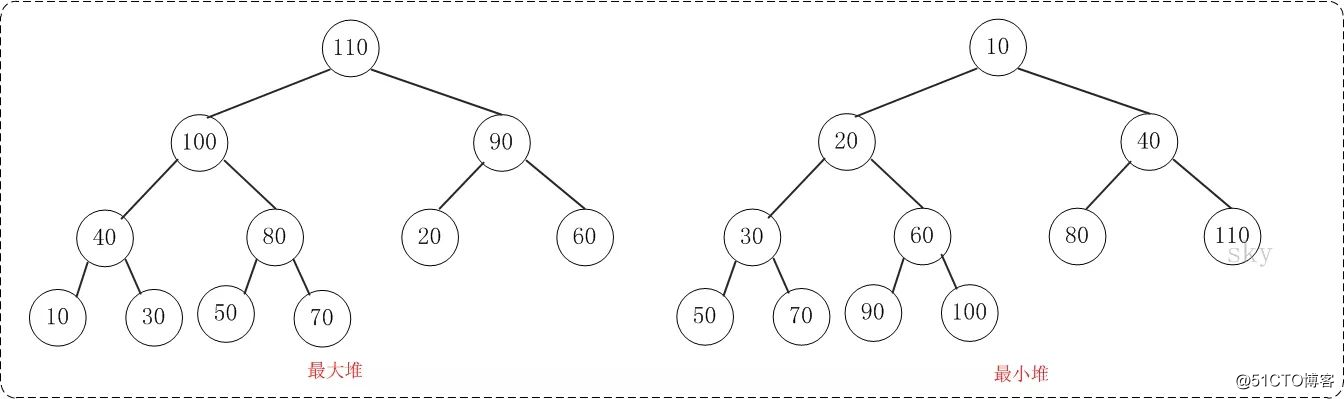
二叉堆定义及性质
假设"第一个元素"在数组中的索引为 0 ,对于父节点和子节点的位置有如下关系:
(1) 索引为i的左孩子的索引是 (2i+1);
(2) 索引为i的左孩子的索引是 (2i+2);
(3) 索引为i的父结点的索引是 floor((i-1)/2);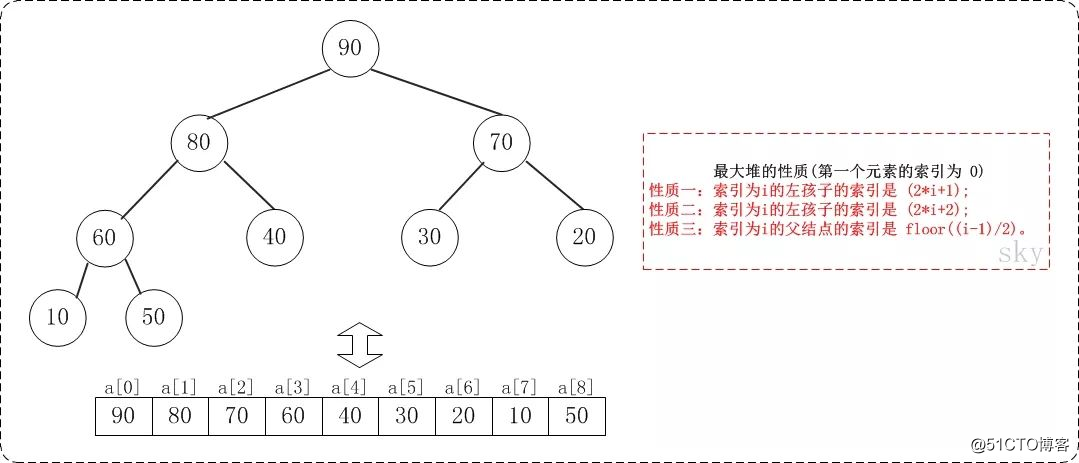
下面给出二叉堆的C++定义,为了通用性,定义成一个类模板:MaxHeaptemplate 推荐阅读:
【福利】自己搜集的网上精品课程视频分享(上)
【数据结构与算法】 通俗易懂讲解 二叉树遍历
【数据结构与算法】 通俗易懂讲解 二叉搜索树专注服务器后台技术栈知识总结分享
欢迎关注交流共同进步

码农有道 coding
文章标题:【数据结构与算法】 通俗易懂讲解 二叉堆
文章链接:http://soscw.com/index.php/essay/64922.html