打工人必会的快速幂算法详解
2021-03-21 22:28
标签:VID 转换 经典算法 计算 溢出 范围 哥哥 开始 str 快速幂是什么? 有多快? 用的多么? 下面来详细看看快速幂算法吧! 先看个问题再说: 首先问你一个问题,如果让你求 (2^10)%1000你可能会这样写: 熟悉的1024没问题,总共计算了10次。但是如果让你算 (2^50)%10000呢? 你可能会窃喜,小样,这就想难住我?我知道int只有32位,50位超出范围会带来数值越界的异常,我这次可以用long,long有64位呢! 计算50次出了结果正当你暗暗私喜的时候又来了一个要命的问题:让你算 (2^1e10)%10000 且不许你用Java大数类,你为此苦恼不知所措。这时bigsai小哥哥让你百度下取模运算,然后你恍然大悟,在纸上写了几个公式: 你还算聪明一眼发现其中的规律: 凭借这个递推你明白:每次相乘都取模。机智的你pia pia写下以下代码,却发现另一个问题:怎么跑不出来? 咱们打工人需要对计算机运行速度和数值有一个大致的概念。循环体中不同操作占用时间不同,所以当你的程序循环次数到达1e6或1e7的时候就需要非常非常小心了。如果循环体逻辑或者运算较多可能非常非常慢。 机智的你不甘失败,开始研究其数的规律,将这个公式写在手上、膀子上、小纸条上。吃饭睡觉都在看: 然后你突然发现其中的奥秘,n次幂可以拆分成一个平方计算后就剩余n/2的次幂了: 现在你已经明白了快速幂是怎么回事,但你可能有点上头,还是给我讲了很多内容: 至于快速幂已经懂了,我们该怎么实现这个算法呢? 说的不错,确实有递归和非递归的实现方式,但是递归使用的更多一些。在实现的时候,注意一下奇偶性、停止条件就可以了,奇数问题可以转换为偶数问题: 这里,递归的解法如下: 非递归实现也不难,控制好循环条件即可: 对于非递归你可能有点模糊为啥偶数情况不给res赋值。这里有两点: 如果还是不懂,可以用这个图来解释一下: 你以为这就结束了?虽然快速幂主要内容就是以上内容,但是总有很多牛人能够发现很有趣的规律—矩阵快速幂。如果你没听过的话建议仔细看看了解一下。 大家都知道斐波那契数列: 的规则: 前几个斐波那契的数列为:0, 1, 1, 2, 3, 5, 8, 13, 21, 34, … 斐波那契从递推式就可以看出是指数级别的增长,所以稍微多几个数字就是爆炸式增长,所以很多时候也会要求最后几位的结果。有了前面模运算公式溢出就不成问题,但n如果非常非常大怎么快速计算就成了一个新的问题。 我们看下面一组公式: 如果那f(n)和f(n-1)放到一个矩阵中(一行两列): 答案是存在规律的,看上面的公式知道 所以现在你可以知道它的规律了吧,这样一直迭代到f(2),f(1)刚好都为1,所以这个斐波那契的计算为: 而这个矩阵有很多次幂,就可以使用快速幂啦,原理一致,你只需要写一个矩阵乘法就可以啦,下面提供一个矩阵快速幂求斐波那契第n项的后三位数的模板,可以拿这个去试一试poj3070的题目啦。 这篇到这里就肝完啦,其实快速幂的内容还不止这么多,尤其是矩阵快速幂,会有着各种巧妙的变形,不过跟数学有一些关系,这年头,不会点算法、不会点数学真的是举步维艰。所以大家要对本篇内容好好吸收,让我那么久的努力发挥出作用。 如果有疑问不懂得欢迎私聊我讨论。也希望大家点个在看,您的支持是我努力的不断动力。 关注bigsai,回复bigsai领取干货资源,下次再见,打工人! 打工人必会的快速幂算法详解 标签:VID 转换 经典算法 计算 溢出 范围 哥哥 开始 str 原文地址:https://www.cnblogs.com/bigsai/p/13896172.html前言
快速幂介绍
初探
int va=1;
for(int i=0;ilong va=1;
for(int i=0;i(a + b) % p = (a % p + b % p) % p (1)
(a - b) % p = (a % p - b % p ) % p (2)
(a * b) % p = (a % p * b % p) % p (3)
a ^ b % p = ((a % p)^b) % p (4)
(a * b) % p = (a % p * b % p) % p (3)
(2*2*2···*2) %1e10=[2*(2*2···*2)]%1e5=(2%1e5)*(2*2···*2%le5)%1e5
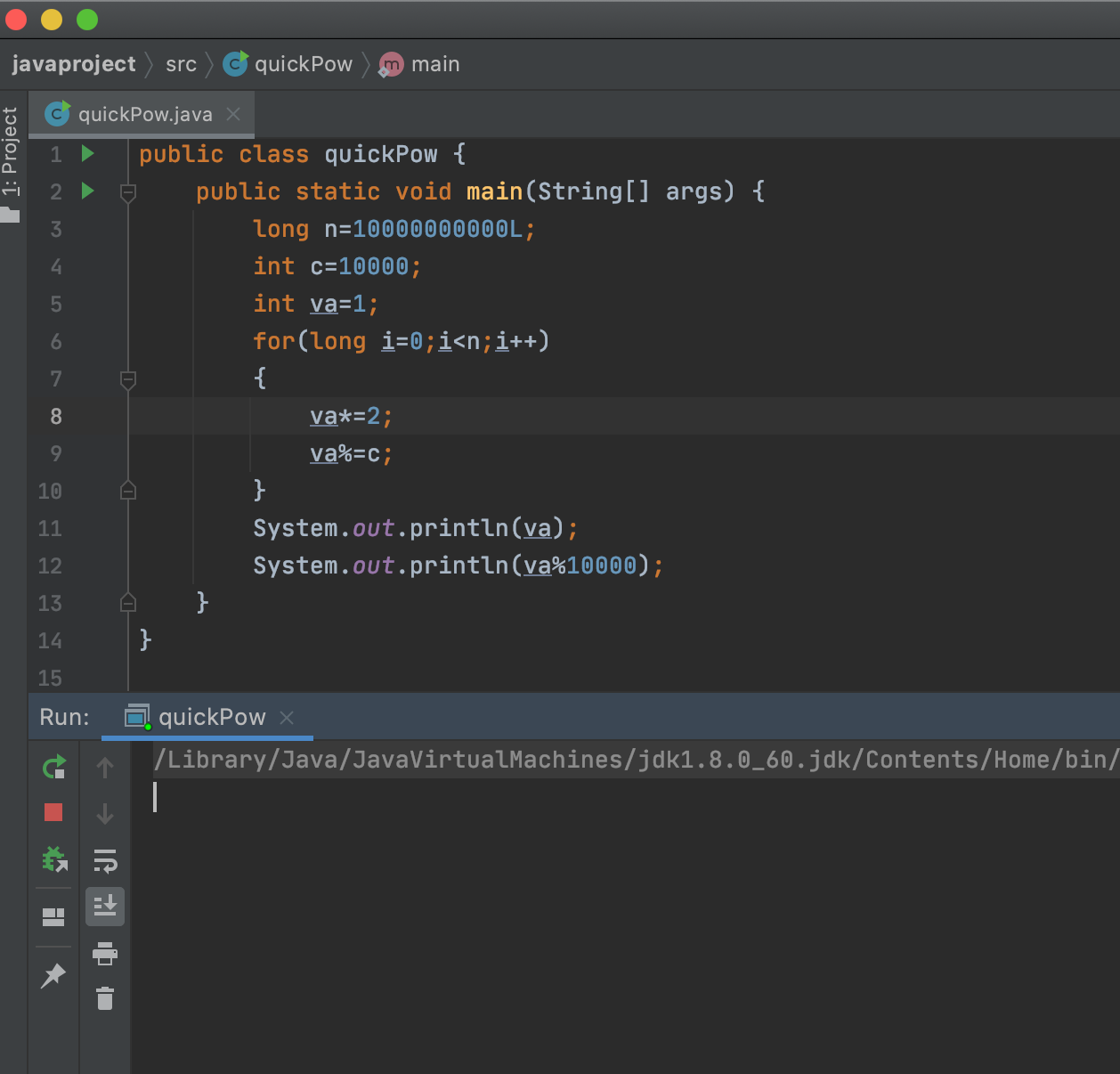
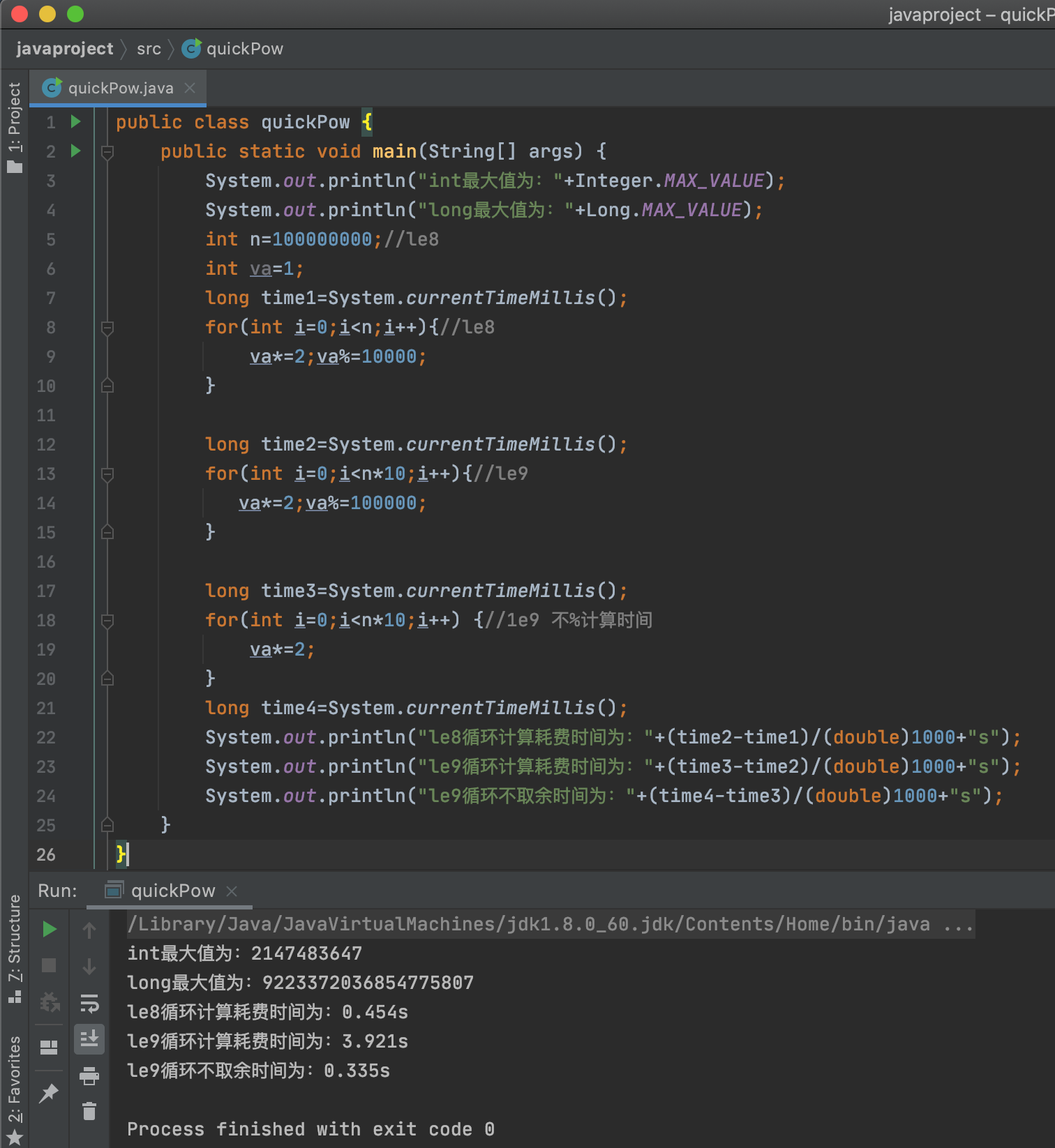
快速幂探索


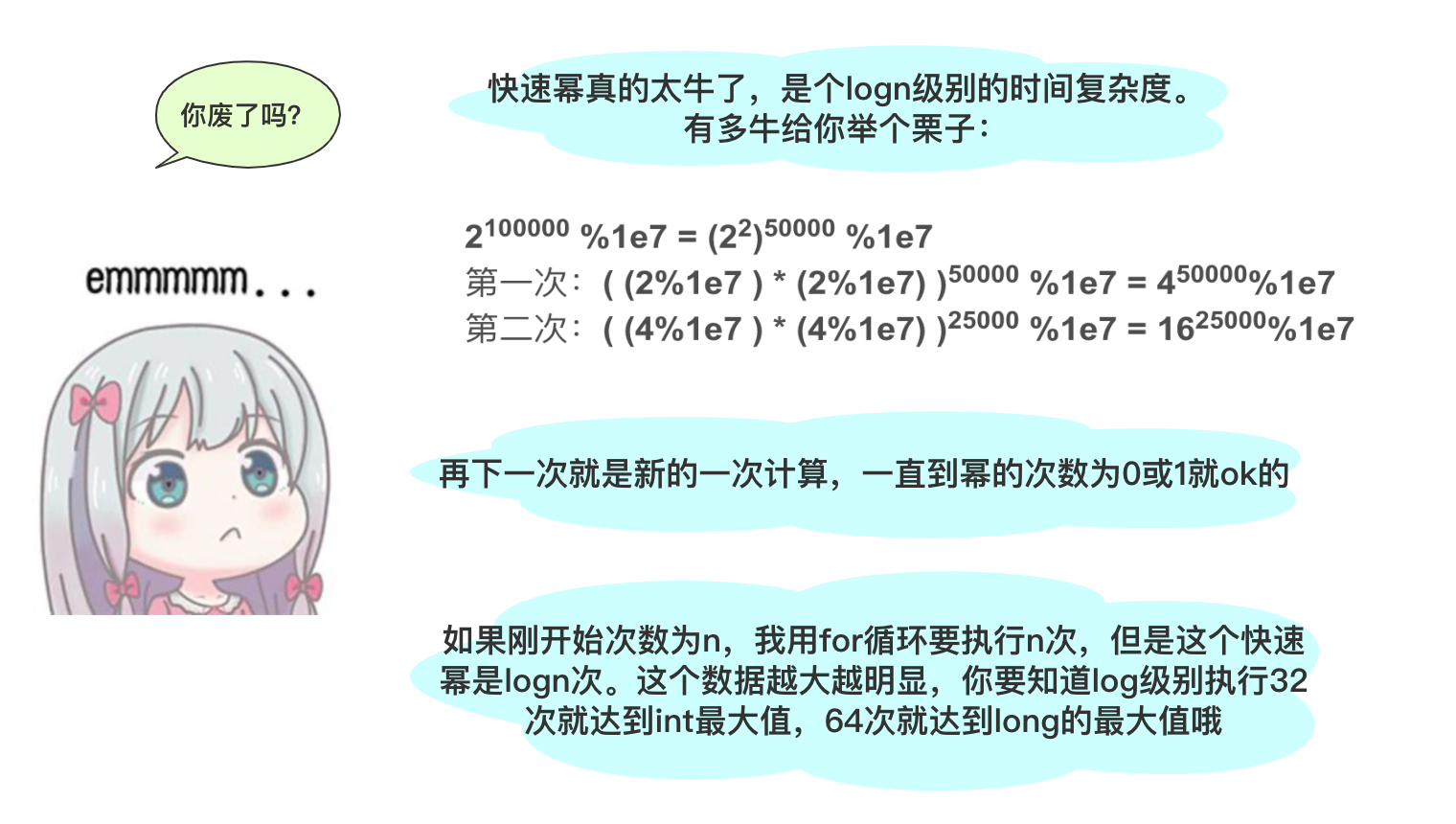
快速幂实现

2*2*2*2*2=2 * (2*2*2*2) 奇数问题可以转化为偶数问题。
long c=10000007;
public long divide(long a, long b) {
if (b == 0)
return 1;
else if (b % 2 == 0) //偶数情况
return divide((a % c) * (a % c), b / 2) % c;
else//奇数情况
return a % c * divide((a % c) * (a % c), (b - 1) / 2) % c;
}
//求 a^b%1000000007
long c = 1000000007;
public long divide(long a, long b) {
a %= c;
long res = 1;
for (; b != 0; b /= 2) {
if (b % 2 == 1)
res = (res * a) % c;
a = (a * a) % c;
}
return res;
}

矩阵快速幂
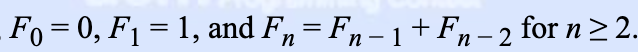
f(n+1) = f(n) + f(n-1)
f(n) = f(n)
[f(n+1),f(n)] 能否找到和[f(n),f(n-1)]之间的什么规律呢?[f(n+1),f(n)]
=[f(n)+f(n-1),f(n)]
[1 1]
=[f(n),f(n-1)] *
[1 0]
[1 1] [1 1]
=[f(n-1),f(n-2)]* *
[1 0] [1 1]
=·······
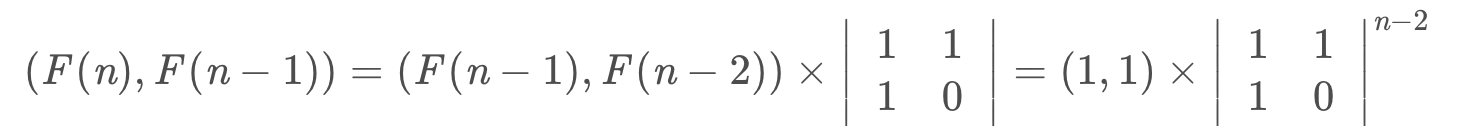
public int Fibonacci(int n)
{
n--;//矩阵为两项
int a[][]= {{1,1},{1,0}};//进行快速幂的矩阵
int b[][]={{1,0},{0,1}};//存储漏单奇数、结果的矩阵,初始为单位矩阵
int time=0;
while(n>0)
{
if(n%2==1)
{
b=matrixMultiplication(a, b);
}
a=matrixMultiplication(a, a);
n/=2;
}
return b[0][0];
}
public int [][]matrixMultiplication(int a[][],int b[][]){//
int x=a.length;//a[0].length=b.length 为满足条件
int y=b[0].length;//确定每一排有几个
int c[][]=new int [x][y];
for(int i=0;i结语

