扫描线算法

标签：覆盖   连续   push   ==   扫描   can   space   png   image   

ioi1998 Picture
在一个平面上放置一些矩形，所有的边都为垂直或水平。每个矩形可以被其它矩形部分或完全遮盖，所有矩形合并成区域的边界周长称为轮廓周长。
要求：计算轮廓周长。
数据规模：
0≤矩形数目坐标数值为整数，范围是[-10000，10000]。
Input
第一橫列是牆上所貼的長方形圖片總數。之後每一橫列是一個長方形的左下角與右上角的整數座標。各座標的x值在前，y值在後。
Output
應有一非負整數，即為長方形圖片聯集體的總周長
Sample Input
7
-15 0 5 10
-5 8 20 25
15 -4 24 14
0 -6 16 4
2 15 10 22
30 10 36 20
34 0 40 16
Sample Output
228

扫描线算法:
将线段放到线段树上，每个矩形两条竖线，两条横边，情况是一样的。
对于两条竖边，左边的为入边，右边的为出边。
遇到左边的边，染色次数tim为1.投到线段线上。
线段树上相应的区间当染色次数tim为0变1，或者1变成0时，才统计结果。
对于下图
先将1，2这两条统计进来
再加入蓝色这个长条矩形时
对于3条边，直接加上，因为染色次数tim是从0变成1
对于4条边，不能加入，因为染色次数tim是从1变成2
对于5条边，直接加上，因为染色次数tim是从0变成1
对于6条边，不能加入，因为染色次数tim是从1变成2
对于7条边，直接加上，因为染色次数tim是从0变成1
下面讲下染色次数tim的变化
当对某条线段进行染色次数tim变化时，要检查下其是否是一条“统一”的线段
即这条线段的子线段被染色的次数是一样的。例如
加入两个小矩形后,[a,b]是不连续的

当长竖矩形加入后
对于整条线段[a‘,b]，它开始是不能处理的，因为对应的线段状态不统一
于是递归下去
到了[a‘,c‘]这一段是能处理的，tim从0变1
到了[c‘,d‘]这一段是能处理的，tim从1变2
于是对于[a‘,d‘]这一段的状态也是不统一的
当处理线段[a‘‘,d‘‘]时也是要分开进行处理的
即分别处理[a‘‘,c‘‘]让线段的染色次数tim从1变成0，进行累加
再处理[c‘‘,d‘‘]让线段的染色次数tim从2变1，不进行累加
一句话概括就是：
将一条线段分成若干段，每段的tim代表被染色的次数。只有次数一样时这一段的状态就是统一的（即不为-1).否则各有各的染色次数。只有当染色次数从0变1，或者1变0时才计数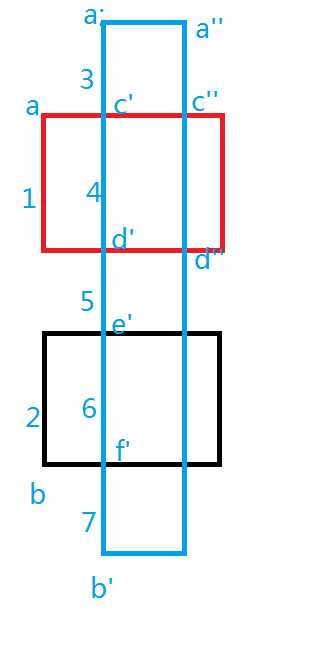

//先将每条边抽离出来，例如对于(a,b),(c,d)两个点组成的矩形，其中(a,b)是左下角,(c,d)是右上角
//则有一条竖着的进入边覆盖区间(b,d),它是在x轴上a点时进入的
//其对应的出边也是覆盖(b,d),它是在x轴上c点时离开的
//将所有竖边按x轴上的顺序升序排好，如果值一样，则进边在前，出边在后
//然后不断加边进去，将对应的区间从0变成1时，或1变成0时统计长度，其它值的变化时并不统计长度
 
#include
#include
using namespace std;
const int N=1e4;
int tim[10*N],lazy[10*N],ans;
struct momo
{
    int begin,end,mark,place;
};
bool cmp(momo x,momo y)
{
    if(x.place!=y.place)
	    return x.placey.mark;
//按坐标轴从小到大,如果坐标轴一样则进入边在前，出去的边在后面 
}
void pushdown(int num)
{
    if(lazy[num])
    {
        if(tim[num]!=-1)//如果整个线段状态是统一的，即要么全覆盖，要么全没有覆盖 
		    tim[num]+=lazy[num];
        lazy[num*2]+=lazy[num];
        lazy[num*2+1]+=lazy[num];
        lazy[num]=0;
    }
}
void change(int num,int l,int r,int x,int y,int v)
{
    if(l>=x&&rmid)
	    change(num*2+1,mid,r,x,y,v);
    if(tim[num*2]==tim[num*2+1]) //统一一下标计 
	    tim[num]=tim[num*2];
    else
        tim[num]=-1;
}
momo high[N+100],wide[N+100];
int main()
{
    int n;
    scanf("%d",&n);
    for(int i=1;i

扫描线算法

标签：覆盖   连续   push   ==   扫描   can   space   png   image   

原文地址：https://www.cnblogs.com/cutemush/p/13339216.html