图的最短路径(Dijkstra)(Floyd),拓扑排序,生成树代码
标签:void 邻接矩阵 i++ ++ main 代码 sele oid include
使用邻接矩阵存储加权图,无穷大使用常数MAXLEN代表,然后使用Dijkstra方法求取最短路径
1 #include 2
3 #define MAXLEN 1000
4 int cost[7][7];
5 int dist[7];
6
7 void creategraph(int* node,int num)
8 {
9 int from;
10 int to;
11 int i;
12 for(i = 0;i )
13 {
14 from = node[i*3];
15 to = node[i*3+1];
16 cost[from][to] = node[i*3+2];
17 }
18 }
19
20 void shortestpath(int begin,int num)
21 {
22 int selected[7];
23 int min;
24 int s;
25 int i,j;
26
27 for(i = 2;i )
28 {
29 selected[i] = 0;
30 dist[i] = cost[begin][i];
31 }
32 selected[begin] = 1;
33 dist[begin] = 0;
34 printf("顶点1 2 3 4 5 6\n");
35 for(j = 1;j )
36 printf(" %4d ",dist[j]);
37 printf("\n");
38 for(i = 1;i 1;i++)
39 {
40 min = MAXLEN;
41 for(j = 1;j )
42 if(min > dist[j] && selected[j] == 0)
43 {
44 s = j;
45 min = dist[j];
46 }
47 selected[s] = 1;
48 for(j = 1;j )
49 {
50 if(selected[j] == 0 &&
51 dist[s] + cost[s][j] dist[j])
52 dist[j] = dist[s] + cost[s][j];
53 printf(" %4d ",dist[j]);
54 }
55 printf("\n");
56 }
57 }
58
59 int main()
60 {
61 int node[7][3] = {
62 { 1, 2, 35},
63 { 2, 3, 45},
64 { 2, 4, 30},
65 { 3, 5, 25},
66 { 4, 5, 45},
67 { 4, 6, 130},
68 { 5, 6, 100},
69 };
70 int i,j;
71
72 for(i = 1;i 6;i++)
73 for(j = 1;j 6;j++)
74 cost[i][j] = MAXLEN;
75 creategraph(node,7);
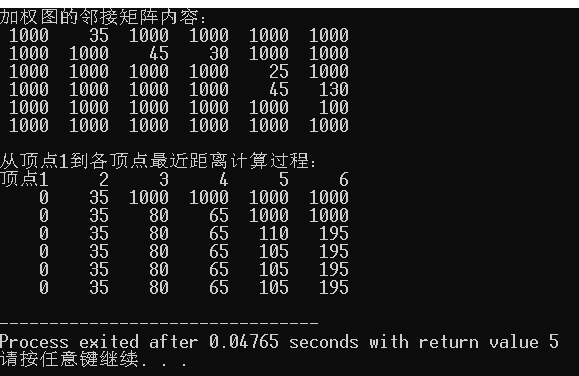
76 printf("加权图的邻接矩阵内容:\n");
77 for(i = 1;i 6;i++)
78 {
79 for(j = 1;j 6;j++)
80 printf(" %4d ",cost[i][j]);
81 printf("\n");
82 }
83 printf("\n从顶点1到各顶点最近距离计算过程:\n");
84 shortestpath(1,6);
85 }
图的最短路径(Dijkstra)(Floyd),拓扑排序,生成树代码
标签:void 邻接矩阵 i++ ++ main 代码 sele oid include
原文地址:https://www.cnblogs.com/hulianxingkong/p/14224228.html
评论
