用Python实现最大堆
2021-06-11 10:06
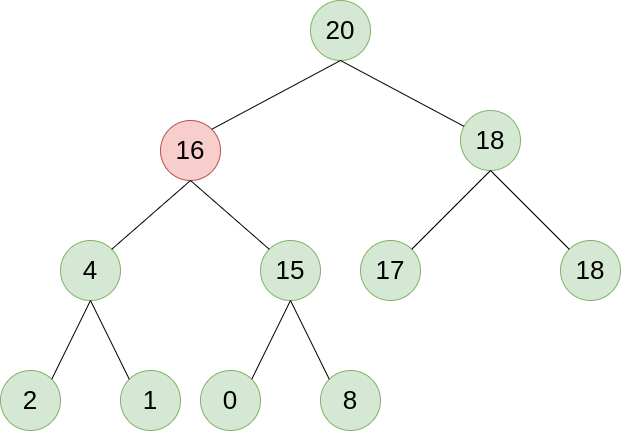
标签:最小堆 pop org shu 它的 ext sift rem 定义 本文的内容是如何通过二叉树实现一个最大堆, 实现原理方面参考了这篇文章. 堆的本质就是一颗二叉树, 这颗二叉树必须具备以下两个性质: 1). 对于最大堆来说, 二叉树根节点的值不小于任何子节点, 其所有子树也符合这一特征, 最小堆则相反; 2). 堆是一颗完全二叉树, 除了底层外, 所有层都尽可能地填满, 底层元素从左到右排列. 上图就是一个最大堆的二叉树, 基于特性1我们可以得知, 这颗二叉树从任意叶子节点到根节点的路径一定是一个递增序列, 最大值为根节点. 因此, 当我们需要最大值时, 取出根节点的值就行了. 当我们新添加了一个叶子节点之后, 为了维护二叉树的有序性, 我们可以让这个叶子节点向顶端移动, 如下图所示: 我们插入节点16后, 将这个节点的值与其父节点进行比较, 大于父节点则二者交换, 持续这个操作直到不大于父节点或没有父节点为止, 这样, 我们就在插入元素之后, 仍然保持了二叉树的有序性. 弹出节点同理, 将底层最后一个叶子节点取出填入空缺, 然后根据值的大小让这个节点往下移动就行. 因此, 堆在保证内部有序性的前提下, 可以做到在O(k)的时间内插入和弹出元素, k为二叉树的高度. 这也就是为什么堆的二叉树必须是完全二叉树: 在这种情况下k最小, 为log n. 因此, 堆的插入和弹出都只需要O(log n)的时间复杂度, 可以高效地获取最大值/最小值. 由于堆是一颗完全二叉树, 因此我们可以用一个列表来储存这颗二叉树的值: 如上图所示, 我们用列表从上到下, 从左到右记录了二叉树的所有节点. 二叉树节点右边的蓝色数字是它在列表中的索引. 因此我们可以得知, 对于一个在列表中索引为n的节点, 它的父节点索引为(n-1)//2, 它的左右子节点索引为n*2+1和n*2+2, 如果索引值溢出, 说明没有对应的父节点或子节点. 这样, 我们就通过列表储存了这颗完全二叉树的信息. 基于以上的分析, 我们先定义一个Heap类: 这部分好像太简单了, 我实在讲不出来什么: 说白了, 当我们push一个元素时, 首先把这个元素放到列表的末端, 这相当于在完全二叉树上新建了一个叶子节点. 然后, 调用siftup方法让这个节点一直和父节点比较, 大于父节点就上浮, 直到它到达合适的位置. 这样就维护了二叉树的有序性. 弹出元素的原理和插入元素大同小异: 我们将根节点的元素弹出后, 取出最后一个叶子节点作为根节点(避免破坏完全二叉树的结构), 然后让这个节点与子节点比较, 下沉到合适的位置就行. 有两点需要注意一下: 首先, 最大元素处在列表的头部, 弹出的时间复杂度是O(n), 因此我们可以把头部元素和尾部元素交换后, 删除尾部元素. 然后, 大部分节点都有两个子节点, 我们应该让更大的那个节点上浮, 这样才能保证二叉树的有序性. 基于以上两点, 弹出元素的代码如下: 简单对我们创建的Heap类进行测试: 结果如下: 用Python实现最大堆 标签:最小堆 pop org shu 它的 ext sift rem 定义 原文地址:https://www.cnblogs.com/q1214367903/p/14220949.html一. 堆的数据结构
1. 数据结构分析
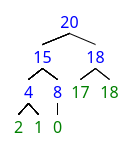
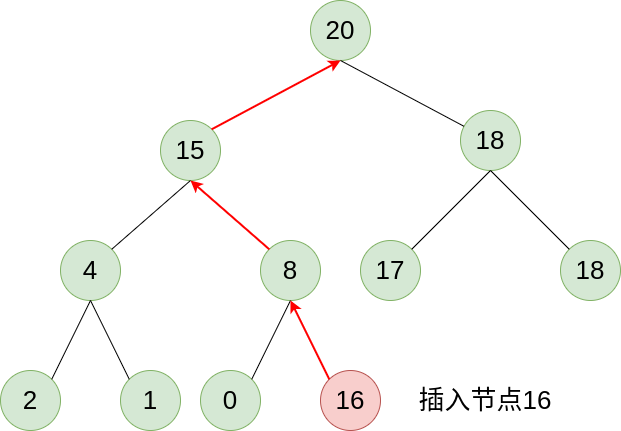 ->
->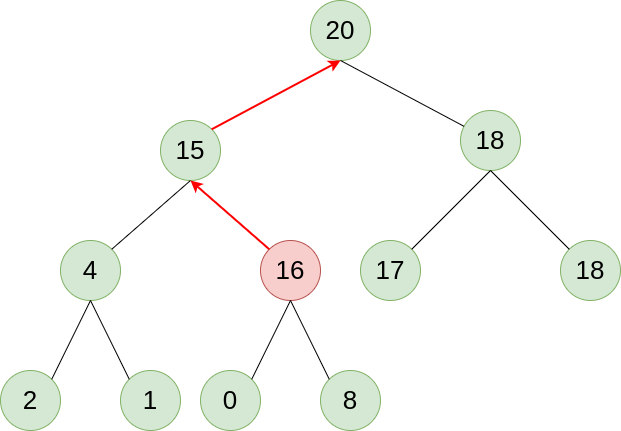 ->
->
2. 通过列表实现二叉树
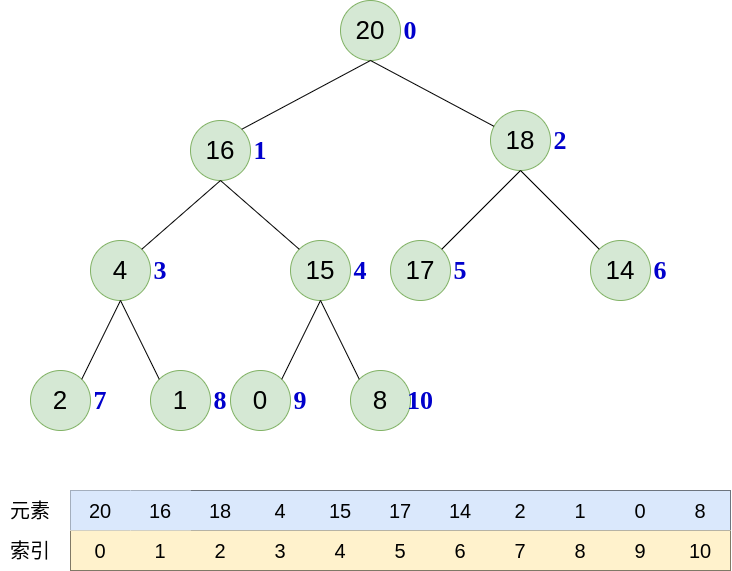
class Heap:
def __init__(self, nums: [int] = None) -> None:
self.cache = []
if nums is not None:
for num in nums:
self.push(num)
def __len__(self) -> int:
return len(self.cache)
def __bool__(self) -> bool:
return len(self) > 0
def __repr__(self) -> str:
return f‘heap({self.cache})‘
@property
def largest(self) -> int:
if not self.cache:
raise Exception(‘Empty heap‘)
return self.cache[0]
def show(self) -> None:
# 调用这个函数绘制一颗二叉树出来,DEBUG用
height = int(math.log2(len(self))) + 1
for i in range(height):
width = 2 ** (height - i) - 2
print(‘ ‘ * width, end=‘‘)
blank = ‘ ‘ * (width * 2 + 2)
print(
blank.join([‘{: >2d}‘.format(num) for num in self.cache[2 ** i - 1:min(2 ** (i + 1) - 1, len(self))]]))
print()
def _swap(self, i: int, j: int) -> None:
# 这个函数用于交换二叉树的两个节点
self.cache[i], self.cache[j] = self.cache[j], self.cache[i]
二. 插入元素
def push(self, num: int) -> None:
self.cache.append(num)
self._siftup(self.size - 1)
def _siftup(self, i: int) -> None:
while i > 0:
parent = (i - 1) >> 1
if self.cache[i] self.cache[parent]:
break
self._swap(i, parent)
i = parent
三. 弹出元素
def pop(self) -> int:
largest = self.largest
self._swap(0, len(self) - 1)
self.cache.pop()
self._siftdown(0)
return largest
def _siftdown(self, i: int) -> None:
while i * 2 + 1 len(self):
smaller = i
if self.cache[i * 2 + 1] > self.cache[smaller]:
smaller = i * 2 + 1
if i * 2 + 2 and self.cache[i * 2 + 2] > self.cache[smaller]:
smaller = i * 2 + 2
if smaller == i:
return
self._swap(i, smaller)
i = smaller
四. 总结
nums = list(range(14))
random.shuffle(nums)
heap = Heap(nums)
heap.show()
heap.push(100)
print(‘插入100‘)
heap.show()
heap.pop()
print(‘弹出堆顶元素‘)
heap.show()
for _ in range(100):
num = random.randrange(100)
nums.append(num)
heap.push(num)
assert max(nums) == heap.largest
nums.remove(heap.pop())
print(‘所有测试通过!!!‘)
